[Gym Contest Editorial] Egyptian Collegiate Programming Contest (ECPC 2015)

#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Note: All complexities mentioned in this editorial are per test case.

A: Arcade Game

Let perm be the number of permutations for the digits of n.
First, sort all these permutations in decreasing order and give each permutation a rank (0 is the largest permutation, 1 is the second largest and so on).
ans[0] = 0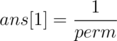
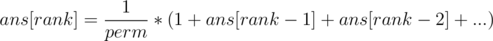
$\text{[math]}$
$\text{[math]}$
find the rank of n and print it's value from the array.

Note: the relation mentioned above can be reduced to:

$\text{[math]}$
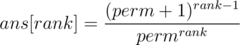
Which could be written as (to avoid overflow):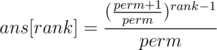
$\text{[math]}$

Complexity: O(rank)

B: Unlucky Teacher

There are two ways for an answer to a question to be unique:
1) this question was answered correctly in one of the papers.
2) this question was answered incorrectly for three different choices.
So, for every question, we maintain a set of the possible answers for this question. Initially, the set of every question is {A, B, C, D} , when we get a wrong answer for this question, we remove that answer from the set. When we get a correct answer for this question, we remove all the answers except this one from the set.
Now, for every question, if the set contains one answer, print it, otherwise print '?'.
Complexity: O(MQ).

C: Connecting Graph

In this solution, I am going to use a more basic version of DSU, which is storing for each component all the elements that it includes, and merging two components is done by choosing the smaller component (i.e. the one with a smaller number of elements). And then moving its elements one by one to the other (big) component.

Solution:

We are going to use a DSU that has two kinds of elements, Nodes and type B Queries.

In the beginning, each component has a single node and all the queries of type B that involve it.

Then let’s process the queries of type A in their given order, for each query we’ll merge components of u, v using the mentioned above method, but for each type B Query element we have to cases:

1) This current type A query is the earliest query which connects the nodes in Query B. Then both of its nodes will belong to one component after merging, (it can be checked in O(1)), thus this Type B query is answered, we’ll store it’s answer in some array and then delete it from the component.

2) Its nodes aren’t connected yet, so we should add it normally to the component.

Complexity: O((N + Q)log(N + Q))

D: Frozen Rivers

Traverse the tree using DFS while storing the time needed to reach each node in an array, let us call it T.
T[1] = 1
If we are in node v:
1) we find the length of the shortest edge from v to one of it's sons, let us call it shortest.
2) we go through every son u_i of v, T[u_i] = T[v] + shortest + (len[v][u_i] - shortest) * 2 (since the water will flow for shortest seconds at a rate of 1 unit/s. and then it will slow down to 0.5 unit/s for the rest of the distance).
Now, we sort the leaves of the tree by the time needed to reach each of them, and answer the queries by binary search or 2-pointers.
Complexity: O(nlog(n))

E: Palmyra

Note:
1) A number L ends in x trailing zeros when written in base-6, if it could be written as:
L = 6^x * h (h is a number that is not divisible by 6)
L = 2^x * 3^x * h
2) If a number H can be written as H = 2^a * 3^b * h , H will have min(a, b) trailing zeros when written in base-6.

In this problem , we need to maximize x which can be done by DP:
DP[i][j][k] is the maximum x such that there is a path that starts in (1,1) and ends in (i,j) and the product of the numbers along the path is divisible by 2^x * 3^k
DP[i][j][k] = max(dp[i - 1][j][k - n3], dp[i][j - 1][k - n3]) + n2
Where n2, n3 are the number of times the power of the current stone can be divided by 2,3 respectively.
The answer is the maximum of min(k, dp[n][m][k]) for all k

Complexity:
The length of the path is n + m - 1
Each stone power can be divided by 3 at most log₃(a[i][j]) times.
So the maximum k is log₃(max(a[i][j])) * (n + m - 1)
Total Complexity: O(nm(n + m)log₃(max(a[i][j])))

F: Geometry

If H = W the shape is a square, otherwise it's a rectangle
Complexity: O(1)

G: It is all about wisdom

We can find the minimum wisdom value needed to go from 1 to N with cost <K by binary search.

To check if a wisdom value x is enough to go from 1 to N with cost <K, we can use dijkstra by considering edges that need wisdom value ≤ x.
Total Complexity: O(mlog(n)log(m))

H: Tonight Dinner

1) There is always a way to assign seats for the 2 tables without having any intersections between paths, by just reverse the order of the guests in the seats.

The problem is equivalent to given 2 circular permutations, determine the least number of swaps between adjacent elements to turn one permutation into the reverse of the other.

There are at least 2 adjacent elements with crossing paths. If A, B are 2 not adjacent corners and their paths are crossing then there is a corner C between them where its path intersects with A or with B.

We can remove one intersection by swapping A and B.

To calculate the number of swaps of adjacent elements to turn sequence A to sequence B, you can try all rotations of B with A.

We can assume without loss of generality that A is the first permutation (1234…) then we can define displacement vector of B with A as V[i] = B[i]–i

Then count the crosses between all pairs by comparing the old and new place for each guest (if guest g₁ was right to guest g₂ and after the movement he is on the left, or vice versa, then there is a crossing)

To handle circular movement, try all rotations of vector V[i]

print the minimum number of crossings.

Complexity: O(n⁴)

I: Salem

Go through all pairs of integers, convert them to binary, and calculate the hamming distance between them, and return the maximum.
Calculating the hamming distance between x and y:

int dist=0;
while(x>0 && y>0)  
{
    if (x%2!=y%2) dist++;
    x/=2,y/=2;
}

Or you can count the number of bits in x xor y for a shorter code:
dist=__builtin_popcount(x^y)

Complexity: O(n²log(n))

J: Game

Observation: After every move, the length of the string is halved. Therefore, after log(n) moves, the game will end.
We can try all possible moves. A state with string s is called winning if one of the following is true:
1) |s| = 1, s[0] is a vowel, and it's Salah's turn.
2) |s| = 1, s[0] is not a vowel, and it's Marzo's turn.
3) |s| > 1 and one of the 2 possible moves leads to a losing state.

If the initial string is a winning state, Salah wins, otherwise Marzo wins.
The complexity of this solution can be proved to be O(nlog(n)) (n is the length of the initial string)

Proof:
For each state with string s, we need O(|s|) to get s1, s2 (the result of applying LEFT and RIGHT moves on string s respectively)
Let f(i) be the number of strings(states) we might end up with after finishing i moves. f(i) = 2ⁱ
Let g(i) be the length of the string we end up with after finishing i moves. 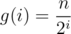$\text{[math]}$
The total complexity is 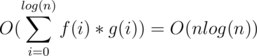$\text{[math]}$

K: PhD Math

First calculate the first n decimal digits of $\text{[math]}$ and store them in an array s
Let DP[i][j] be the number of substrings of s that ends at i and the value of this substring mod p = j.
If we have a substring that ends at i - 1 and it's value mod p = j then we can extend it to i , and the value mod p will become:
(j * 10 + s[i])modp
So we add the value of DP[i - 1][j] to DP[i][(j * 10 + s[i])%p]
and since we can start a new substring at i , we add 1 to DP[i][s[i]%p]
The answer is: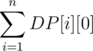
$\text{[math]}$

In order to use less memory, we can notice that every value in DP[i] depends only on some values from DP[i - 1] , so we only store DP[i] and DP[i - 1]

Complexity: O(n * p)

L: Candy Jars

Notes:
1) If all jars have 1 to N - 1 candies, that is a losing state.

2) If there is at least one jar that has N to N(N - 1) candies, that is a wining state.

3) If all jars have N(N - 1) + 1 to N(N - 1) + (N - 1) candies that is a losing state because any move will put N to N(N - 1) candies in one jar.

4) Adding N(N - 1) candies will not change the state.

So:

If candies c in all jars satisfy 1 ≤ c%N(N - 1) < N then this is a losing state (print Bob) else it is a wining state (print Alice)

Complexity: O(n)

M: Building Force Fields

After sorting all points by x coordinates.

It’s easy to show that optimal polyline for a group is the upper part of a convex hull (i.e. the upper polyline that starts from earliest x coordinate in the convex hull to the latest x coordinate).

So the optimal solution should divide consecutive points into groups after sorting.

If we can calculate the cost of creating a group from point i to j let’s name it C(i, j).

The problem is reduced to a classical DP problem.

DP[x] = min(DP[i] + C(i + 1, x)) : i < x - 1

Where DP[i] is the least cost to solve the problem for the first i points.

How to calculate C(j, i) ?

For each element i, start from i and go backwards while maintaining a stack that includes the points of the polyline, using the classic convex hull algorithm.

Total Complexity O(n²).

Comments (19)

Show archived | Write comment?

Alex7

9 years ago, # |

I'm the author of c and m. if you have any feedback please share it with me

→ Reply

llaugusty

9 years ago, # ^ |

about problem C. Can u give more detail? I use map for B queues but TLE on test 2.

RedNextCentury

You can store for each component, a vector that has all type B queries related to the nodes of this component

nnahas

+18

I am the author of problems K and H. Here is a more detailed explanation for problem H. Any question/comment is welcome. Some proofs and implementation details are still missing and I will later post an update to complete the missing parts.

The problem is essentially equivalent to the following: Given 2 circular permutations, determine the least number of swaps between adjacent elements to turn one permutation into the reverse of the other. To prove this equivalence, we need to prove 2 claims: 1)For every possible valid paths configuration C with number of intersections X , there is a sequence of swaps between adjacent elements of length X that turns one seating order into the reverse of the other. 2)For every sequence of swaps between adjacent elements of length X that turns one seating order into the reverse of the other, there is a corresponding valid paths configuration with number of intersections X.

To prove 1), we make the following observation: In any valid path configuration, if some two paths intersect, then at least two paths originating at adjacent locations intersect. To see that, imagine two paths, one originating at corner A and the other at corner B, and meeting at P. If A and B are not adjacent, there exists a corner C between A and B that belongs to the area ABP. In order to leave the area limited by the table and paths AP and BP and reach the dessert table, the path starting at C will have to intersect either AP or BP. We can repeat the procedure, proving the existence of intersecting paths whose origins form a narrower and narrower interval, and this procedure will stop only when the two intersecting paths have adjacent starting points. Now, assume we just swap the starting points and undo the crossing (making the path of the first continue along the old path of the second after the crossing and vice versa). We end up with a configuration with one less crossing. By repeating this procedure, we can remove all crossings by performing as many adjacent swaps as there are crossings.

To prove 2) just imagine a sequence of X concentric circles around the dinner table, with the order of the guests around each circle differing from the previous circle by exactly one adjacent swap, until we reach the outermost circle where the guests will be placed in the exact opposite clockwise order from that of the dessert table. By connecting a guest's successive positions on the concentric circle, we end up with a path configuration that has no more crossings than the number of steps in the swap sequence.

We still have to find an algorithm to determine the shortest sequence of adjacent swaps that will turn one circular permutation into the other.

To the best of my knowledge, the algorithm to solve this problem and its proof of correctness were first published in the following article: The complexity of finding minimum length generator sequences, Mark Jerrum, Theoretical Computer Science, 1985. The algorithm described in the paper doesn't exactly solve the problem of turning a circular permutation into another; Rather, it solves the problem of turning one linear permutation into another, when the allowed operations are swaps between adjacent elements and swapping the first element with the last. But, by trying all possible linear orders corresponding to the first circular permutation, we can reduce our problem to the one described in the paper. I will now try to explain the main ideas of the algorithm. First of all we need the concept of "displacement vector". In the context of linear permutations on n element, let S be the set containing all swaps between elements on adjacent indices, along with the swap between the first and last element. Assume we have two linear permutation P and P' and a sequence of swaps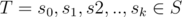 $\text{[math]}$ that will turn P into P'. When applying the sequence of swaps, if an element moves from index i to index i + 1 or from index n - 1 to index 0 we will say that this element moves clockwise, and if an element moves from index i to index i - 1 or from index 0 to index n - 1 we will say that this element moves anti-clockwise. let j be the index of an element x in P and let k be the index of x in P'. When the sequence T is applied to permutation P, element x might move clockwise at some steps and anti-clockwise at some others, but if the total number of clockwise moves for x is larger than the number of anti-clockwise moves, we will say that x traveled clockwise, otherwise we will say that x traveled anti-clockwise. We define the displacement vector d of sequence T as follows: the ith entry of the vector, d_i is the difference between the number of clockwise moves and the number of anti-clockwise moves that the ith element in P undergoes when T is applied. We now have to make some observations:

a)The sum of the entries of the displacement vector must necessarily be 0, because every a swapping operation is applied, one element goes clockwise and the other anti-clockwise.

b)Any optimal sequence T_opt cannot swap the same two elements with each other twice. Hence all entries of the displacement vector must be between 0 and n - 1.

c)If we denote the displacement vector by v, we have P_i = P'_{(i + v_i)modn}. This equality just expresses the fact that T takes the ith element in P to position (i + v_i)modn) in P'.

d)Given the displacement vector d of an optimal sequence T_opt, and the permutations P and P', it is possible to deduce the number of swaps in the sequence T without knowing T: if two elements travel past each other, there must be a swap that will involve them, and if they don't, then no swap will ever involve them, because otherwise a swap between those elements will occur twice, which would be redundant.For instance, assume d₂ = 3 and d₃ = 6 the elements at index 2 and 3 in P will not be swapped. But if d₂ = 3 and d₃ = 1 they will definitely cross one another, and hence, be swapped.

e)Given any vector v obeying conditions a),b),and c), a sequence T exists such that v is its displacement vector. (Since the sum of the entries will be 0, either all entries will be 0, or there will be some negative entries and some non-negative entries, Hence, when going clockwise and starting from a non-negative entry, there will at some point be a non-negative entry immediately followed by a negative entry, and hence by swapping these two elements in P and updating v accordingly we will obtain a new vector that imply a smaller number of swaps. We iterate this procedure until we get a zero displacement vector, at which point the swaps that we performed will form the required sequence T).

f)Let d be some displacement vector. Define I(d) to be the number of swaps implied by d. To improve d means to change it such that I(d) becomes smaller. Assume the maximum entry in d is M = d_i and the minimum is m = d_j. Also assume that M - m > n. Then it is possible to improve d by subtracting n from d_i and adding n to d_j. (This corresponds to changing the sense of travel of i and j).The paper cited above calls this a contracting transformation. Repeatedly improving the displacement vector leads to an optimal solution. I will later post an update to prove this.

Algorithm Description:

This is the algorithm for two linear permutations, with adjacent swaps allowed, as well as swapping the first and last elements. As noted above, the circular permutation problem can be easily reduced to this one.

First we assume without loss of generality that the first permutation is the identity permutation, and let us call the second permutation Q;

The initial displacement vector of Q is the vector V such that, for every i,V_i = Q_i - i; Then, as long as there is a pair of indices (i, j) such that V_i - V_j > n, we increase V_j by n and decrease V_i by n. W**hen this process finishes, we count the number of crossings implied by the new displacement vector.

This is the entire description of the algorithm. It is short and simple to implement.

A naive analysis of the running time would be as follows: the number of contracting transformations is bounded by the number of swaps (O(n²)) and getting the minimum and the maximum at every iteration takes O(n). The process has to be repeated for O(n) rotations of the permutation Q so the total running time is O(n⁴). A better runtime analysis (to be given later) will show the running time to be equal to O(n³). I think that a more sophisticated implementation using a map for getting the min/max and a segment tree or a divide-and-conquer algorithm to compute the number of swaps for the optimal displacement vector would result in a O(n²log(n)) algorithm. More details on this later.

MohammadFatafta

For problem K, are you sure that a is always less than b in the input?

because when I tried to put the assertion: assert(a<b); after I read a & b, I get a runtime error verdict, while when I remove it I get a wrong answer, so clearly this assertion fails, or something is wrong idk :|

I tried reading a & b as both unsigned long long & long double, and I keep getting the same thing...

I don't know, I don't have direct access to the test cases. The ones that have been generated on the polygon system look correct, but I don't think they are the same as the ones used in the codeforces contest, because for instance in the case of problem H, many attempts failed on the second test case, which is only the second test case in the sample input on the copy of the test cases I have.

Well, now I'm sure in the input they have some cases where a>=b, as I modified my code to solve these cases and now it's AC.

I think the one who prepared the contest should remove the line that says a<b from the problem statement.

Thank you for the nice problems.

Oops you're right. Even on the test cases I have on the polygon system, there are test cases with a = 99 and b = 7. Sorry for that.

It's ok :D

That simple constraint took 40 submissions from me though lol.

Removed the incorrect test cases, sorry.

uttom

how can redudecd to problem "A" equation?? please explain it.. Thanks in advance

KhaledKEE

← Rev. 2 →

$\text{[math]}$
They are two trivial cases.
For other ranks, the number can do the same as the one before it (i.e go to ranks less than the one before it) or go to the rank before it and do the same.
$\text{[math]}$
It's easy to see that:
$\text{[math]}$
$\text{[math]}$