Div2
BearSong (250p.)
There are two ways to solve this problem. The first way is to create an array T of size 1000 to count occurrences of each note. For each number x in the given sequence we should do T[x]++. After that, we should iterate over T and count the number of indices with value 1.
There is an alternative O(N2) solution. For each element of the given sequence we can iterate over other elements to check whether some of them is equal to the current one.
BearSlowlySorts (500p.)
Again, there are two ways to solve a problem. The first one is quite boring. One could notice that the answer must be small and we can simulate first few moves in any possible way. Some extra observation is that after sorting the first N-1 we shouldn't sort them again in the next move. So we should either do moves in the order {first, last, first, last, ...} or {last, first, last, first, ...} — there are only two possibilities.
With some cases analysis you can find solve this problem even without sorting. The crucial observation is that we care mostly about the smallest number and the largest one.
- The answer is 0 only if the sequence is already sorted.
- If the first number is the smallest one (thus, we don't have to move it), then the answer is 1.
- If the last number is the largest one, the answer is 1.
- If the first number is unfortunately the largest and the last number is the smallest one, the answer is 3.
- Otherwise, we can sort a sequence in 2 moves.
BearPermutations2 (1000p.)
O(N4) solutions should get AC but I will describe a O(N2) solution. We want to find an answer for all n up to given N.
For fixed n let's iterate over all n possible places to put the smallest number. Let where denote an index of the smallest number. The smallest number divides n numbers into two almost independent groups A and B and the equation |A| + |B| + 1 = n holds (moreover, |A| = where - 1, |B| = n - where). There are 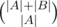 ways to divide numbers into two groups. For fixed division of numbers and for fixed position of the smallest number in A there are (|A| - 1)!·|B|! ways to arrange numbers. Note that it doesn't matter what "position of the smallest number in A" we chose.
ways to divide numbers into two groups. For fixed division of numbers and for fixed position of the smallest number in A there are (|A| - 1)!·|B|! ways to arrange numbers. Note that it doesn't matter what "position of the smallest number in A" we chose.
For nonempty A and B for any arrangement the difference between indices of the smallest numbers in A and in B could be written as a sum of two terms:
- the difference between an index of the smallest number in B and a value where defined before. Note that such a distance is in interval [1, |B|].
- the difference between where and an index of the smallest number in A
Calculating the two terms above separately allows us to calculate everything for A and for B separately. Now, we can sum up 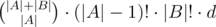 for all
for all  so it's enough to add
so it's enough to add 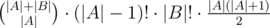 to the result. There is |A| - 1 because the smallest elements is chosen and placed already. More details in my code.
to the result. There is |A| - 1 because the smallest elements is chosen and placed already. More details in my code.
Div1
BearCavalry (300p.)
For each horse let's assume that it is assigned to Bravebeart and let's calculate the number of ways to assign other horses to other warriors.
For each case let's sort all other warriors and all other horses. With two pointers we can find for each warrior what horses he can get (it's limited by the strength of the Bravebeart's unit). We now know the number of ways (let a denote it) to assign a horse to the strongest warrior. He takes one horse and it was one of the horses the next (second strongest) warrior could get. We calculated that the second strongest warrior can take one of b horses but one was taken so he can b - 1 possibilities. The third warrior could take c horses but two are taken so we multiply some variable (result for this case) by c - 2. And so on. For each case we should add a·(b - 1)·(c - 2)·... to the result.
BearPermutations (600p.)
Read the Div2-Hard editorial first. The task there was to sum up scores for the given N.
In O(N4·S2) we could do the following dynamic programming. dp[n][where][S] is the number of n-permutations with the smallest number in position (index) where and the score equal to S. The main line of our program would be:
dp[n1+n2+1][n1+1][S1+S2 + n1+1+where2 - where1] += binom[n1+n2][n1] * dp[n1][where1][S1] * dp[n2][where2][S2]
We can notice that terms S2 and where2 appear only in one dimension of the resulting dp[][][]. The same for S1 and where1. Thus, we can create an array dpLeft[n][sw] to store the sum of dp[n][where][s] that where - s = sw. Similarly, we should create an array dpRight[n][sw]. You can additionally notice that these two arrays are similar and we need only one of them.
BearGirls (1000p.)
Backwards dynamic programming. What is hard to calculate is f(k, r) denoting the expected value of the r-th biggest number among k randomly chosen ones. It turns out to be simple to calculate because f(k, r) = p·f(k + 1, r + 1) + (1 - p)·f(k + 1, r) for 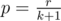 . Don't be misled by words "simple to calculate". It took me literally weeks to solve this problem and I don't say that it is easy to find the formula above.
. Don't be misled by words "simple to calculate". It took me literally weeks to solve this problem and I don't say that it is easy to find the formula above.
Looks like binomial coefficient, right? And this is how we can prove its correctness. When we have k numbers and the r-th biggest one is marked, we can still add other numbers one by one. The new number will be greater with probability 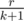 . You can find my code above.
. You can find my code above.
You may wonder why there was some cost given. The problem would be fine without it but well written O(N3) solution could be squeezed to pass then.











A and B were too easy then C was out of 95%'s reach, making this just a speed contest. I didn't enjoy it much.
I wonder if there's some kind of TC specific forum or platform to declare such opinions — it makes no sense to say this on codeforces.
P.S. thanks anyway if you are the contest writer, hopefully this is a constructive input for the future.
P.S. Div 2 here
I think that CF is the best place to write a feedback. I'm sure that all authors of SRMs visit CF (and that they don't often visit a bit dead TC forum). And thanks for your opinion, I will try to make d2-Hard a bit easier the next time
Thanks for writing back!
Concisely; here is what I think would have made this more of a standard TC round: - a little bit harder B - More hack/error prone A and B
Quick stats from the small random sample that is my room: 17 participant opened problems
Stats speak my points out loud, I think. e.g. it's okay (and actually favorable) for 100% of participants to submit solutions for A but a disaster for them all to pass system tests.
I have never solved Div 2 C in contest so I can give no review on that.
Thanks for the lovely problem set again! They were all well-written and clear.
why -1 in (|A| - 1)!·|B|! for div2 1000?
there was some small mistake. I changed it and added some explanation.
What do you mean by 'in one dimension'? I see that where2 appears in term
dp[n2][where2][S2]and in termdp[n1+n2+1][n1+1][S1+S2 + n1+1+where2 - where1].Product of
dp[n1][where1][s1]anddp[n2][where2][s2]must be added todp[A][B][C]where A and B do not contain s2 or where2. Only dimension C depends on values of s2 and where2.So, we can use something similar to prefix sumes. We need an extra array with sum of all
dp[n2][where2][s2]with the same value ofs2+where2.Now we can replace O(N) operations with one operation:
dp[n1+n2+1][n1+1][S1+S2 + n1+1+where2 - where1] += binom[n1+n2][n1] * dpSumLeft[n1][s1-where1] * dpSumRight[n2][s2+where2]--- EDIT ---
In code we want the following line:
dp[n1+n2+1][n1+1][X + Y] += binom[n1+n2][n1] * dpSumLeft[n1][X] * dpSumRight[n2][Y]where X represents the value of s1 - where1 and Y is the value of s2 + where2. Note that in my implementation X is named s1 and Y is named s2.
EDIT2. Thanks for Avitella for finding a mistake/typo.