606A - Магические сферы. Посчитаем, сколько сфер каждого типа недостаёт до цели. Нам надо провести по крайней мере столько преобразований. Посчитаем, сколько сфер каждого типа лишние по сравнению с целью. Каждые две лишние сферы дают нам возможность провести одно преобразование. Поэтому, чтобы понять, сколько преобразований можно сделать из данного вида сфер, надо посмотреть, сколько есть лишних сфер, поделить на 2 и округлить вниз. Сложим все возможности преобразований из каждого вида сфер и все недостачи. Если возможностей преобразований не меньше, чем недостач, ответ на задачу положительный. Иначе – отрицательный.
606B - Испытания роботов. Заведём матрицу, где для каждой клетки будем хранить, в какой момент робот впервые посещает её при прохождении маршрута. Чтобы найти эти величины, пройдём роботом весь маршрут. Каждый раз, когда приходим на клетку, в которой мы ещё не были, сохраняем в соответствующую ячейку матрицы, сколько сейчас сделано действий.
Заведём массив счётчиков, в котором для каждого возможного количества действий будем хранить, сколько вариантов было, когда робот взорвётся после такого количества действий.
Теперь переберём все возможные клетки, где может находиться мина. Для каждой клетки, если она не посещена роботом, добавим одно прохождение из N действий, где N – длина маршрута. А если посещена, добавим одно прохождение из стольки действий, сколько написано в этой клетке (когда она была посещена). Ведь если мина в этой клетке, робот взорвётся сразу после первого её посещения. Массив счётчиков теперь – ответ на задачу.
605A - Сортировка вагонов. Предположим, мы убрали из массива те элементы, что будем переставлять. Что останется? Останется последовательность подряд идущих чисел: a, a+1, …, b. Длина такой последовательности должна быть максимальна, чтобы минимизировать число элементов, которые надо переставлять.
Рассмотрим массив pos, где pos[p[i]] = i. Посмотрим на его подотрезок pos[a], pos[a+1], …, pos[b]. Эта последовательность должна возрастать, а ее длина, как уже сказали выше, должна быть наибольшей. Таким образом, надо выделить наибольший подотрезок в массиве pos, где значения pos[a], pos[a+1], …, pos[b] идут в возрастающем порядке.
605B - Неуспевающий студент. Упорядочим рёбра по возрастанию длины, а при равенстве будем ставить раньше те рёбра, которые просят включить в MST. Начнем добавлять их в граф в этом порядке. Если текущее ребро просят включить в MST, соединим этим ребром 1-ю вершину с наименьшей изолированной пока ещё вершиной. Если текущее ребро просят НЕ включать в MST, соединим этим ребром две какие-то связанные ранее вершины, между которыми ещё нет ребра. Это удобно делать, поддерживая два указателя на вершины (назовём их from и to). Изначально from=2, to=3. Когда нам нужно соединить две связанные вершины, мы добавляем ребро (from, to) и увеличиваем from на 1. Если при этом from оказался равен to, мы делаем вывод, что мы уже добавили все возможные рёбра в вершину to, увеличиваем to на 1, а from устанавливаем на 2. Это значит, что с этого момента не-MST-шные рёбра мы будем проводить из to во все вершины начиная со второй. Если окажется, что to указывает на изолированную пока ещё вершину, мы можем сделать вывод, что в графе в настоящий момент нет места для не-MST-шного ребра и ответ Impossible. В итоге мы будем добавлять MST-шные ребра как (1,2), ..., (1,n), а не-MST-шные в порядке (2,3), (2,4), (3,4), (2,5), (3,5), (4,5), …
605C - Мечты фрилансера. Разрешим не получать денег или опыта за некоторые проекты. Добавление такой возможности не изменит ответ. Пусть герой потратил T времени на выполнение мечты. На каждый проект он потратил часть этого времени (возможно, нулевую). Тогда средняя скорость зарабатывания денег и опыта героем была линейной комбинацией скоростей зарабатывания на всех эти проектах, с весами равными долям времени, затрачиваемого на каждый из проектов.
Построим множество точек P на плоскости (x,y) таких, что мы можем получать x денег и y опыта в единицу времени. Расположим точки (a[i], b[i]) на плоскости. Добавим также точки (max(a[i]), 0) и (0, max(b[i])). Все эти точки точно принадлежат P. Найдём их выпуклую оболочку. После этого любая точка внутри или на границе выпуклой оболочки будет соответствовать использованию какой-то линейной комбинации проектов.
Теперь осталось выбрать точку, которую нужно использовать герою в качестве средней скорости зарабатывания денег и опыта за всё время реализации мечты. Она должна быть в пределах выпуклой оболочки. Мечта реализована, если мы придём в точку (A,B). Задача позволяет нам прийти правее или выше, но это сделать не проще чем прийти в саму точку (A,B). Поэтому направим в эту точку луч из (0,0) и найдём самый поздний момент, когда этот луч проходил по нашей выпуклой оболочке. Это будет соответствовать самой большой скорости набирания ресурсов, какую мы можем себе позволить в направлении точки (A,B). Координаты этой точки — это скорости, с которыми будут набираться ресурсы.
Чтобы найти саму точку, надо пересечь луч с выпуклой оболочкой.
605D - Настольная игра. Рассмотрим n векторов с началами в точках (a[i], b[i]) и концах в точках (c[i] и d[i]). Запустим поиск в ширину. На каждом его этапе нам необходимо выполнять такую операцию: получить множество векторов, у которых начало принадлежит прямоугольнику 0 <= x <= c[i], 0 <= y <= d[i], и больше не рассматривать эти векторы никогда. Это делается так. Сожмём координаты х. Для каждого x будем хранить список векторов, чья первая координата равна x. Заведем дерево отрезков, у которого индекс будет равен первой координате, а значение — второй координате. Дерево отрезков должно уметь находить индекс минимума на отрезке и проставлять значение в точке. Теперь пусть нам надо найти все векторы, у которых первая координата от 0 до x, а вторая от 0 до y. Найдем индекс минимума в дереве на отрезке [0, x]. Он укажет на вектор (x,y), у которого x — это тот самый индекс минимума, а y — значение минимума. Удалим его из списка векторов (добавив также в очередь поиска в ширину) и присвоим в дерево отрезков на этот индекс вторую координату следующего вектора с первой координатой x. Делаем так, пока минимум на отрезке все еще меньше y. Таким образом, на каждом шаге мы будем получать список еще не посещенных векторов в левом нижнем прямоугольнике, и каждый вектор будет получен ровно 1 раз, после чего он будет удален из структур данных.
605E - Межгалактические путешествия. Вершина тем более хорошая, чем меньше матожидание числа ходов из нее, чтобы добраться до финиша. В целом стратегия такова: если можно пойти в вершину, которая является более хорошей, чем текущая, то надо идти в нее, иначе оставаться на месте. Подобно алгоритму Дейкстры, будем хранить оценки ответа для каждой вершины, и фиксировать эти оценки как окончательный ответ в порядке от лучших вершин к худшим. На первом шаге мы зафиксируем вершину N (ответ для неё – 0). На втором шаге – вершину, из которой проще всего попасть в N. На третьем шаге – вершину, из которой проще всего закончить, переходя в вершины, определенные на первом и втором шагах. И так далее. На каждом шаге мы находим такую вершину, которая дает наилучшее матожидание числа ходов, если переходить из нее в вершины лучше нее, и фиксируем это матожидание – оно уже не может улучшиться.
Для каждой ещё незафиксированной вершины мы можем найти оценку, каково матожидание времени пути до финиша из неё. В этой оценке мы учитываем знание о вершинах, для которых ответ уже известен. Мы перебираем вершины в порядке неулучшения ответа для них, поэтому ответ для оцениваемой вершины не лучше, чем для уже перебранных. Посмотрим, как выглядит выражение для матожидания времени достижения финиша из вершины х, если пользоваться тактикой “идти в лучшую из i доступных вершин, для которых ответ уже известен, или стоять на месте”:
m(x) = p(x, v[0]) * ans(v[0]) + (1 — p(x, v[0]) * p(x, v[1]) * ans(v[1]) + (1 — p(x, v[0]) * (1 — p(x, v[1]) * p(x, v[2]) * ans(v[2]) + … + (1 — p(x, v[0]) * (1 — p(x, v[1]) * … * (1 — p(x, v[i-1]) * m(x) + 1
Здесь m(x) – оценка для вершины х, p(a,b) – вероятность существования ребра (a,b), а ans(v) – известный ответ для вершины v. Заметим, что m(x) выражается через себя, т.к. есть вероятность, что придётся остаться на месте.
Будем помнить оценочное выражение для каждой вершины в виде m(x) = A[x] * m(x) + B[x].
Для каждой вершины будем хранить A[x] и B[x]. Это будет значить, что с какими-то вероятностями удастся сдвинуться в более хорошую вершину, и эта возможность даёт вклад в матожидание B[x], а с какой-то вероятностью придётся оставаться на месте, и эта вероятность A[x] (она совпадает с коэффициентом перед m(x) в формуле).
Итак, на каждом шаге мы выбираем незафиксированную ещё вершину v с наименьшей оценкой, фиксируем её и производим релаксацию из неё, обновляя оценки для остальных вершин. Когда обновляется оценка для вершины x, мы изменяем её A[x] и B[x]. A[x] уменьшится на величину A[x] * p(x,v), т.к. вероятность, что придётся остаться на месте, подразумевает, что в вершину v тоже пойти не удалось. B[x] увеличится на величину A[x] * p(x,v) * ans(v), здесь A[x] – вероятность, что не удастся воспользоваться вершиной, более хорошей, чем v, A[x] * p(x,v) – вероятность, что при этом удастся воспользоваться вершиной v, а ans(v) – известный ответ, который мы только что зафиксировали для вершины v.
Чтобы посчитать, какова всё-таки оценка ответа для вершины, мы можем взять формулу m(x) = A[x] * m(x) + B[x] и выразить m(x). Именно m(x) нужно хранить в очереди с приоритетами для нашего аналога Дейкстры, и именно m(x) фиксируется как окончательный ответ для вершины х, когда она объявляется вершиной с наименьшей оценкой в начале шага.










Автокомментарий: текст был обновлен пользователем craus (предыдущая версия, новая версия, сравнить).
My solution to C: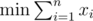 subject to
subject to 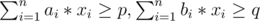 . The dual of this problem is max p * y1 + q * y2 subject to ai * y1 + bi * y2 ≤ 1. It's convex, so we can use a simple ternary search.
. The dual of this problem is max p * y1 + q * y2 subject to ai * y1 + bi * y2 ≤ 1. It's convex, so we can use a simple ternary search.
wow it's Too Simple!
TooSimple*
your joke is too outdated now :D
I actually find it Too Difficult now :)
Could you explain how do you get dual of the problem, please?
http://web.mit.edu/15.053/www/AMP-Chapter-04.pdf
You can check this lecture. Duality in linear programming is very important in combinatorial optimization problems like graph matching and many approximation algorithms.
Although simplex works in time O(C(n + m, m)) it passed system tests.
Not Too Simple, it is Too Simplex
Not TooSimple but truly subtle!!
I'm not able to understand why the function is convex. Can someone please explain?
Can anyone please tell me the complexity of Simplex Method to solve Linear Programming problems? I used that method to solve C, but I do not know its complexity.
Why does the second test case of Div. 2 problem D (Div. 1 problem B) return -1?
IN:
3 3
1 0
2 1
3 1
OUT: -1
Thanks
The graph consists of three vertices and three edges — there is an edge between each pair of vertices. For the MST we need to pick two of the edges so that their sum is minimum — therefore we pick the edges with weights 1 and 2. However, Vladislav didn't include the edge with weight 1 in his MST.
But why this test case does not return -1? A edge with weight 3 is not chosen, but a one with 4 is. Shouldn't we choose the one with 3?
IN:
4 4
2 1
3 0
3 1
4 1
OUT:
1 2
2 3
1 3
1 4
If we look at the graph that the output creates, we can see that the only way that we can reach vertex 4 is by using the edge between vertices 1 and 4. There's no spanning tree on the graph that does not include the vertex with weight 4.
Isn't the following graph valid as an output for this example (supposing we take vertex with weight 3 instead the one with 4)?
1 2
2 3
3 4
1 3
Yes.
The task was to reconstruct one of the graphs that match Vladislav's description. There are multiple different answers for sample 1. However for sample 2 no graph matches the description.
This is due to the Minimum-Cost Edge property of a MST.
If the edge of a graph with the minimum cost e is unique, then this edge is included in any MST.
Proof: if e was not included in the MST, removing any of the (larger cost) edges in the cycle formed after adding e to the MST, would yield a spanning tree of smaller weight.
In the given graph, 1 is the minimum cost edge but it is not included in the MST, hence no graph is possible.
Source: Wikipedia
But why this test case does not return -1? A edge with weight 3 is not chosen, but a one with 4 is. Shouldn't we choose the one with 3?
IN:
4 4
2 1
3 0
3 1
4 1
OUT:
1 2
2 3
1 3
1 4
Тут меня спрашивают про задачу С див 1, почему линейная комбинация лежит в выпуклой оболочке. Ну, мне самому тоже интересно стало, почему, и вправду. Спросил у старших товарищей. Говорят, по определению о_О
Ну там я имел в виду, что линейная комбинация с коэффициентами, дающими в сумме 1. Причем ещё чтоб все коэффициенты не отрицательные были. Оказывается, это называется выпуклая комбинация.
I really liked Div1 B, very original and different problem. The ones where you reconstruct a graph from some information are always interesting.
During the contest I (mis)read Div2A as requiring that I turn (a,b,c) into exactly (x,y,z). Out of curiosity does anybody know how to solve that problem?
Oh facepalm I read it as this too. No wonder I couldn't solve it during the contest :/
Because of this, I thought about it for a long time near the beginning--found out that you could get (-1 -1 -1) in 3 steps, (-1 -1 0) and permutations in 2 steps. But you can't get (-1 0 0) in 1 step, and therefore can't get (x-1 y z) within (-x — y — z + 1) steps. Couldn't figure out much more, so moved on to other problems.
Я правильно понимаю, что в С размер выпуклой оболочки худшего теста несколько меньше n и есть величина порядка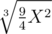 , где X = 106 ограничение на каждую координату?
, где X = 106 ограничение на каждую координату?
The solution for 606A Magic Spheres presented here is trivial, but is it really correct?
I spent almost an hour during the contest figuring out how to balance the amount of rocks in each pile so that the final distribution is exactly equal to the final requirements.
For example, what if a=b=c=1 and x=y=z=0??? In that case it would be impossible to reach this final distribution, even though your simplistic solution gives a positive answer.
Can someone explain why the author's solution is NOT wrong? Or is the problem formulation incorrect?
"To make a spell that has never been seen before, he needs at least x blue, y violet and z orange spheres."
Damn it...
Charlie Foxtrot.
I added edges in a different manner. all the mst edges were added as (1,2) , (2,3) , (3,4).. and then non — mst edges were added as (1 3) ( 1 4 ) ... (1,n) (2 4)...(2,n)....... Why is this wrong?
I did the same thing. Can't figure why this is wrong
Say, by your method the edges added were of weight 2 between 1,2 and 2,3 and weight 3 between 1,3. Let all other edges be in the MST.
This does not give the correct spanning tree for the graph.
I’m not sure I follow. What’s the input and what’s the graph?
Making the MST edges (1, 2), (2, 3), (3, 4), (4, 5), ... isn’t wrong, and my solution doing that got accepted.
Make sure you increment the larger index only when you run out of the smaller index’s range, not the other way round: (1, 3), (1, 4), (2, 4), (1, 5), (2, 5), (3, 5), (1, 6), ... If you try to increment the larger index first, you’ll find that for some k you’ll try to add edge (1, k) before you add edge (k - 1, k), so you’ll skip it and go back to (2, 4), and eventually you’ll run out of space to add new edges and incorrectly conclude that the corresponding graph can’t exist.
Also make sure to look at edges that are within the MST before edges that are outside it but have the same cost.
В задаче Е зашло такое вот итеративное решение 14736802. Это норма? Оно правильное само по себе? Не ломается?) Я просто эту штуку чисто как прием знаю и юзаю, но доказывать/обосновывать, кроме как "на каждой итерации ответ получается не хуже, чем предыдущий", не умею.
Суть решения — на каждой итерации для каждой вершины пытаться срелаксировать ответ через возможность походить в те другие вершины, в которых ответ меньше, чем в текущей.
Странно, у меня такое не зашло, кажется легко придумать тест против любого количества итерауций меньшего n-3.
Если в вашей первой посылке 14730424 заменить в двух местах
100*nна100*(n-1), то будет АС =)Фигня какая-то =) Думал так сделать, но понял каким тестом валится и забил(
D is also could be solved with divide-and-conquer. The first step is to reduce problem to 0-1 bfs (we can always decrease our skills for free and can cast one spell to change the skills from (a,b) to (c,d)). If we add all edges there will be O(n2) 0-edges, but it's possible to add additional vertices in such way that we will only need
additional vertices in such way that we will only need  0-edges and path in our new graph will correspond to path in old graph with same length.
0-edges and path in our new graph will correspond to path in old graph with same length.
So, how to add new vertices in that way? Let's separate all initial vertices into two halves such that all vertices in the first half is on the left from vertices in the second path. There will be vertical line divides all vertices in that way. Denote it's x-coordinate as x0. We have to add vertices with coordinates (x0, y0), (x0, y1), ..., (x0, yk) where y0, ..., yk are all y-coordinates of the whole set of vertices. (y0 < y1 < ... < yk). For the vertex (x, y) such that x ≤ x0 we should add edge from (x0, y) and if x ≥ x0 it would be edge from (x, y) to (x0, y). Also we should add edges from (x0, yi) to (x0, yi - 1) for every possible i.
That's it, then we should find shortest path in that 0-1 graph.
The simple search maximum increasing subsequence in problem C. And answer in n-maxsub
14742819
Can someone plz explain me Div2 C in easy language and why we are making pos array as mentioned in the editorial.
PLZZZZZZZ.
We are looking for the largest possible set of numbers that we will not touch during the sorting (longest increasing subsequence), every other element is going to be moved either to the front or to the back.
If two numbers, lets say 4 and 5, are part of such set, 5 must occur after 4. The fastest way to check this is if we have stored the location of 4 and 5 in pos, so that we can simply check whether ( pos[4] < pos[5] ) is true.
By iterating through the pos array we can easily find the longest segment where the equation holds for each pair of consecutive elements.
Can you please explain how we are finding Longest Increasing Subsequence in Linear time?
This is a special case since the N elements are numbered from 1 to N. For example, sorting such an array requires a linear amount of work since we can simply assign every element to the position indicated by their number.
In this task, we can find the longest increasing subsequence by checking the cars from 1 to N in a single loop. The standard LIS algorithm involves binary searching, but our pos array replaces the O(logN) searching with O(1) array lookups. Such an array could not be constructed if the element values were not bounded by N.
It is not longest increasing subsequence. It is longest increasing subsequence WHERE EACH PAIR OF ADJACENT ELEMENTS DIFFER BY 1.
I am confused :/ Is it longest increasing subsegment (as written in editorial) or longest increasing subsequence? Or it is longest increasing subsequence WHERE EACH PAIR OF ADJACENT ELEMENTS DIFFER BY 1 .. ?!
It depends on the array (input / pos)
couldn't get till now :( maybe I should try something else and then try this again..
actually we have to find "**lics**"-> longest increasing consecutive subsequence
i dont get it in test 21:
7
1 3 5 7 2 4 6
the lics(longest increasing consecutive subsequence):
will be 1 3 5 7
but the answer is 5 what am i doing wrong here ?
Got it thankyou
In Div2D,shouldn't tie breaker be the other way round? Placing the edges included in the MST earlier?
Yes, I think so. I got accepted with the tie breaker you said, and placing earlier edges that we were asked not to include in the MST would fail (using the algorithm described) in cases like this:
3 3 1 0 1 1 1 1
I think x)
Thank you. Sure the tie breaker should place MST-edges first. It was mistake on translation. Fixed.
In div1 C why do we need to add points (max(a[i]), 0) and (0, max(b[i])) to our set of points? If I'm not wrong, is this done to ensure that our ray definitely intersect with our convex hull?
yes
I don't know but seems I can't understand test 8 in problem Div2A: 2 2 1 1 1 2 Jury's Answer is No. But simply we transform one blue and one violet into one orange and we get 1 1 2 Which is required, so why is the answer no? Can anyone explain?
Ah I got it, we most transform two of the same color, now I get it
Can anyone explain the solution to Div-1 C given in the editorial a bit more? Why is the given problem solvable using Convex Hull and the intuition behind it?
Think of the distinct projects as vectors pi = (ai, bi). On time t you can reach any of the points t·pi, but you can also reach any convex combination of them. The points that can be obtained as a convex combination of a certain set of points is the convex hull of that set.
If you take into account that, whenever is possible to reach (x, y) you can also reach any (x', y') such that 0 ≤ x' ≤ x and 0 ≤ y' ≤ y (that is the rectangle with corners in (0, 0) and (x, y)). You also need to add (0, 0), (0, maxy) and (maxx, 0) to the set {t·pi}1 ≤ i ≤ n. The set of points reachable on time t will be those contained in the convex hull. You can do binary search or some vector calculations to find out what is the minimal t such that the target point lies inside it.
Hope it's clear.
Why does the editorial not mention anything regarding binary search? is it using a different logic?
Div 1 D.
Very Nice question.. I never did a bfs using a RMQ tree before. Cool!!
Thanks for the question
For Div1.E:
"The overall strategy is: if it is possible to move to vertex better than current, you should move to it, otherwise stay in place."
Can anybody prove it?
For div2 C, some people did something seemingly very simple, but I have no idea why something like the following works:
Div1 A / Div2 C anyone tried using binary search ?? I have an idea, but I ain't getting how to go forward. Let us say the minimum number of moves required to sort the whole array is M. clearly, for any number of moves less than M,we can't sort. Now, for any number of moves greater than M, we can always sort the whole array ( keep removing element from the end and place it on the end ). Thus, I think it is valid to say that the number of moves M can be binary searched. Now, I can't understand how to move forward, i.e. given number of moves, how to check if sorting can be done ? Also, I would like to know if my method is correct or not ?
Maybe you can check all subarrays (after sorting) Of size N-M (if you will move M elements then N-M will be left) And check if it's possible to find any one subsequence whose size is >=N-M and they form a subarray of sorted array
Now think about how to do that... I haven't thought about it but maybe this should work...
Hmmm......I understood what you are saying,but does that mean "what ever I do, I must find the longest increasing subsequnce " ? Because even after using binary search, you are actually finding the longest increasing subsequence (in the step when optimal value of M is found). So, won't that make binary searching useless ( as we could directly find the answer by finding longest increasing subsequnce ) ?
Nope maybe you can use sliding window on vector pair ( value,index) and check if there exist a susequence in given array forming subarray in sorted array
For problem B lazy student first of all, let's consider what we do in order to construct an MST.
1)Sorting all the edges in ascending order of their weight. 2)Pick the smallest edge(not selected till now)check whether it forms a cycle or not. If it doesn't form a cycle include it in the spanning tree else discard it. 3)Repeat step 2 until we have got V-1 edges in the spanning tree. 4)The spanning tree that we have now is the MST.
This same thing is written in the editorial first of all sort the edges in ascending order, then if the current edge needs to be included in the MST include it else if the edge is supposed to be discarded from the MST then it must form a cycle in the spanning tree constructed till now otherwise it would contradict the condition of getting discarded which is an edge is discarded if and only if it forms a cycle in the spanning tree constructed till now. If the edge to be discarded doesn't form a cycle then a graph having a corresponding spanning tree given would not exist. my submission=>https://mirror.codeforces.com/problemset/submission/605/94260114