sophisticated1's blog

Another Combinatorics Problem (Codechef Long Problem)
By sophisticated1, history, 9 years ago, In English

How to solve this problem from recent Codechef Long Challenge??

https://www.codechef.com/DEC15/problems/MGCHPERM/

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by sophisticated1 (previous revision, new revision, compare).

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Hi! i guess the answer is polynomial of k-th degree. So you could just use Lagrange Interpolation. Again it is only guess.

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +22 Vote: I do not like it

Ok, here's how I solved it:

First of all notice that given a set of lengths s, they represent a convex polygon if (assuming s is sorted, so s|s| is the largest element). A kind of "generalized triangle inequality". Rearranging yields: .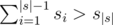

So the problem is: Given the set {1, 2, 3, ... n}, how many k element subsets obey our equation? Constructing an dp solution based on that should be pretty straightforward. That gives 30 points already.

In order to optimise further, we need some combinatorics: How about counting the number of subsets that do not work? Then the answer is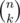 — (this number). Turns out this is easier to compute (..at least for me ^^). So .

Let's solve for equal first. That is, given the highest element, in how many ways can we select k - 1 smaller numbers, such that their sum is equal to this highest element. That can be computed once again using dp in . To handle "smaller equal" and not just "equal", we can use a "kind of prefix sum" (consult my submissions for details). That results in 60 points.

To gain full score, we have to transform the recurrence into a matrix (my matrix has dimensions ((k - 1)2 + 2) × ((k - 1)2 + 2) — basically keeping track of the previous f(n, k) values, 1 as well as the answer). Using matrix exponentiation we can compute the result in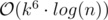 per test case. That's still not fast enough.

To optimise, notice that there are just 7 - 3 + 1 = 5 different matrices we're taking powers of. So I just precomputed the powers of two for these matrices (taking per matrix). For each query you then just multiply your result vector with the corresponding powers of two. That reduces the time per testcase to 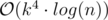and gives full score.

You can check my submissions here — they're basically representing the though process I've described above.

I hope that gives you an idea. The details are "left as an exercise for the reader" :P. Nah, just kidding — I can elaborate if you don't understand parts of it. But try it yourself first, it's really not that hard + a lot of fun as well :)

UPD: The editorial has been published: here

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Ok, it doesn't seem to be a polynomial:)

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Note, that if you have a recurrence of degree k, you can calculate nth element in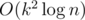 time by exponentiating polynomials modulo polynomial, no precalculations required. Also if you know that your recurrence is of length k, and can easily calculate the first 2k values, then using Berlekamp–Massey algorithm you can immediately get the recurrence in O(k2).

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      That certainly sounds interesting!

      Could you describe some more details? I'm not really getting the idea yet :)

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        I'll show an example, hope it will be clear how to use it in general case.

        Suppose we want to calculate a recurrence an = 2an - 1 - 5an - 2, a0 = 1, a1 = 2:

        1, 2,  - 1,  - 12,  - 19, 22, 139, 168,  - 359,  - 1558,  - 1321, ...

        Move everything to the left side:

        an - 2an - 1 + 5an - 2 = 0.

        Take the left side and replace $a_n$ with xn, and remove the common power of x:

        x2 - 2x + 5.

        Now to calculate 10th element of the sequence, calculate

        and multiply the constant term with $a_0$, the next coefficient with a1, etc:

        1795 * 1 - 1558 * 2 =  - 1321 = a10.

        Multiplication modulo polynomial takes $O(k^2)$ time, so exponentiation takes .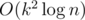

        → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      I can see that polynomial exponentiation can be used to calculate binomial coefficients C(n, k). The multiplication polynomial is 1 + x. So it is indeed complexity instead of when we used matrices exponentiation. However I didn't understand how the polynomial trick can be applied to the problem being discussed.

      Here is an excel table I've created where each F(n, k) is a number of sets that do not work, the value that should be subtracted from C(n, k) in order to receive the answer. I solved the problem using matrices exponentiation with degree 23.

      Is it possible to get a recurrence polynomial from this table?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        Yes, using Berlekamp–Massey algorithm on the last column will give its recurrence relation (though I think you should find partial sums first).

        BTW, in this problem the recurrence polynomial is equal to

        → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Please explain the portion : "generation of matrix from recurrence relation " ??

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it +3 Vote: I do not like it

      Our 60 points recurrence looks something like that (omitting modulo and memorisation):

      int f(int n, int k)
{
	if (n<0)
		return 0;
	if (k==0)
		return 1;
	return f(n-k,k)+f(n,k-1);
}

      We want (the thing, because my recurrence allows xi ≥ 0, so I'm just assuring that xi > 0). In other words: 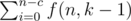, with .

      To calculate something like that using matrix exponentiation, we're basically trying to transform some vector vn into vn + 1, by multiplying vn with some matrix A. vn needs to contain all information to calculate vn + 1.

      I used the following vector:

      The 1 is representing f(n, 0) and sum is the sum of f(n, k - 1) values. Now we need a matrix A, to transform vn into vn + 1. The vector has (k - 1)2 + 2 elements, so we need a matrix of this size as well.

      Here's how my transformation matrix looks like for k = 3:

      It's just the recurrence from above, represented using linear equations.

      So what we want is An - c - k. Multiply that with a vector of "base cases" (e.g. initial values for n = {k - 2, k - 3, ...0 }). Those can be computed using our dp from above in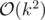 . Once you did that, sum represent the number of "bad" subsets.

      → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by sophisticated1 (previous revision, new revision, compare).

→ Reply