Это решение этой задачи было придумано однажды ночью при разработке совершенно другого контеста :)
Пусть 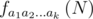 - ответ задачи.
- ответ задачи.
Тогда верен факт (например, можно доказать его из формулы включений-исключений)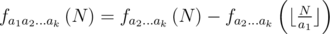
Простой расчет по этой формуле занимает много времени. Можно заметить или знать, что на самом деле аргумент функции достаточно быстро становится маленьким числом, особенно если начальный набор чисел упорядочить по убыванию. Решение с сохранением для маленьких значений аргумента (при должной оптимизации) давало время порядка 1с на худшем тесте и являлось, видимо, неизбежным.
Понятно, что такое решение у меня было, и очень хотелось увеличить ограничение по N раз в 20, чтобы его отсечь, однако не хотелось делать участникам, пишущим на Java, совсем-совсем плохо.
Представим, что мы честно, на листочке, хотим провести расчет по вышеуказанной формуле, например: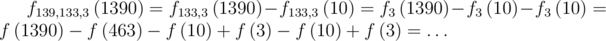
Стоп! Так считала наша программа, а не мы. Мы считали вот так: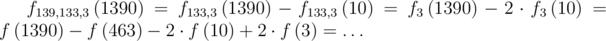
Это толкает нас к следующей идее: будем представлять наше состояние на шаге j двумя массивами Xj и Yj, имея ввиду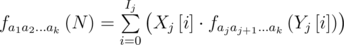
Причем на последнем шаге j = k будем иметь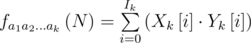
А переход от шага j к шагу j + 1 выполняется по самой первой формуле с последующим слиянием отсчетов с одинаковым Y (массивы в любой момент поддерживаются сортированными, фактически производится слияние прошлого с обновлением и т.д.)
Сложность этого решения, будет, очевидно, 
Утверждение.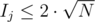
Доказательство.
Любое число, попадающее в массив Y, имеет вид 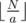 для некоторого натурального a. Заметим, что
для некоторого натурального a. Заметим, что 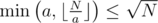
А число вида 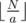 задается однозначно либо
задается однозначно либо 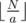 (самим собой), либо a, из чего очевидным образом следует доказываемое утверждение.
(самим собой), либо a, из чего очевидным образом следует доказываемое утверждение.
Таким образом, сложность этого решения 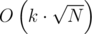
Казалось бы, много (операции деления, все же), но при сортировке по убыванию входных данных наша оценка существенно завышена для первых итераций.
Решение, написанное с оптимизацией хранения для маленьких отсчетов Y (можно посмотреть мои посылки) на сервере CF выполняется порядка 300мс на худшем тесте и укладывается в 2 секунды для N = 1015, k = 100 (т.е. решает задачу при ограничении на N два порядка больше)
Вопросы, предложения, пожелания?
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
21:41:28
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
21:41:28
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 19:53:32 (g1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Объясните, пожалуйста, откуда берется формула. Как ее доказать из формулы включений-исключений?
Выпишем полностью формулу включений-исключений (много букв). Воспользуемся фактом, что
разгруппируем слагаемые, содержащие a1 и не содержащие a1 и применим формулу включений-исключений в обратную сторону.