608A - Сайтама громит гостиницу

Author: ed1d1a8d

Code: https://ideone.com/HiZd9g

The minimum amount of time required is the maximum value of t_i + f_i and s, where t_i and f_i are the time and the floor of the passenger respectively.

The initial observation that should be made for this problem is that only the latest passenger on each floor matters. So, we can ignore all passengers that aren't the latest passenger on each floor.

Now, assume there is only a passenger on floor s. Call this passenger a. The time taken for this passenger is clearly t_a + f_a (the time taken to wait for the passenger summed to the time taken for the elevator to reach the bottom).

Now, add in one passenger on a floor lower than s. Call this new passenger b. There are 2 possibilities for this passenger. Either the elevator reaches the passenger's floor after the passenger's time of arrival or the elevator reaches the passenger's floor before the passenger's time of arrival. For the first case, no time is added to the solution, and the solution remains t_a + f_a. For the second case, the passenger on floor s doesn't matter, and the time taken is t_b + f_b for the new passenger.

The only thing left is to determine whether the elevator reaches the new passenger before t_i of the new passenger. It does so if t_a + (f_a - f_b) > t_b. Clearly this is equivalent to whether t_a + f_a > t_b + f_b. Thus, the solution is max of max(t_a + f_a, t_b + f_b).

A similar line of reasoning can be applied to the rest of the passengers. Thus, the solution is the maximum value of t_i + f_i and s.

608B - Сумма расстояний Хэмминга

Author: ed1d1a8d

Code: https://ideone.com/nmGbRe

We are trying to find 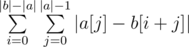. Swapping the sums, we see that this is equivalent to .

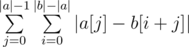Summing up the answer in the naive fashion will give an O(n²) solution. However, notice that we can actually find 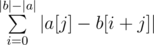without going through each individual character. Rather, all we need is a frequency count of different characters. To obtain this frequency count, we can simply build prefix count arrays of all characters on b. Let's call this prefix count array F, where F[x][c] gives the number of occurrences of the character c in the prefix [0, x) of b. We can then write 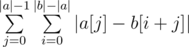. as 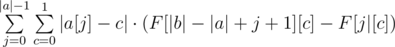. This gives us a linear solution.

Time Complexity — O(|a| + |b|), Memory Complexity — O(|b|)

607A - Цепная реакция

Author: Chilli

Code: https://ideone.com/xOrFhv

It turns out that it is actually easier to compute the complement of the problem — the maximum number of objects not destroyed. We can subtract this from the total number of objects to obtain our final answer.

We can solve this problem using dynamic programming. Let dp[x] be the maximum number of objects not destroyed in the range [0, x] given that position x is unaffected by an explosion. We can compute dp[x] using the following recurrence:

Now, if we can place an object to the right of all objects with any power level, we can destroy some suffix of the (sorted list of) objects. The answer is thus the maximum number of destroyed objects objects given that we destroy some suffix of the objects first. This can be easily evaluated as

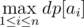
Since this is the complement of our answer, our final answer is actually

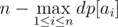
Time Complexity — O(max(a_i)), Memory Complexity — O(max(a_i))

607B - Zuma

Author: Amor727

Code: https://ideone.com/Aw1bSs

We use dp on contiguous ranges to calculate the answer. Let D[i][j] denote the number of seconds it takes to collapse some range [i, j]. Let us work out a transition for this definition. Consider the left-most gemstone. This gemstone will either be destroyed individually or as part of a non-singular range. In the first case, we destroy the left-most gemstone and reduce to the subproblem [i + 1, j]. In the second case, notice that the left-most gemstone will match up with some gemstone to its right. We can iterate through every gemstone with the same color as the left-most (let k be the index of this matching gemstone) and reduce to two subproblems [i + 1, k - 1] and [k + 1, j]. We can reduce to the subproblem [i + 1, k - 1] because we can just remove gemstones i and k with the last removal of [i + 1, k - 1]. We must also make a special case for when the first two elements in a range are equal and consider the subproblem [i + 2, j].

Here is a formalization of the dp:

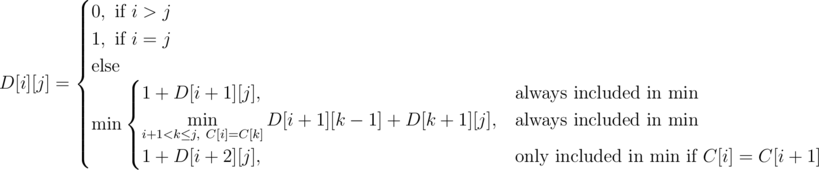
http://mirror.codeforces.com/blog/entry/22256?#comment-268876Why is this dp correct? Notice that the recursive version of our dp will come across the optimal solution in its search. Moreover, every path in the recursive search tree corresponds to some valid sequence of deletions. Since our dp only searches across valid deletions and will at some point come across the optimal sequence of deletions, the answer it produces will be optimal.

Time Complexity — O(n³), Space Complexity — O(n²)

607C - Камушки

Author: ed1d1a8d

Code: https://ideone.com/giyUNE

Define the reverse of a sequence as the sequence of moves needed to negate the movement. For example, EEE and WWW are reverses, and WWSSSEE and WWNNNEE are reverses. I claim is impossible to get both balls to the end if and only if some suffix of the first sequence is the reverse of a suffix of the second sequence.

Let us prove the forward case first, that if two suffixes are reverses, then it is impossible to get both balls to the end. Consider a sequence and its reverse, and note that they share the same geometric structure, except that the direction of travel is opposite. Now imagine laying the two grid paths over each other so that their reverse suffixes are laying on top of each other. It becomes apparent that in order to move both balls to their ends, they must cross over at some point within the confines of the suffix. However, this is impossible under the movement rules, as in order for this to happen, the two balls need to move in different directions at a single point in time, which is not allowed.

Now let us prove the backwards case: that if no suffixes are reverses, then it is possible for both balls to reach the end. There is a simple algorithm that achieves this goal, which is to move the first ball to its end, then move the second ball to its end, then move the first ball to its end, and so on. Let's denote each of these "move the x ball to its end" one step in the algorithm. After every step, the combined distance of both balls from the start is strictly increasing. Without loss of generality, consider a step where you move the first ball to the end, this increases the distance of the first ball by some value k. However, the second ball can move back at most k - 1 steps (only its a reverse sequence can move back k steps), so the minimum change in distance is  + 1. Hence, at some point the combined distance will increase to 2(n - 1) and both balls will be at the end.

In order to check if suffixes are reverses of each other, we can take reverse the first sequence, and see if one of its prefixes matches a suffix of the second sequence. This can be done using string hashing or KMP in linear time.

Time Complexity — O(n), Memory Complexity — O(n)

607D - Могучее Дерево

Author: ed1d1a8d

Code: https://ideone.com/pObeIV

Let's solve a restricted version of the problem where all queries are about the root. First however, let us define some notation. In this editorial, we will use d(x) to denote the number of children of vertex x. If there is an update involved, d(x) refers to the value prior to the update.

To deal these queries, notice that each vertex within the tree has some contribution c_i to the root power. This contribution is an integer multiple m_i of each vertex's value v_i, such that c_i = m_i·v_i If we sum the contributions of every vertex, we get the power of the root.

To deal with updates, notice that adding a vertex u to a leaf p scales the multiplier of every vertex in p's subtree by a factor of 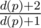. As for the contribution of u, notice that m_u = m_p.

Now, in order to handle both queries and updates efficiently, we need a fast way to sum all contributions, a way to scale contributions in a subtree, and a way to add new vertices. This sounds like a job for ... a segment tree!

We all know segment trees hate insertions, so instead of inserting new vertices, we pre-build the tree with initial values 0, updating values instead of inserting new vertices. In order to efficiently support subtree modification, we construct a segment tree on the preorder walk of the tree, so that every subtree corresponds to a contiguous segment within the segment tree. This segment tree will store the contributions of each vertex and needs to support range-sum-query, range-multiply-update, and point-update (updating a single element). The details of implementing such a segment tree and are left as an exercise to the reader.

Armed with this segment tree, queries become a single range-sum. Scaling the contribution in a subtree becomes a range-multiply (we don't need to worry about multiplying un-added vertices because they are set to 0). And adding a new vertex becomes a range-sum-query to retrieve the contribution of the parent, and then a point-set to set the contribution of the added vertex.

Finally, to solve the full version of the problem, notice that the power of a non-root vertex w is a scaled down range sum in the segment tree. The value of the scale is 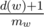, the proof of which is left as an exercise to the reader.

Time Complexity — 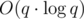, Space Complexity — O(q)

607E - Сумма пересечений

Author: GlebsHP

Code: https://ideone.com/Di8gnU

The problem boils down to summing the k closest intersections to a given query point.

We binary search on the distance d of kth farthest point. For a given distance d, the number of points within distance d of our query point is equivalent to the number of pairwise intersections that lie within a circle of radius d centered at our query point. To count the number of intersections, we can find the intersection points of the lines on the circle and sort them. Two lines which intersect will have overlapping intersection points on the circle (i.e. of the form ABAB where As and Bs are the intersection points of two lines). Counting the number of intersections can be done by DP.

Once we have d, we once again draw a circle of size d but this time we loop through all points in O(k) instead of counting the number of points.

It may happen that there are I < k intersections inside the circle of radius d but also I' > k inside a circle of radius d + ε. In this case, we should calculate the answer for d and add d(k - I).

Time Complexity — 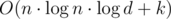, Space Complexity — O(n)