snarknews's blog

SnarkNews New Year Contests
By snarknews, history, 9 years ago, translation, In English

Traditionally, SnarkNews runs two New Year Contests.

The New Year Blitz Contest (Multiple Language Round) will start at 16:00 31.12.2015 and ends at 08:00 01.01.2016 Moscow Time. Contest will consist of 9-13 problems. Some of those problems are based on problems, used at official or training contests in 2015. Contest rules are based on the ACM system with two important modifications.

  1. Penalty time is calculated as distance between time of first successful submit for the contestant on this problem and 0:00:00 01.01.2016, i.e. successful submissions at 23:50:00 31.12.2015 and at 0:10:00 01.01.2016 will both have penalty time 10 minutes (600 seconds).

  2. Multiple Language Round rule: If for the first successful submit for the contestant on the some problem was used the programming language, which was never used by this contestant in his previous first successful submits on other problems, contestant receives language bonus: his summary penalty time is decreased by 100 minutes (6000 seconds). Note that different implementations of the same language are counting as same language, i.e. Java 6 and Java 7 are both counted as Java, C++ 32 bit and C++11 64 bit both as C++. Additionally, C and C++ are counted as same programming language.

Contest will be running on Yandex.Contest system. Link for registration and participation.

12'th Prime New Year Contest will start at 0:00 30.12.2015 and finish at 23:50 10.01.2016 Moscow time. Traditionally, Prime New Year Contest consists of problems, which were presented at team programming contests in 2015 and never solved on the contest. For the Prime New Year contest plain ACM rules are used.

Idea of Prime Contest was first implemented by Andrey Lopatin and Nick Dourov at Summer Petrozavodsk training camp at 2003; in Russian word "Prostoj" used in meanings "prime" and "easy", so, contest was called "Prostoj contest" but was composed of extremelly hard problems, numbered with prime numbers (2,3,5 etc). Since then such a numeration is traditionally used for contests, consisting of very hard problems only.

Contest will be running on Yandex.Contest system. Link for registration and participation.

Both contests have English statements.

  • Vote: I like it
  • +112
  • Vote: I do not like it

Comments Comments (22)
| Write comment?
»
9 years ago, # |
  Vote: I like it -6 Vote: I do not like it

"will start at 16:00 31.12.2015 and ends at 08:00 01.01.2016" — that is cruel...

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it -75 Vote: I do not like it

    Yes. I don't understand why to downvote your comment! It's stupid to do a contest in NEW YEAR!

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +51 Vote: I do not like it

Bump?

10 programming languages. I did well.

→ Reply
»
9 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Can people share their solutions or give hints on how to solve the problems of the MLR blitz?

I am particularly interested in the solutions of problems A, B, D, I, J, K

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 3   Vote: I like it +10 Vote: I do not like it

    A: https://en.wikipedia.org/wiki/Eight_queens_puzzle

    B: instead of making reflection continue moving in the flipped (horizontally or vertically, depends on contacting border) board. So the movement of the ball is a straight line. We should check if point ( ± xc + 2x1kx,  ± yc + 2y1ky) lies on this line for some integers kx and ky.

    I: if initial number is odd and removing last digit keeps it odd then Second player wins. Otherwise game continues until string is empty.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it +5 Vote: I do not like it

      N can be up to 200. How is that wiki enough? Am I missing something?

      UPD: There is a link to a related paper on that wiki page. I wrote this too early I guess.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 2   Vote: I like it +5 Vote: I do not like it

        There is section with Explicit solutions.

        My solution uses the following order of columns in backtracking search and finds solution faster than 10ms:

        bool fl = n % 12 == 3 || n % 12 == 9;
for(int i=1 + fl * 2; i < n; i += 2) p.push_back(i);
if(fl) p.push_back(1);
int k = p.size();
for(int i=0; i < n; i += 2) p.push_back(i);
if(n % 12 == 2) {
    swap(p[k], p[k+1]);
    for(int i=k+2; i + 1 < (int)p.size(); ++i) p[i] = p[i+1];
    p[p.size() - 1] = 4;
}
        → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        I noticed the modification for N odd; for N even, I wrote a bruteforce that tries placing (in all possible ways, always placing the first one in the leftmost free column) two sequences of queens with distances (2, 1) + a center-symmetric complement and picks one that works. It's O(N3) or O(N4) with a good constant.

        → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      It seems I've understood wrong the problem I, can somebody answer how to solve the following problem?

      "We have a string of N  ≤ 104 decimal digits (0 — 9). If the number represented by the string is even we must choose one digit and remove it. Two players play and alternate turns. The loser is the one who can't make a move. Who is the winner?"

      → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    K: the next integer position to move to from (x, y) is (x ± 1, y + R) or (x, y + 1), so if you use coordinates x' = y - Rx, y' = y + Rx, then you can move from cabbage (a, b) to any cabbage (c ≥ a, d ≥ b) and the borders don't matter — can you solve this standard problem?

    B: mirroring trick — imagine that the table is mirrored over its borders an infinite number of times, making a grid of mirrored rooms; if you know the parity of mirroring in x- and y- directions, you reach a condition of the form Ak + Bl = C for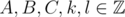

    D: just write a condition for touching, extract a quadratic equation for time when it happens, pick the right solution, sort out some cases with negative times etc.

    I: write the winning/losing positions for small numbers of digits, think; it's very simple

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Your explanation for D is actually the solution for C (the collision of two spheres), can you tell how you solved D (it is something like a modified cost edit distance)?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Oh ok. We know the cost of any common subsequence. since we know what should be added and removed; it's best to add/remove as many letters at once as possible. My algorithm is just a modification of LCS.

        → Reply
»
9 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Firstly, I would like to bring this post into recent actions. Prime New Year contest is one of not many great opportunities to challenge oneself against really hard and entertaining problems. Judging from number of submissions, I think that it gets much lower attention than it deserves.

And on a second note, I have to admit that I was very amazed when I saw problem "Solar lamps" which I have authored :). Originally it was posed as problem on POI, but concluding from its presence here — it was passed to Russia and used on some ACM contest. I think that it's too easy for that contest, fact that I am the only one who has solved it so far surprises me even more :P (of course I had prewritten solution).

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    It was used at Spring Training camp in Urozero (something like "mini Petrozavodsk" in March for finalists from Northern Subregional of NEERC; last year it had mirror in MIPT), problemset was called "Warsaw U Selection". It was supposed to be used in Petrozavodsk Winter Camp 2015, but unluckly, teams from other Polish universities were familiar with some problems.

    Btw, there is another problem in Prime Contest from this problemset. And for OpenCup not so much luck for Prime Contest in this year: at current season teams show great performance and we have no unsolved problems for all 8 contests.

    → Reply
»
9 years ago, # |
← Rev. 6   Vote: I like it 0 Vote: I do not like it

EDIT: Here was something which is not currently valid

OK, it looks like something is wrong with my program, out of the blue exactly the same code which was successfully executing both on ejudge and on my computer started to spit out some errors and nans. Let me investigate it, it's not a typical situation for me to search for bugs in programs which got AC :).

EDIT2: OK, ACed -_-..... This task will definitely haunt me for ages. What I was dealing with when making it pass both on ejudge and yandex was without a doubt the most treacherous and one of most nerves-destroying things which I have encountered in my long competitive programming experience :P.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How did you solve it?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Assume that we know cdf of Taja's results. Then using some pretty easy dp in O(n2n) we can find out best strategy against that fixed cdf. However we do not know Taja's permutation of dices, so I tried to estimate that cdf using information form so far retrieved results (for every score, how many times I lost and won). That cdf can be guessed using many different approaches and really slight changes can change getting OK into getting WA on 1st test. So proceed using that algo:

      while(!GotOK()) {
  TryDifferentWayOfEstimatingCdf();
}

      Here's my code for reference: http://ideone.com/SsFW3X (it's not typical to me, but some names of variables express my frustration during all diferent troubles I had when I was solving it :P, I will better not describe those :P)

      Were you the one to solve all problems in your team? What is the solution to 23. problem? (Marcin_smu got it ACed but that doesn't mean that we know how to solve it :P) Have you solved 31. without reading any papers? As far as I know it has a very hard and long solution (I mean description of algo, not code) which can be found here: http://www.sciencedirect.com/science/article/pii/0001870874900310

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      What about 23 problem :)? I know that if all dp's are different then all guys are comparable, so comparability graph is a tournament and there exists a hamiltonian cycle in every strongly connected tournament, so answer are exactly guys which create last SCC, but if there are guys with equal dp and close hp we get some draws and we lose that structure and I don't know how we can proceed.

      → Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

After my another nerve-destroying struggle that problemset fulfills all conditions of an ideal problemset:
1) Every problem is solved
2) Nobody has solved all problems
3) Everybody has solved at least one problem
:)

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Good job!

    Just curious, did you see the problem 2 before, or did you solve it from scratch?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +15 Vote: I do not like it

      Thanks :). I haven't seen problem 2 before, however I really like all kinds of math/combinatorial counting problems, so after reading it I fell in love at first sight with this problem and I had to solve it :P.

      → Reply
»
9 years ago, # |
  Vote: I like it -8 Vote: I do not like it

Since I have already described that before, here's a description of solar lamps solution without any heavy data structures if anyone is interested:

Firstly, using some cross and dot products, let's reduce our problem to one where those angles are determined by (0, 1) and (1, 0) (it may be troublesome when angle given in description has zero degrees, but it can be handled well without any if for that case).

Let's start with determining output for just one fixed lamp. We can simply binary search an answer and for a fixed moment in time by using sweeping line we can determine all lamps which are lit at that moment, so we have solved that easier version in O(n log^2 n). In fact, we get information which lamps are lit at moment t and if a lamp is not lit at this moment, we also know exact number of lit lamps which illuminte it and that is powerful info, because that let's us call recursively to two time intervals [1, n/2] and [n/2 + 1, n]. To first half we put all lamps that were lit at moment n/2 and to second half we put all lamps which were non lit at n/2, but we update their k_i numbers by subtracting number of lamps illuminating them at moment n/2. That division may be far from "half of lamps there, half there", but since we are dividing time by two, that recursion still has logarithmic depth and on a fixed level, fixed lamp is present in exactly one call, so on a fixed level we need O(n log n) work, so overall complexity is O(n log^2 n).

→ Reply