flash_7's blog

Interesting Number Theory Problems
By flash_7, history, 9 years ago, In English

Need help with this two number theory problems.Give me some hints please.

Problem 1:

Given an integer N <= 10^25000 find the smallest m <= N such that m/phi(m) is maximum. Where phi is euler's totient function.

Input:

The first line in the input gives the number of test cases T (T<=200), and then T lines follow each containing an integer N.

Output: Output the smallest required value of m.

Sample Input:

1
10

Output:

6

Problem 2:

You are given two integers: n and k, your task is to find the most significant three digits, and least significant three digits of n^k.

Input:

Input starts with an integer T (≤ 1000), denoting the number of test cases.

Each case starts with a line containing two integers: n (2 ≤ n < 2^31) and k (1 ≤ k ≤ 10^7).

Output:

For each case, print the case number and the three leading digits (most significant) and three trailing digits (least significant). You can assume that the input is given such that n^k contains at least six digits.

Sample Input:

5
123456 1
123456 2
2 31
2 32
29 8751919

Sample Output:

Case 1: 123 456
Case 2: 152 936
Case 3: 214 648
Case 4: 429 296
Case 5: 665 669
  • Vote: I like it
  • -12
  • Vote: I do not like it

»
9 years ago, # |
← Rev. 3   Vote: I like it +1 Vote: I do not like it

For problem 1, I think M = (max. highly composite number <= N) but don't know how to do it with biginteger values.

For Problem 2 bigmod can be used. For least significant digits MOD should be >= 1000, that will keep at least last three digits. For most significant digits double type values can be used where in place of modulo operation you can process the value so that it always keeps three digits before decimal point.

→ Reply
»
9 years ago, # |
  Vote: I like it +11 Vote: I do not like it

For the first problem you must know the formula for phi(n)

Let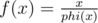

the function f(n) is multiplicative

if p|n -> f(n) = f(n * pk)

function f(p) for p a prime number is decreasing

so the answer to the problem is to find the maximum t such that

f(p1p2... pt) ≤ N which can be done efficiently (you only need the easy bignum operations)

→ Reply