VOI (Vietnam National Olympiad in Informatics) 2016 has just ended a few hours ago. You are given 6 problems (3 each day) to solve in the time of 180 minutes per day. As a contestant, I must say for such a small window of time I just couldn't do them all. Anyways here are the (of course, shortened version of) statements of the problems.

The problems have a total score of 40, which divides to 6 / 7 / 7 per day.

Day 1

Problem 1 (6 pts)

You are given a sequence of numbers A[1..n] (1 ≤ A_i ≤ 10⁹). You have to erase the least amount of numbers in the sequence such that for every i < j in the new sequence the following condition holds: .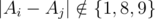

50% of the tests have n ≤ 20. The remaining have n ≤ 2000.

Problem 2 (7 pts)

There is a road which has a length of L. You have a truck with the fuel tank capacity of K, and start off with Q litres of fuel at one side (point 0) which you will have to deliver to the other side (point L) of the road. Your truck consumes 1 litre of fuel per unit of length it travels. In order to help you, starting from point 0 there is a fuel tank with unlimited capacity every D units of length (so there are tanks on point D, 2D, ... and they are empty at start). You are allowed to transfer the fuel in and out of any tank. Maximize the amount of fuel you can deliver to point L.

Given L, K, Q, D, calculate the maximum amount of fuel you can deliver to point L.

Constraints: 1 ≤ L, K, D ≤ 10⁹, 1 ≤ Q ≤ 10¹². On the first 50% of the tests .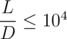

Problem 3 (7 pts)

You are given an undirected connected graph G(V, E) of n vertices and m edges (with no self edges and multi-edges) and the following algorithm to construct K:

• First, initialize K[1..n] as an array of empty vectors of integers. Let K[1] = {0}.

• Let f[1..n] be an array of booleans, all being false at start. Let Q be a set of indices i such that f[i] = false and |K[i]| > 0

• While |Q| > 0:

  • Let u be the smallest number in Q. Set f[u] = true
  • For each edge (u, v) in G such that f[v] = false we append u into back of K[v].

Please renumber all the vertices in the graph so that for the resulting array K of the algorithm the following condition holds: For every u < v we have K[u] ≤ K[v] alphabetically.

Constraints: 40% of the tests have n ≤ 10. 80% of the tests have n ≤ 10³, m ≤ 10⁴. All tests have n ≤ 2 × 10⁴, m ≤ 10⁶.

Day 2

Problem 1 (6 pts)

You are given a grid of n × m cells, each containing a zero or one. Find the diamond-shaped area (which has to be fully inside the grid) containing the most ones such that no two one cells inside the area share the same edge.

A diamond-shaped area with center (x₀, y₀) and radius r is a set of cells (x, y) which satisfies |x - x₀| + |y - y0| ≤ r.

Constraints: 40% of the tests have n ≤ 100. 80% of the tests have n ≤ 500. All tests have n ≤ 1000.

Problem 2 (7 pts)

You are given a set of n operations containing at most 4 numbers within [0..10⁶] and operators +, -, *. You have add brackets to some of the equations such that each of them has an unique value.

Constraints: 50% of the tests have n ≤ 20 and operations having at most 3 numbers. All tests have n ≤ 2000.

Problem 3 (7 pts)

You are given n trees (real world trees) with the i-th tree having height h_i and stands at position i and you have to fall down all of them. Falling the tree i to the left causes all trees j with i - h_i < j < i to fall to the left, and falling tree i to the right causes all trees j with i < j < i + h_i to fall to the right (and they to make chains like dominoes). Find a way of cutting the trees such that the number of trees manually fell at minimized.

All trees have height not exceeding 4 × 10⁶

Constraints: 40% of the tests have n ≤ 10⁴, 80% of the tests have n ≤ 10⁵, all tests have n ≤ 4 × 10⁶