615A - Bulbs (Author: TheWishmaster)
Let's make a counter of number of buttons that switch every lamp off. If there is a lamp with zero counter, output NO, otherwise YES.
code: 15260902
615B - Longtail Hedgehog (Author: TheWishmaster)
Way of solving — dynamic programming. We are given a graph of n vertices and m edges. We will calculate dp[i] — a maximum length of tail that is ending in i-th vertex. We can simply update dp by checking all the edges from i-th vertex(which are leading to vertices with bigger number), and trying to update them. When we have this dp, we can check the answer easily.
code: 15260851
615C - Running Track (Author: maxkvant)
The idea is that if can make a substring t[i, j] using k coatings, then we can also make a substring t[i + 1, j] using k coatings. So we should use the longest substring each time.
Let n = |s|, m = |t|. On each stage we will search for the longest substring in s and s_reversed to update the answer. We can do it in several ways:
- Calculate lcp[i][j] — longest common prefix t[i, m] and s[j, n], lcprev[i][j] — longest common prefix t[i, m] and s[j, 1]. Find longest means find max(max(lcp[i][1], lcp[i][2], ..., lcp[i][n]), max(lcprev[i][1], lcprev[i][2], ..., lcprev[i][n])).
calculation lcp:
for (int i = m; i >= 1; i--)
for (int j = n; j >= 1; j--)
if (t[i] == s[j])
lcp[i][j] = lcp[i + 1][j + 1] + 1;
code: 15277213
Let's check iterative t[i, i ] exists in s as a substring, t[i, i + 1] t[i, i + 2] .... We will make an array endPos, where endPos[j] is true when t[i, i + cur_len - 1] = s[j - cur_len + 1, j] (t[1, i — 1] greedy already got). We will update this array, adding symbols t[i], t[i + 1], t[i + 2] and so on. We will make one more array — for s_reversed. (more details in code)
Overall time complexity will be 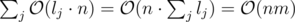
code: 15260867
trie solution: 15260870
bonus
Can you solve with 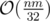 complexity?
complexity? 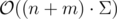 ?
? 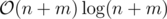 ?
?
Σ — alphabet size.
615D - Multipliers (Author: maxkvant)
Let d(x) be a number of divisors of x, and f(x) be the product of divisors. Let x = p1α1p2α2... pnαn, then d(x) = (α1 + 1)·(α2 + 1)... (αn + 1)
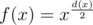 . There is
. There is 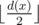 pairs of divisors of type
pairs of divisors of type 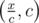 ,
, 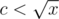 , and if x is a perfect square we have one more divisor :
, and if x is a perfect square we have one more divisor : 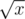 .
.
for a prime m and a ≠ 0 the statement 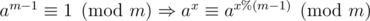 (little Fermat theorem)
(little Fermat theorem)
We can see that 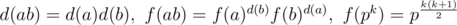 , if a and b are co prime.
, if a and b are co prime.
Now we can count the answer:
d = 1;
ans = 1;
for (int i = 0; i < l; i++) {
fp = binPow(p[i], (cnt[i] + 1) * cnt[i] / 2);
ans = binPow(ans, (cnt[i] + 1)) * binPow(fp, d) % MOD;
d = d * (cnt[i] + 1) % (MOD - 1);
}
code: 15260890
bonus
Another problem.
Given secquence (p1, k1), (p2, k2), ..., (pn, kn)
(pi — distinct primes) and q queries (l, r) to calculate f(plkl·pl + 1kl + 1... prkr)%MOD.
Can you solve with 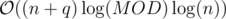 complexity?
complexity?
Suppose r - l + 1 = M = const in all queries. Can you solve with 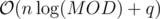 complexity?
complexity?
615E - Hexagons (Author: TheWishmaster)
Let's see how the coordinates are changing while we move from current cell to one of the 6 adjacent cells — let's call this 6 typed of moves. If we know the number of moves of each type on our way, then we know the coordinates of the end of the way. We will divide the way into rings.
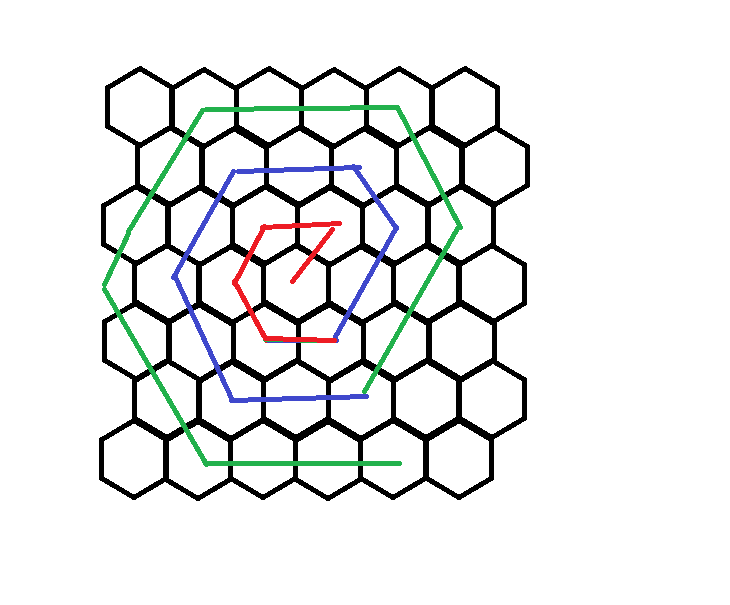
Let's count the number of moves of each type for the first ring. Next ring will have one more move of each type. Length of each ring = length of previous + 6. It is an arithmetic progression. Using well-known formulas and binary search we calculate the number of the last ring and overall length of previous rings. Now we have to brute-force 6 types of the last move and calculate the answer.
code: 15260879










I didn't realize the answer is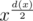 when x is not a perfect square and
when x is not a perfect square and 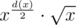 otherwise. I solved it by calculating the answer for each individual prime power :
otherwise. I solved it by calculating the answer for each individual prime power :
Let the number be p1α1·p2α2...·pkαk. Now, consider an individual prime pi. What is it's power in the final answer? It's pi(1 + 2 + ... + αi)(α1 + 1)(α2 + 1)...(αi - 1 + 1)(αi + 1 + 1)...(αk + 1). We need to find this value for every prime divisor of the number and multiply them together.
Firstly,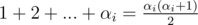 . Thus, we can calculate the sum in O(1). Note that in order to calculate
. Thus, we can calculate the sum in O(1). Note that in order to calculate 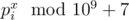 , then it is enough to take x as its remainder when divided by 109 + 6. Indeed, it is well-known that 109 + 7 is a prime. Then, by Fermat's Little Theorem,
, then it is enough to take x as its remainder when divided by 109 + 6. Indeed, it is well-known that 109 + 7 is a prime. Then, by Fermat's Little Theorem, 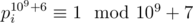 , since pi is not divisible by 109 + 7. Thus, we need to first find the exponent of the expression modulo 109 + 6.
, since pi is not divisible by 109 + 7. Thus, we need to first find the exponent of the expression modulo 109 + 6.
We can easily reduce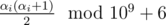 . However, how do we calculate (α1 + 1)(α2 + 1)...(αi - 1 + 1)(αi + 1 + 1)...(αk + 1)} fast? Let P = (α1 + 1)(α2 + 1)...(αi - 1 + 1)(αi + 1)(αi + 1 + 1)...(αk + 1)}. This number is independent of i, so we can calculate it (mod 109 + 6) in O(k). However, the product we want is P·(αi + 1) - 1. How do we calculate the inverse of a number modulo a number? First, we do it for when the modulus is prime. It is well-known that any number (1, 2, ..., p - 1) has a unique multiplicative inverse modulo p, for some prime p. Now, by Fermat's Little Theorem, x - 1 ≡ xp - 2 mod p, so we can find x - 1 by calculating xp - 2 (in O(logp) using exponentation by squaring). Now, sadly, 109 + 6 isn't a prime.
. However, how do we calculate (α1 + 1)(α2 + 1)...(αi - 1 + 1)(αi + 1 + 1)...(αk + 1)} fast? Let P = (α1 + 1)(α2 + 1)...(αi - 1 + 1)(αi + 1)(αi + 1 + 1)...(αk + 1)}. This number is independent of i, so we can calculate it (mod 109 + 6) in O(k). However, the product we want is P·(αi + 1) - 1. How do we calculate the inverse of a number modulo a number? First, we do it for when the modulus is prime. It is well-known that any number (1, 2, ..., p - 1) has a unique multiplicative inverse modulo p, for some prime p. Now, by Fermat's Little Theorem, x - 1 ≡ xp - 2 mod p, so we can find x - 1 by calculating xp - 2 (in O(logp) using exponentation by squaring). Now, sadly, 109 + 6 isn't a prime. 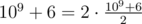 . Miraclously,
. Miraclously, 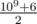 is a prime, so we can in fact compute P·(αi + 1) - 1 modulo
is a prime, so we can in fact compute P·(αi + 1) - 1 modulo 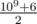 . Now, we want the exponent modulo 109 + 6. So, we need to figure out whether the product is even or odd. If at least 2 of the ais are odd, then the product is clearly even. Similarly, if all ais are even, the product is clearly even. If exactly one ai is odd, then if we calculate the prime power for pi, the product is odd, else it's even. Now, we can now use Chinese Remainder Theorem to find P·(αi + 1) - 1 modulo 109 + 6. Combining with (1 + 2 + ... + αi) finally gives us the exponent of pi modulo 109 + 6. Now, it remains to use Exponentation by Squaring to determine the desired prime power and multiply the prime powers for all prime factors of the number.
. Now, we want the exponent modulo 109 + 6. So, we need to figure out whether the product is even or odd. If at least 2 of the ais are odd, then the product is clearly even. Similarly, if all ais are even, the product is clearly even. If exactly one ai is odd, then if we calculate the prime power for pi, the product is odd, else it's even. Now, we can now use Chinese Remainder Theorem to find P·(αi + 1) - 1 modulo 109 + 6. Combining with (1 + 2 + ... + αi) finally gives us the exponent of pi modulo 109 + 6. Now, it remains to use Exponentation by Squaring to determine the desired prime power and multiply the prime powers for all prime factors of the number.
Really good solution!
As for calculating (a1 + 1)(a2 + 1)...(ai - 1 + 1)(ai + 1 + 1)...(an - 1 + 1)(an + 1) fast, I think there's a more straight forward way to do this.
All you need is prefix and suffix multiplication of (ai + 1) ,which can be solved in O(MAX_PRIME), like what I did in my code(lmul[] for prefix multiplication, rmul[] for suffix multiplication)
Now, if you want to find out (a1 + 1)(a2 + 1)...(ai - 1 + 1)(ai + 1 + 1)...(an - 1 + 1)(an + 1) ,all you need is
My code:15262736
Ah I see, I did it the hard way lol. Looks like pressure of the contest took over me.
Hi, why do you use MOD-1 instead of MOD?
Hey ariel.nowik, I suggest you read the parent comment of zscoder again because what I am going to tell is already mentioned in it.
Fermat's little theorem tells that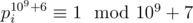
i.e., any prime raised to MOD-1 is congruent to 1 modulo MOD, since MOD is itself a prime number.
I hope you figure rest of it out.
Thank god, I also came with this solution but I have no idea how to handle 10^9+6. Thanks a lot, it has been bothering me for an hour.
On problem B, in this statement: 3. The numbers of points from the beginning of the tail to the end should strictly increase.
With this statement, Do you want to say that the number that identifies each vertex must strictly increase? Or that the quantity of vertices should increase?
For me its ambiguous. Sorry for the bad english and thanks for the contest i had fun.
The number that identifies each vertex must strictly increase. because "quantity of vertices should strictly increase"- what does that even mean?
It means that the quantity of vertices on the tail should increase. But now after your comment i see that i was confusing. This interpretation make sense but is completely useless. Thanks.
I was confused too...but quantity seems much stranger...
you mean strange?
Yes...How to define "the quantity of a vertice"?
the quantity of vertices — the total number of vertices.
But it can't be defined to each vertice...
Did anyone manage to get AC with hashing? I got TLE on case 16 :(
I was TLE on case 19...
is there anyone? Help me why my code wrong answer(after 20th). I think if there are 2, 2, 3, 3, 3
At first, I calculated total combination using given prime. Using above example, there is 2 and the count of 2 is three. and there is 3 and the count of 3 is four. So, the total is 3 x 4 = 12
When calculating the answer, each given prime can sue the total combination with division For example, I get the total combination 12 So when calculating 2, the number of 2 is three, therefore '2' can appear 12/3 = 4.
In this process, the result is below
(2x4) x (4x4) x (3x3) x (9x3) x (27x3)
ll prime[200100]; ll total = 1; ll mod = 1e9 + 7; ll ans = 1; int n;
ll power(ll a, ll b){ ll val = 1; while (b){ if (b & 1) b--, val *= a; a *= a; b >>= 1; a %= mod; val %= mod; } return val; } int main(){ //freopen("input.txt", "r", stdin); cin >> n;
for (int i = 0; i < n; i++){ ll p; cin >> p; prime[p]++; //cocunt the number of prime 'p' } for (int i = 0; i <= 200000; i++){ total *= (prime[i] + 1); //calculate the whole possible combination total %= mod; } for (ll i = 1; i <= 200000; i++){ if (prime[i] != 0){ // a/b (% p) = a * b^(p-2) % p ll val = i; ll pw = power(prime[i] + 1, (mod - 2)); //pw is b^(p-2) ll comb = (total * pw) % mod; for (ll c = 1; c <= prime[i]; c++){ ll next = power(val, comb); ans = (ans * next) % mod; val *= i; val %= mod; } } } cout << ans; return 0;}
I did a little more analysis on B(although the solution is almost same).
Create a directed graph with edges going from higher to lower number. Now the Graph cannot have cycles just because it will disprove the definition of the graph.
Now since the Graph is a DAG we can easily apply DP on graph to take out: f(x) — the longest chain ending at x now answer is maximum of f(x) * out_degree[x]
The acyclic states was kind of unclear to me which took me time to solve it..
My solution to problem C: http://mirror.codeforces.com/contest/615/submission/15266012
Let rs be string s reversed. We find the longest prefix of t that is present in s or in rs, then we remove the suffix from t and repeat until t is empty. If the size of the suffix at some point is zero, then the answer is -1. One way to find such suffix is to do a binary search and get the longest suffix that is present in either s or rs.
Time complexity: O(|s||t+s|log|t|)
i made something similar, i builted two suffix arrays and then i did a binary search on the suffixs for getting the maximum substring. But i removed the prefixs from t until t is empty.
I find string problems too hard to solve. Could you please recommend any online courses/tutorials ? Thanks
Can anyone explain why in problem D answer is calculated as ans = binPow(ans, (cnt[i] + 1)) * binPow(fp, d) % MOD; instead of ans=ans* binPow(fp, d) % MOD;
Firstly, your way to calculate answer doesn't work on test:
f(ab) = f(a)d(b)f(b)d(a), if a and b are co prime.
proof:
f(x) = xd(x) / 2
f(ab) = (ab)d(ab) / 2 = (ab)(d(a) d(b)) / 2 = = (ad(b) / 2)d(b)(bd(b) / 2)d(a) = f(a)d(b)f(a)d(b)
Problem C: I didn't understand this line:
"Now we will make an array endPos, where endPos[i] is true when t[i, i + cur_len - 1] = s[i - cur_len + 1, i]. We will update this array, adding symbols t[i], t[i + 1], t[i + 2] and so on."
what is cur_len? How to find cur_len? "adding symbols t[i], ... so on." where are we adding what? and how to use endpos to get the final answer?
Please someone clarify it in details!
Added another solution and updated old. Is some solution clear?
In problem B what if there was a shorter path with very high number of spines so when we multiply with number of spines the final result of the shorter path is bigger than the longest path?
we are checking from each point the longest possible tail possible with that point as endpoint multiplied by the spines. So that case is handled there
Problem D and E were really cool problems :) Though I messed up D in contest time and couldn't check E then :( But I solved E in one try and D just after the contest :'( It could have been a really good contest for me :(
Could u pls explain how u calculated vertex number.. After calculating ring number.?? I get that the 6 adjacent edges of each cell progress in a similar manner..however how is that generalized to calculate the offset from the starting position of the ring in which the answer vertex lies?
as the arithmetic progression is 6(1+2+3+...), so I found out for which integer x 3*x*(x+1)<=n and 3*(x+1)*(x+2)>n. then I subtracted it from n. now the rest of the moves will make a partial ring. as every ring has 6 sides and and every side has x moves now, I again divided the remaining moves by x and found out on which side the last move will be. then I just wrote 5/6 cases for each side it can be on.
Is there anyone attempt to solve Problem C with hash? I tried this, I think the complexity is about O(n^2) after I use unordered_map in c++11. However, It still takes too much time and got TLE.
I find the longest common segment in string s in this way: calculate all n^2 segments(inverse order included) hash value and stored them in unordered_map. The key in unordered_map is hash value of some segment, the value is the segment id. My code is 15269449. Could anyone tell me why TLE happened? Thank you
hi in 615D — Multipliers solution
d = d * (cnt[i] + 1) % (MOD — 1); why add (MOD-1) not MOD
Reason :
Assume d is the exponent for i, i.e. i with appear in the final product d times.
According to Fermat's little theorem, (ab)%mod = ((ab%(mod - 1))%mod) if mod is a prime number and not the other way round.
This if I say i will appear in the final product d times modulo M, then it is safe to assume that i will appear in the final product d%(M - 1) times modulo M.(if M is a prime)
And in this problem, M is a prime number i.e. 109 + 7.
d(4) = 3 , divisors (1,2,4) d(6) = 4 , divisors (1,2,3,6) d(4*6)= 8 divisors (1,2,3,4,6,8,12,24)
d(4*6) not equal d(4)*d(6)
d(4) = 3 , divisors (1,2,4) d(6) = 4 , divisors (1,2,3,6) d(4*6)= 8 divisors (1,2,3,4,6,8,12,24)
d(4*6) not equal d(4)*d(6)
,,edit , i got it ,, a and b should be coprimes
A simpler solution with less math for D:
We need to calculate $$$n^ {\frac{d}{2}} \bmod p$$$ where $$$d$$$ is the count of divisors of $$$n$$$ (this is actually still true even if $$$d$$$ is odd).
And as we all know, if $$$n = p_1^{a_1} \times p_2^{a_2} \times \ldots \times p_k^{a_k}$$$ then $$$d = (a_1 + 1) \times (a_2 + 1) \times \ldots \ (a_k + 1)$$$.
If any of $$$a_i$$$ is odd then we can divide the first $$$a_i + 1$$$ by 2 and then calculate normally.
Else every $$$a_i$$$ is even, i.e. $$$n$$$ is a square number, and we can use this fact to remove the $$$/2$$$ from $$$d/2$$$. Let $$$n = x^2$$$, then $$$n^\frac{d}{2} \Leftrightarrow (x^2)^{\frac{d}{2}} \Leftrightarrow x^{2\times \frac{d}{2}} \Leftrightarrow x^d$$$.
My (not so clean) implementation: 161385006.
Can you plz explain why you first odd ai+1 divide by 2? how it work if we divide by 2. Thanks.
So we need to calculate $$$n^ {\frac{d}{2}} \bmod p$$$ where $$$d = (a_1 + 1) \times (a_2 + 1) \times \ldots \ (a_k + 1)$$$.
The problem here is $$${\frac{d}{2}}$$$. If $$$d$$$ is odd, then it will be hard for us to calculate, but $$$d$$$ is odd only if all $$$a_i + 1$$$ is odd, which means all $$$a_i$$$ is even, then $$$n$$$ is a square number and ... (like my explanation above).
So now, $$$d$$$ is even, and we can find some $$$a_i + 1$$$ that is even, then $$$d = (a_1 + 1) \times (a_2 + 1) \ldots \times ((a_i + 1) / 2) \ldots \times (a_k + 1)$$$.
Hope that makes sense.
Now it's clear for me. Thanks a lot.