gXa's blog

Running time of Algo
By gXa, history, 9 years ago, In English

We have designed an new algorithm to sort a list of n numbers. We recursively partition the numbers into groups of size sqrt(n) each until we are left with lists of constant size; at which point we use insertion sort to sort the numbers. To combine solutions, we do a merge of the sorted lists, namely maintaining pointers to the start of the list and at each step advancing the pointer of the list corresponding to the smallest element. Let T(n) denote the running time of this algorithm (we can assume that sqrt(k) is an integer for all k<=n encountered in the algorithm).

Running time : T(n) <= sqrt(n) T( sqrt(n) ) + O(n^1.5)

I can think of it as T(n) = T( sqrt(n) ) + T( n-sqrt(n) ) + O(n) but can't relate to the solution. Plz can anybody explain its running time.

  • Vote: I like it
  • -13
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

We recursively partition the numbers into groups of size sqrt(n) each until we are left with lists of constant size

If I understand it correctly, you decide a constant k and then recursively split the lists until all of them are at most k long. If instead of you decide to split in half, then the running time would be . However, since you split in , the running time will be less than that. Not that it's better, since you could just split it in lists of size  ≤ k in time O(n).

at which point we use insertion sort to sort the numbers

Which is O(k²) repeated for O(n / k) lists, so: O(kn).

we do a merge of the sorted lists

Which means comparing at each step O(n / k) numbers, choosing the smallest, and advancing its pointer. The steps will be O(n) of course, so the running time of this will be: O(n² / k).

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Actually I am not getting running time given in bold. How O(n^1.5) comes? So can u plz elaborate that?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      The algorithm is not O(n1.5), it's O(n2) because of the expensive "final merge" as I explained in my comment.

      If you're asking what n1.5 means, well, that notation is another way of saying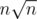 , because .

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it -8 Vote: I do not like it

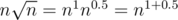        Still I can't get how ur above relation O(n² / k) relates to Running time : T(n) <= sqrt(n) T( sqrt(n) ) + O(n^1.5).

        Plz can u explain how one reached over this running time.

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Oh, you mean that the "Running time" indicated in the OP is the expected solution. Ok, I will post another comment and try to explain it. My first comment comes to the solution using a different method (not a recurrence relation).

          → Reply
          • »
            »
            »
            »
            »
            »
            9 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Ok waiting for the solution.

            → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Define T(n) as the running time of the sorting algorithm.

Say you have n = 256 elements. You can compute T(256) like this:

  1. Split the array in 16 lists (each one of them of size 16) and solve them recursively
  2. Sort the 16 lists
  3. Merge the 16 lists

Now, the first step is clearly: T(16) + T(16) + ... + T(16) for 16 times. That is: 16T(16). That is: .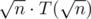

The second step is: 162 + 162 + ... + 162 for 16 times, or better: 256 + 256 + ... + 256 for 16 times. That is: 16·256. That is: .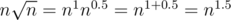

The third step is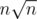 as well, because you have to repeat n times the "select the minimum and advance its pointer" method, and that is alone (because there are lists).

At the end, the recurrence relation is: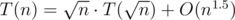

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks a lot, extremely nice explanation.

    → Reply