Ответа на комментарий по задаче так и не получил, поэтому перепост.
Мне кажется, для любых a и t верно утверждение
если
Это связано с тем, что в последовательности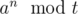
предпериод не превосходит степени максимального простого в t, а период после разложения t = t1t2 на часть t1, взаимно простую с a и все остальное будет совпадать по длине с периодом 
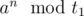, делителем 
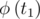, делителем 
Мне кажется, для любых a и t верно утверждение
если
Это связано с тем, что в последовательности
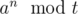предпериод не превосходит степени максимального простого в t, а период после разложения t = t1t2 на часть t1, взаимно простую с a и все остальное будет совпадать по длине с периодом 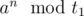, делителем 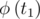, делителем Прошу доказать строго или опровергнуть.
Примитивной программой проверил до t <= 100, n < t*4, работает.
Как использовать этот факт, если это верно?
Например, расчет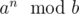 
быстрым возведением в степень требует либо представления числа n в двоичной системе счисления, либо использования десятичного возведения в степень с плохой константой. При ограничениях a, b ≤ 106, n ≤ 1010000000 быстрое возведение в степень невозможно.
С уточнениями от freopen
pow(a,b):
res=1
if (b>=10) res=pow(a,b/10);
res=res*res*res*res*res*res*res*res*res*res;
for (i=0;i<b%10;i++) res*=a
return res
Это понятно. Можно и в двоичную число длиной 100к знаков за секунду-другую перевести.
В любом случае, взять остаток от степени явно быстрее на порядок.
2. Почему делить длинное на короткое быстрее, чем вообще решение без длинки?
2. Указанное быстрое возведение в степень требует 19 умножений и делений 64-битных чисел на разряд N.
Деление длинного на короткое потребует 1 умножение и деление 32-битных чисел на разряд N. От умножения, при желании, можно избавиться.
1. Надо проверять. Для задачи дьявольская последовательность на Тимусе я сдавал решение, которое за 0.421 секунды вычисляло значение (2/3) * (1/2)^N для N <= 100000 c точностью 30000 десятичных знаков.
Поправка: 0.14 секунды на настоящий момент.
Деление с кучей оптимизаций.
Сейчас на моем компьютере на перевод 10^5 надо 829мс.
На запуске сервера CF - 600мс.
Фактически, перевод осуществляется в систему счисления с основанием 2^21 из системы счисления с основанием 10^3.
Это понятно.
Вообще, дискуссия ушла в сторону. Если оригинальное утверждение верно, то решение будет еще проще и намного быстрее работать.
an ≡ an - c (mod t)
an - an - c ≡ 0 (mod t)
an - c(ac - 1) ≡ 0 (mod t)
То есть произведение в левой части сравнения делится на t. Сами множители этого произведения взаимно простые (думаю, понятно почему). То есть, если в факторизации t есть какие-то простые, которые присутствуют в факторизации a, то единственный способ «покрыть» эти простые — набрать достаточно большую степень an - c. Понятно, что если показатель этой степени превосходит логарифм t по основанию 2 (наименьшее простое число), то этот множитель обязательно будет делиться на t2 (в вашей нотации).
С простыми в t2 мы уже «справились», и нам известно, что второй множитель в левой части сравнения не имеет простых делителей, общих с t2. Тогда нам осталось найти c:
ac - 1 ≡ 0 (mod t1)
a и t1 взаимно просты, а значит выполняется условие теоремы Эйлера.
Сойдет?
Проверьте отдельно для примарных сомножителей в разложении t (либо взаимно простых с a, либо нет).
P. S. Первая правка радует.
Кажется, при обновлении сервера что-то с tex-ом приключилось.
Идея в том, что a^b == a^{b - \phi (n)} (mod n) при b >= 2 \phi (n)