john_hopes's blog

Numbers less than X of a range in an array
By john_hopes, history, 9 years ago, In English

You'll be given an Array of N elements and Q queries.

Here N and Q is a non-negative integer and maximum value of N and Q is 100000.

There are two types of query.

One is : 1 P V , this means that you have to change P-th element of the array to V.

Another is : 2 L R X , this means that you have to output the number of elements less than or equal to X in L to R range of the array.

How can I solve this problem? I know the solution if there is no update operation. But this problem contains update operation.

Thanks in Advance. :)

  • Vote: I like it
  • +13
  • Vote: I do not like it

Comments Comments (41)
| Write comment?
»
9 years ago, # |
← Rev. 2   Vote: I like it +23 Vote: I do not like it

There is a solution with treap in every node of segment tree

→ Reply
»
9 years ago, # |
← Rev. 8   Vote: I like it +1 Vote: I do not like it

A solution is sqrt decompress. Let divide array into sqrt(N) blocks. Then sort each of blocks. Complexity O(Q * sqrt(N) * log(N) / 2). Using fenwick2d we can reduce complexity into O(Q * sqrt(N) + Q * log(N)^2) per query.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Use a persistent segment tree to maintain the initial configuration while use a BIT or segment tree to maintain the modification of persistent segment tree (notice that each modifcation is first substrcation of value of specific index in a prefix of segment trees represented by the persistent segment tree, then an addition). O(NlgN+QlgNlgN)?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    could you please elaborate more on the segment tree used to store the modifications ?

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How to handle updates?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can anybody please help me out here :(

      Is it even possible to handle updates with persistent segment tree? Nezzar

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Can't this question be done simply using merge sort tree?

        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

link to the problem please

→ Reply
»
9 years ago, # |
  Vote: I like it +11 Vote: I do not like it

There is an online solution working in O(log^2(N) per query, this should be enough if the time limit is not strict.

You can answer how many values are less than X in a binary search tree (BST) in O(logN), so create a segment tree where each node contains a BST, if the node covers interval [L, R] the BST contains all values in the interval [L, R].

To update a value just remove the old one and insert the new one in each BST in the path from leaf to root of segment tree.

To query how many values are less than X just do a query to each BST in the range (there are upto logN).

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    BST in every node? but what is memory complexity?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +20 Vote: I do not like it

      NlogN, because in every layer(depth) of segment tree you have all N elements exactly once. Segment tree depth = logN, so total memory is NlogN

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Excuse me for noob question

        but how does the merge between two binary search trees work ?

        i mean besides the obvious way of taking every node from one tree and inserting it to the other

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
          ← Rev. 3   Vote: I like it +6 Vote: I do not like it

          OK, I'll try to explain it.

          Let's keep a treap in every nodev of segment tree. This treap will contain all elements from range [l..r] — the range which node v is responsible for.

          How to add(on building stage) or modify element at position idx? Let's find all nodes which have idx in their range(it means tl <= idx <= tr; where tl, tr — borders of segment which current node is responsible for) — it is just all nodes in the path from root to some leaf with tl = tr = idx. Let's add given value in all treaps of these nodes. It is easy to modify element — just erase old values from all these treaps and then add new. Asymptotics for adding / modifying is O(log^2N): logN layers and adding number in the layer is also logN.

          How to answer for a query l, r, x? Just do everything you have done in a usual segment tree, but for a query in some node which is fully contained in [l..r] the answer is a number of elements less than x in this treap. Asymptotics is also O(log^2N) — logN nodes with logN for answering in every node

          So, it is O(Nlog^2N) for building, O(log^2N) per any query and O(NlogN) of memory

          As you could understand it is no need to merge sons' treaps(as you said)

          → Reply
          • »
            »
            »
            »
            »
            »
            9 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Why treap instead of bst ? I don't know a treap data structure, but I think that it might work using bst

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              9 years ago, # ^ |
              ← Rev. 2   Vote: I like it 0 Vote: I do not like it

              I like treaps and don't like BST :)

              → Reply
          • »
            »
            »
            »
            »
            »
            9 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Thank you so much !!

            the whole time i was trying to build from the bottom up the whole array together

            inserting element by element didn't cross my mind

            if not much trouble do you have any source for self balancing BSTs or treaps ?

            → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        can u give me some treap problem in codeforces

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Try problem E in contest 367. It's not the official solution, and may not pass all tests due to memory and / or time, but it can be done.

          → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why so many down votes ? It's really interesting problem. Please provide a link to this problem

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

how can I solve it if there are updates for ranges?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    chemthan's idea can be extended to range update and query and will work in O(N*log(N)*sqrt(N)). The difference is that you'll need a segment tree with lazy for range update in each bucket.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      chemthan's solution or kefaa's solution ?

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can you tell me the solution when there are no updates?

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I think I have an idea for an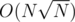 solution. It should be quite similar in speed to O(Nlog2N).

First there exists a method to maintain an array of size 100000 with update to change number at a position, and O(1) query sum within range. We can do this by splitting this array up into blocks and maintaining cumulative sums within and over these blocks. This allows us to keep track of how many things less than X are in here. Keep in mind this structure is secondary and is separate from our actual array.

Now, let's split the actual array into blocks. Each blocks holds the above structure. When we update a position, we look at the block that it is in and update it. Specifically, if we change it to some value, we update the count in the structure described. This is an update.

Now to query, we look at all the full blocks contained in the range and query each in O(1). As there are max blocks, this is total query. Next, we count each of the extra positions within the range which aren't in a full block. This is also because each block has size .

Thus we have a solution with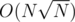 which can be easier than treap+segtree, and possibly faster due to treap constant factor.

Edit: oops I didn't realise this thread was dead >.<

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    How are you going to get the answer for a single block in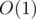 time?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      So in the first structure which I described we can get O(1) query by maintaining a prefix sum array. We keep 1. prefix sum array inside each block 2. prefix sum array over the blocks. Every time we update we can afford O(sqrt) operations so we update the cumulative sum array inside the block, and also over all the blocks (both sqrt operations).

      Now to query, we look at sum of all full blocks inside range in O(1) using prefix sum. Next, we look at sum within partial blocks using prefix sum and get the value in O(1).

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    This allows us to keep track of how many things less than X are in here.

    How can you use the prefix sums to figure out how many things less than X there are, when X is changing every query?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I'm not sure what you're asking... A regular prefix sum let's you query for every X anyway — this system is no different. You just query twice, once for big blocks, once for a partial block.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I think he doesn't understand how to query in O(1) using prefix sums. I don't understand too. How about ordering each block and use binary search to find numbers less than x? Query-O(sqrt(N)×logN) Update-O(logN). Is it too much?

        → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    nice solution

    → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Nice solution.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

alternatively, couldn't you just store an ordered_set (from gnu pbds namespace) in each node of the segment tree?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

you can use segment tree or sparse table to solve it

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

there is a solution with Merge Sort Tree.

https://discuss.codechef.com/questions/94448/merge-sort-tree-tutorial

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

This problem is almost same as SPOJ : Giveaway.

→ Reply