Просто задача на подумать.

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Я не буду просить, чтобы вы ее решили. Просто кажется интересным.

Пусть дан некоторый массив a размером N < 2³⁰ 32-битных целых чисел. Требуется выполнить M запросов вида "сумма чисел на данном отрезке" за O(N+M), используя как можно меньше дополнительной памяти.

Очевидно, что существует решение, использующее 30 * N бит дополнительной памяти.

Update 1.
Если допускать сложность O(N+M*log(N)), то можно добиться 6 * N бит дополнительной памяти.

=============

В связи с особыми шаманствами, думаю, надо формализовать задачу немного по-другому.

Пусть дан некоторый массив a размером N из β-битных целых чисел. Требуется выполнить M запросов вида "сумма чисел на данном отрезке" за O(N+M), используя как можно меньше дополнительной памяти. Операция сложения и обращения по индексу выполняются за О(1), умножение процессор не поддерживает.

Очевидно, что существует решение, использующее 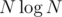$\text{[math]}$ бит дополнительной памяти.

Если допускать сложность O(N+M*log(N)), то можно добиться сколь угодно мало дополнительной памяти ценой сколь угодно большой константы во времени.

Комментарии (22)

Написать комментарий?

ivan.popelyshev

13 лет назад, # |

-8

А сами ответы выдаются в 32-битном виде, или 64 бита нужно?

→ Ответить

I_love_natalia

13 лет назад, # ^ |

Ответ, конечно, надо выдать честно. Все 64 бита.

Запросы поступают по одному. Хранение запросов, полагаю, надо считать дополнительной памятью :)

Perlik

← Rev. 2 →

Насколько я понимаю, это ни что иное, как сумма на отрезке за O(1)? Интересно увидеть решение, такого еще нигде не встречал.

PavelKunyavskiy

Предподсчитаем суммы на префиксах. На это нужно 30N бит. Сумма на отрезке - разность сумм на двух префиксах. Это вроде просто. Меньше что-то придумать не могу...

KADR	13 лет назад, # ^ \| 0 А почему 30N? Нам надо хранить по 62 бита на каждое число, что в сумме будет 62N. Числа-то до 2³²и всего их 2³⁰. → Ответить

Дополнительной памяти нужно 30N. 32N дано в начале.

Да. Но мы меряем только доп память. Сам массив нам при таком методе не нужен, да и восстановим если нужен потом. А сам массив - 32 бита на элемент.

KADR

Интересно, а как мы можем заюзать этот же массив, если у исходного типа размер 32 бита, а у результата 62? Даже если мы будем интерпритировать массив как просто последовательность битов, как мы сможем с О(1) дополнительного места превратить этот массив в массив частичных сумм?

Мы положим рядом массив старших частей.

KADR	13 лет назад, # ^ \| ← Rev. 3 → 0 Не поможет. Мы когда будем превращать наш массив в массив частичных сумм, затрем исходные данные. Пока что я вижу как за 32N дополнительной памяти это обойти. UPD: см. мой комментарий ниже. → Ответить

Это какие исходные данные затрете? Берем и слева на право пересчитываем. Просто число как бы длинное, но не массив, а пара.

KADR	13 лет назад, # ^ \| 0 А, хм. Я думал имеется ввиду положить рядом массив размера 30N и писать последовательно. А если разделить старшие 30 бит и младшие 32, то вроде можно :) → Ответить

Philip_PV

← Rev. 5 →

Ну и, очевидно, можно теперь уменьшать константу при N в выражении 62N, увеличивая константу в O(N + M) при M.

-7

Как кто-то уже написал 2:30 - тоже константа. На практике же константа будет logn, ну или log(2^32) в крайнем случае.

← Rev. 8 →

Знаете, я что Вас, что автора темы совершенно не понимаю.

Как только вы ограничиваете параметры сверху, то ни о какой O-нотации, включающей эти параметры, и речи быть не может. А тут, "как кто-то уже написал", начинается какое-то мешалово асимптотик и абсолютных значений.

UPD: в новой формулировке при фиксированной разрядности регистра, учитывая, что каждое начальное значение в массиве помещается в регистр,

сложности для RAM-машины могут, например, быть $\text{[math]}$ по памяти и $\text{[math]}$ по времени для любой функции f(N), если сохранять значения частичных сумм с шагом f(N).

UPD2: я за Вами не успеваю, я только пост отредактирую, условие уже меняется :)

Убрал в формализме все ограничения. Они и правда не нужны.

Извиняюсь за UPD2 :)

it4.kp

А почему 30N?

Вообще вопрос странный немного. Для времени работы установлено ассимптотическое ограничение, а для памяти кол-во бит. Что мешает посчитать частичные суммы блоков по L элементов, где L - константа? Памяти надо будет N/L*64, а время ассимптотически O(N+M). Понятно что если L близко к N то смысл вопроса теряется.

Urbanowicz

Учитывая, что N ограничено сверху неиллюзорной константой, то наивное решение будет оптимальным) Всего две дополнительные перемнные, а асимптотика вообще O(M).

Можно за 31/15*N бит, если mlogn. Просто честно храним ответ через каждые 30 значений. а эти 30 проходим и считаем. 6N не интересно.

← Rev. 3 →

Еще читерские способы сделать очень большую константу есть?

Если нет, можно вернуться к началу и придумать что-нибудь годное.

Для функции просеивания ответов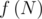 $\text{[math]}$ получаем

Время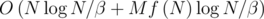 $\text{[math]}$

Память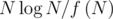 $\text{[math]}$

Таким образом, $\text{[math]}$ дает сколь угодно мало памяти при сколь угодно большой константе во времени для случая $\text{[math]}$ . ОК, ясно.

Блог пользователя I_love_natalia