Только что закончился Гран-При Саратова. Подскажите, как решать F?
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 24.11.2024 05:53:58 (i2).
Десктопная версия, переключиться на мобильную.
При поддержке
Как решать J?
1) Бинарный поиск по ответу. Пусть наш ответ равен ans — выгодно брать ans приборов с самыми большими левелами.
2) Будем строить нашу конструкцию. При постройке выгодно сначала юзать свичи с наибольшим количеством разъемов.
3) Когда мы дошли до уровня level и еще не закончили постройку — поставим туда все устройства, которые должны стоять на этом уровне (раньше ставить нет смысла).
4) В конце, когда мы поставили все свичи — возможно нужно еще какие-то устройства постаить. Посмотрим, хватит ли у нас разъемов.
http://pastebin.com/ybAei9F4
Как А нормально решать?
Я написал тупую динамику (позиция, разница между вторым и первым по величине, разница между третьим и вторым (сервера упорядочены по возрастанию суммарного времени на них), ограничив эти разницы величиной BUBEN). Такое получает ВА 188. Потом мне сообщили, что там 189 тестов и random_shuffle решает эту проблему (и дорешивание показывает, что таки решает) :(
Мы посчитали, что этот бубен равен 30*29 (нок 30 и 29). Поизвращались с сохранением в память пути и сдали без рандома (точнее сначала с ним, но потом стало скучно и сдали без него). Почему важен НОК не знаю
Вроде ж как можно закодить честный рюкзак
DP[первая сумма][вторая сумма]на битмасках. Только с восстановлением ответа придется помучатся... Там типа эти способы "стандартные", с разделяй и властвуй либо корневой.А еще можно погруппировать одинаковые элементы по 2, 4, 8... штук, это в худшем случае в пару раз уменьшает количество элементов.
Ну да, это авторское.
Можно корневой; можно разделяй и властвуй (вроде оба способа нормально заходят). Можно еще воспользоваться монотонностью и хранить таблицу дп для восстановления в виде "при каком первом значении i позиция становится достижимой".
Можно детальнее, как сделать "погруппировать"? У нас ведь два рюкзака, а не один. Там уже на втором примере, если группировать 3 одинаковых элемента как 2+1, то получить 1 в первой размерности и 1 во второй вроде не получается.
Можно брать все степени по два раза.
Спасибо, прикольная идея :)
А можно расписать подробнее, где используются битмаски? И как восстанавливать ответ?
Кстати, а кто-то отжиг сдал? Мой падает на 93-м тесте
Можно
DP[первая сумма][вторая сумма], но без битмасок за времяmaxElement * maxSum^2 = 30 * 4030^2, которая зашла за 0.58с.Код: http://ideone.com/elPSXb
Элементы d хранят в первом бите 0, если пришли туда по первой сумме, 1, если по второй, а также индекс элемента, по которому пришли, сдвинутый на 1 бит влево.
Суть в том, что можно интересным образом обрабатывать одинаковые элементы. Мы говорим, что если для того чтобы придти в данную ячейку использовалось ровно 3 раза число i, то индекс, который будет хранить эта ячейка — 3-й по счету индекс числа i во входных данных.
Как решать H?
Строим выпуклую оболочку по характеристикам ружей и на этой выпуклой оболочке делаем тернарный поиск по ответу.
Заметим, что для каждого i нужно найти j такое, что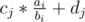
— будет минимальным.Построим нижнее огибающее множество точек для прямых cj * x + dj. Затем отсортируем запросы по 
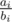. Затем с помощью двух указателей будем находить прямую, которую будет пересекать вертикальная прямая 
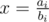. Код
Off topic: Edit your title and add "2016" to it.
Solution for F: Use extended euclidean algorithm to find solution for a1x1 + a2x2 + a3x3... = A, where x1,x2,x3 are unknowns.
What does this tell us? If x1 is positive, it means we have to fill container a1 x1 times. If x1 is negative, we have to empty a1 container x1 times.
Ultimately that should matter only. Once you know which one to fill and which one to empty, rest is simulation.
I will give an example using two containers of capacity 5 and 3. Let them be A and B. Suppose we want to make 1. Then:
5*2 + 3*-3 = 1. Therefore, we have to fill first container two times and empty second container 3 times. How do we do that?
Fill first container. Now, we have to fill it again. But it's already full, so transfer 3 units from A to B. We still have 2 units left in A. But B is already full, so we can't transfer. Then again, we have to empty B 3 times. So let us empty it once now. Then transfer 2 units to B again. Keep repeating until desired result is achieved.
Basically, those that need to be filled will get their water from outside and are not allowed to throw their water outside. Those that will empty their container will throw their water and are not allowed to get their water from outside.
We didn't get time to code it. Can somebody who got AC verify the idea?
We got AC using this approach. You should note that you can't calculate x1,x2,... simply using extended gcd algorithm because they would grow exponentially. However you can exchange xi, xj for xi'=(xi — aj), xj'=(xj + ai), so a1x1'+a2x2'+... still equals A, and using operations of this type after each run of extended gcd you can ensure |xi| <= max aj <= 2 * 10^4. Another solution is to run bfs on graph with 4 * 10^4 vertices with edges v -> v + ai, v -> v — ai and find a path from 0 to A.
Published in the Gym: 2015-2016 Petrozavodsk Winter Training Camp, Saratov SU Contest.
Так как F то решать? А то мы видимо одна команда с 8 без нее :) И даже идей особо кроме какого то паленого перебора не было :)
Мы сдали вот что, доказывать не умеем.
Скажем, что в каждый момент нас интересует только одно ведро и уровень воды в нём. Остальные вёдра либо пустые, либо полные, не важно. Состояние -- [vessel_id, amount]. Переходов три или четыре, типа "нальём из другого ведра, пока не перельётся", "выльем в другое ведро, пока оно не заполнится" и т.д. (деталей не знаю). Дальше по этим состояниям запускаем поиск в ширину.
Известный алгоритм:
Пусть у нас есть два ведра a, b, тогда можно получить любое значение в большем ведре, кратное gcd(a, b).
Алгоритм: наливаем в маленькое, переливаем в большое, если оно наполнилось, то выливаем. мы будем получать значения a, 2a % b, 3a % b, etc
Наша задача: Отсечем тупые случаи(не кратно gcd, больше максимума).
Отделим ведро-максимум M от остальных a_1,..a_k Будем аналогичным алгоритмом наливать в a_k переливать в M, пока в нем не станет x % g == a % g, где g= gcd(M, a_1, a_2 ..., a_{k-1}), после этого повторим с оставшимися ведрами. В конце получим x % g == a % g , g = M, что и нужно.
Минимизировать не просили, операций получается если грубо оценивать как раз порядка 2e4 * 10 * (3-4)
how to solve K?
Где можно дорешать Div2?
Хотелось бы понять, как решать I. Вроде бы для этого нужно уметь быстро находить mex на интервале, но как это делать онлайн?
Заметим, что запросы всегда от какой-то позиции и до конца. Строим дерево отрезков на минимум, в котором поддерживаем для каждого числа позицию самого правого на данный момент вхождения. Тогда отвечать на mex можно либо поиском по дереву (NlogN), либо бинпоиском и простым запросом на минимум (N(logN)^2). Не проверял, лезет ли последнее в TL.