Hello all,
Today I will bring you some interesting problem: Oh, I forgot to mention I cannot solve it...Dx
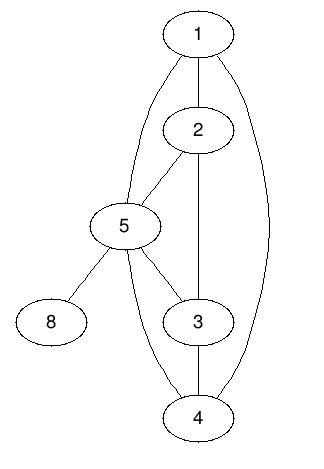
So here is the problem. I guess I have some observation: that we have to consider the cycles in the graph. For example, in this graph here, we have 4 regions, and each region has an edge the other regions don't use. (Regions are coloured)
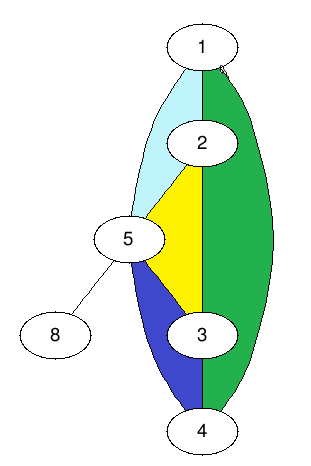
However, if I put new node 9 here, and try to colour like this:
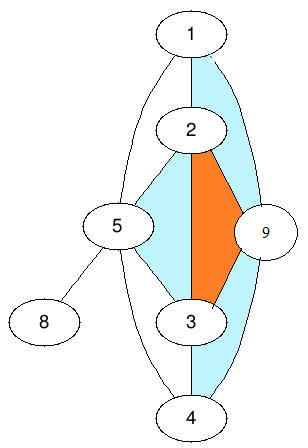
But look it the problem here: if we try to use all 3 blue loops, then we cannot use the orange loop. So there is something tricky here.
So if anyone has any ideas or can provide some hints, I would really appreciate!
Thanks,
minimario
(P.S. If anyone want to continue solving Timus problem with me starting from 1077 and going down by difficulty, send me a message :))











I guess user rsalesc has explained to me the solution, so I will present it here:
Find any DFS tree of the graph (say 1-2, 2-5, 5-8, 5-3, 3-4 in the graph above). Now, each of the other edges will make a cycle using only the tree edges and that edge. For each edge, we can make a cycle. And for each cycle, we need one of those other edges. Therefore, the answer is the total number of non-tree edges. We can find the cycles with DFS and backtracking.