1. Одежда (A Div-2)
В этой задаче ограничения позволяли просто перебрать все возможные тройки i, j, k (которых не больше, чем 1003 = 1000000), для каждой тройки проверить, все ли элементы тройки подходят друг к другу, и среди троек, в которых все элементы подходят друг к другу, найти тройку с минимальной суммой ai + aj + ak.
2. Сумма цифр (B Div-2)
Изначально в числе не больше, чем 100000 цифр. Значит, после первого применения заклинания сумма цифр будет не больше, чем 9· 100000 = 900000, ее можно сосчитать простым проходом по строке из ввода. Значит, в нем будет не больше 6 цифр. После второго применения заклинания число станет не больше, чем 9· 6 = 54. То есть, число будет не более, чем двухзначным. Сумма цифр двузначного числа не больше 18, а сумма цифр числа, которое не больше 18, уже однозначна. Значит, Геральд сможет применить заклинание не больше 4 раз. При этом, чтобы первый раз посчитать сумму цифр нам понадобится 100000 сложений, а остальные действия незначительны.
3. Домашнее задание (C Div-2, A Div-1)
Для каждой буквы найдем количество раз, которое она встречается. Пусть 'a' встречается ka раз, 'b' встречается kb раз, и так далее. Наша задача --- выкинуть все вхождения как можно большего количества букв. Пусть мы выкинули какие-то x букв. Заметим, что если вместо этого выкинуть x самых редких букв, суммарное число выкинутых букв будет не больше. Значит, для любого числа x легко выяснить, можно ли удалить все вхождения каких-нибудь x букв. Соответственно, можно выбрать минимаьное такое x, для которого можно.
4. Автобусы (D Div-2, B Div-1)
Давайте для каждой остановки x от 0 до n посчитаем величину kx - количество способов на нее приехать. Рассмотрим i-тый автобус. Количество способов приехать на остановку ti на i автобусе, очевидно, просто равно количеству способов сесть в этот автобус. А сесть в этот автобус можно на остановке si, si + 1, ..., ti - 1. Таким образом, количество способов приехать на остановку ti на i автобусе равно сумме ksi + ksi + 1 + ... + kti - 1. Осталось заметить, что, чтобы найти общее количество способов попасть на остановку ti, надо просуммировать количества способов попасть на нее на каждом автобусе, у которого это конечная остановка.
Осталось решить две проблемы. Проблема первая: 0 ≤ n ≤ 109, поэтому все kx в память не влезут. Но, очевидно, нам понадобятся только остановки с ненулевым kx. Например, можно сжать координаты: создать список из всех встречающихся в условии остановок (а так же остановок 0 и n), отсортировать его, убрать повторяющиеся и заменить каждый номер остановки на его индекс в этом массиве. Тогда получится, что все остановки имеют номера в пределах 200001. Массив такой длины уже спокойно влезает в память.
Второе, если сумму ksi + ksi + 1 + ... + kti - 1 считать циклом, решение будет работать за O(m2), что не влезает в TL. Эта проблема тоже легко решается: можно создать и обновлять одновременно с массивом k[] массив sum[], в котором будем сумму элементов k до некоторого момента: sum[i] = k[0] + k[1] + ...\ + k[i - 1]. Иными словами, sum[0] = 0, sum[i + 1] = sum[i] + k[i]. Тогда количество способов доехать до остановки ti на i автобусе будет равно sum[ti] - sum[si].
Итого, сложность решения, O(m*log(m)) времени (за счёт сжатия координат), O(m) памяти.
5. Вектора (E Div-2, C Div-1)
Переформулируем задачу в комплексных числах.
Рассмотрим комплексные числа a = xA + iyA, b = xB + iyB и c = xC + iyC. С числом A разрешается делать операции A → A + C и A → iA.
Посмотрим, что может получится из числа A при применении к нему этих операций. Поскольку i4 = 1, то полученное число имеет вид A· ik + aC + biC - cC - idC для каких-то целых неотрицательных k, a, b, c, d, или, иными словами, A· ik + aC + biC для k = 0, 1, 2, 3 и целых a, b. Поскольку k может быть равно только 0, 1, 2 или 3, достаточно узнать, можно ли представить одно из чисел B - A, B - iA, B + A или B + iA в виде aC + biC.
Осталось научиться понимать, представляется ли некоторое комплексное число D в виде aC + biC. Запишем в виде системы линейных уравнений:
a· xC - b· yC = xD
a· yC + b· xC = yD
Решить систему линейных уравнений - это уже стандартная техническая задача.
6. Замок (D Div-1)
Перенумеруем вершины так, чтобы стартовая вершина, в которой исходно находится Геральд, получила номер 0.
Подвесим дерево, о котором идет речь в задаче, за вершину 0, и рассмотрим прямых потомков этой вершины. Пусть Геральд начал свой путь, пойдя в одну из этих вершин - вершину x. Далее после этого он должен обойти все поддерево этой вершины и вернуться в нее - иначе его маршрут пройдет не по всем вершинами. Далее он вернется из вершины x в вершину 0 и больше никогда не вернется в эту вершину. Далее он пойдет еще в какого-то предка вершины 0 (если, конечно, они у нее еще есть), и обойдет поддерево, подвешенное на эту вершину; и так далее. Пусть мы посчитали искомую величину для аналогичных задач на поддеревьях. Попробуем исходя из этого посчитать искомую величину для всего дерева. Это даст нам возможность решать задачу динамикой по поддереву.
Пусть у вершины 0 n сыновей. Пусть в них k1, k2, ..., kn потомков (включая них самих).
Пусть всего в дереве N вершин.
Пусть Ti - это удвоенная сумма длин всех ребер в i-том поддереве, включая ребро, ведущее в вершину 0. Это величина - ровно то время, которое потребуется Геральду, чтобы обойти все поддерево, начиная из вершины 0 и вернуться в вершину 0.
Наконец, пусть ti - ответ для подзадачи в i-той поддереве. Сразу прибавим к этому времени длину ребра между вершиной 0 и ее i-тым предком. Таким образом, это будет среднее время для поддерева с учётом того, что надо ещё дойти до него от вершины 0.
Пусть мы обошли поддеревья в порядке 1, 2, ..., n. Каково среднее время нахождения клада?
С вероятностью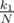 
клад окажется в первом поддереве. Тогда среднее время нахождения клада будет t1.
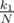клад окажется в первом поддереве. Тогда среднее время нахождения клада будет t1.С вероятностью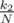 
клад окажется во втором поддереве. Тогда среднее время нахождения клада будет T1 + t2.
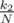клад окажется во втором поддереве. Тогда среднее время нахождения клада будет T1 + t2.И так далее. Таким образом, среднее время нахождения клада будет
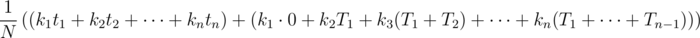
Посмотрим, можно ли улучшить это время? Поменяем местами поддеревья номер i и i + 1. Тогда из суммы исчезнет слагаемое ki + 1Ti и появится слагаемое kiTi + 1. То есть, сумма изменится на kiTi + 1 - ki + 1Ti. Сумма уменьшится, если это изменение меньше 0, то есть, если kiTi + 1 - ki + 1Ti < 0, что равносильно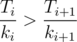 
.
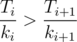.Таким образом, среднее время нахождения клада уменьшить не удастся, если поддеревья отсортированы в порядке возрастания величины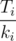 
, иначе найдется пара соседних поддеревьев, замена местами которых приведёт к улучшению результата. Таким образом, надо отсортировать поддеревья по этой величине, и обходить их этом порядке.
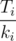, иначе найдется пара соседних поддеревьев, замена местами которых приведёт к улучшению результата. Таким образом, надо отсортировать поддеревья по этой величине, и обходить их этом порядке.7. Конфеты и Камни. (E Div-1)
Суть задачи в том, что есть доска n × m, на которой расставлены числа. И надо пройти от клетки (0, 0) до клетки (n - 1, m - 1), делая шаги на одну клетку вверх или вправо (то есть, увеличивая на 1 одну из координат) так, чтобы сумма чисел на клетках пути была максимальна.
Наша задача определить n + m - 1 клетку оптимального пути. Давайте начнем с малого: определим одну клетку этого пути, а именно среднюю. Пусть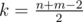 
. Какие клетки поля могут быть k-тыми? Очевидно, те, у которых сумма координат равна k, то есть, это будет диагональ прямоугольника. Поэтому очевидно, что несложно динамикой за O(nm) в нижнем треугольнике под этой диагональю посчитать, какое какую максимальную сумму можно набрать, придя в каждую из клеток этой диагонали. Аналогичной динамикой в верхнем треугольнике (на это раз сверху вниз) для каждой клетки на этой диагонали посчитаем, какую максимальную сумму можно собрать, стартовав с этой клетки. Сложив эти две величины, получим, какую максимальную сумму можно получить, пройдя через эту клетку. Осталось найти клетку (x, y), в которой достигается максимум. Её мы и возьмем за k-тую клетку нашего пути. Заметим, что в течение этой итерации мы использовали O((n + m)2) времени и O(n + m) памяти.
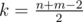. Какие клетки поля могут быть k-тыми? Очевидно, те, у которых сумма координат равна k, то есть, это будет диагональ прямоугольника. Поэтому очевидно, что несложно динамикой за O(nm) в нижнем треугольнике под этой диагональю посчитать, какое какую максимальную сумму можно набрать, придя в каждую из клеток этой диагонали. Аналогичной динамикой в верхнем треугольнике (на это раз сверху вниз) для каждой клетки на этой диагонали посчитаем, какую максимальную сумму можно собрать, стартовав с этой клетки. Сложив эти две величины, получим, какую максимальную сумму можно получить, пройдя через эту клетку. Осталось найти клетку (x, y), в которой достигается максимум. Её мы и возьмем за k-тую клетку нашего пути. Заметим, что в течение этой итерации мы использовали O((n + m)2) времени и O(n + m) памяти.Теперь рекурсивно перейдем к подзадачам, то есть, будем искать оптимальный путь от клетки (0, 0) до клетки (x, y), и от клетки (x, y) до клетки (n, m).
Осталось убедиться, что такое решение решение занимает ((n + m)2) времени.
Обозначим n + m за r.
На первом уровне рекурсии мы потратим r2 времени. На втором - два раза по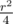 
. На третьем - 4 раза по 
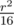, и так далее. Все будет потрачено времени 
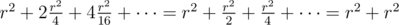. Таким образом, описанное решение занимает O((n + m)2) времени и очевидно, что оно занимает O(n + m) памяти.
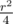. На третьем - 4 раза по 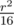, и так далее. Все будет потрачено времени 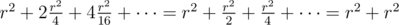. Таким образом, описанное решение занимает O((n + m)2) времени и очевидно, что оно занимает O(n + m) памяти.
Действительно, вы очень хорошо поработали - классный набор задач и качественный понятный разбор. Спасибо за это.
С нетерпением жду разбора задач D и E.
D:
Как считается обьём использованой памяти на якыках MS C++ и GNU C++ ?
Просто у меня один и тот же код на MS C++ АС, с ML=~20 Мб...а на GNU C++---чистый МL(
Или в чём ещё может быть проблема ?
В данном случае (видимо) s[t] - s[f] >= -mod, посему достаточно прибавить mod один раз.
>> достаточно прибавить некоторое количество раз mod
Тогда лучше (a%m+m)%m
res = (a - b + m) % m;
работает корректно и быстро (одно взятие по модулю вместо двух).
Ещё быстрее будет так:
res = a - b;
if (res < 0) res += m;
I think you are right.^_^
so the space is still
O(nm), but you split it in half (or a quarter), so that it takes25MB, and then compute the rest? Feels like the recursive solution, but you split it only once or so and the dp is simpler (its not a diagonal row). I'm not sure if i get your idea.I came up with a very similar solution. First I find all the cells of the middle diagonal and then use DP to find the cell inside the diagonal that also belongs to the optimal path. Then using DP and a bitset<200000000> I find the optimal path from the upper left corner to the cell in the diagonal (this is the first half). I do the same thing to find the optimal path from the cell in the diagonal to the lower right corner (this is the second half). I join both halves and the full path is totally recovered. Here is my submission: http://mirror.codeforces.com/contest/101/submission/31324561
tkae should be take
tkae should be take.
I think this is the Smallest Solution for the B problem
Nice solution... a little way to make it faster is by adding ths line before for loop :-
s.erase(remove(s.begin(),s.end(),'0'), s.end());
This helps in removing the unwanted '0' from the string which dosent add to change the sum
what is the use of subtracting v from the lower_bound iterato vector<pair<int,int> v ; int l = lower_bound(v, v + i, pii(v[i].second, 0)) — v;
I keep running into problems where I hit a wall because the input is too big for what I know how to handle in Java.
Question B is one of those problems. I am using longs and they still aren't long enough for the digits in the input.
Is this a sign that the answer has to be found with another language or is there a technique I don't know about?
Try using strings instead :)
I am not getting problem D.
I am not getting problem D.
Im also finding the solution very difficult to understand
Here is how I solved:
Let dp[x] be the number of ways to get to stop x. dp[0] = 1. So, for every bus i, you can do: $$$dp[t_i] = \sum_{s_i \leq j < t_i} dp[j]$$$. But we have a problem here, since $$$1 \leq t_i \leq 10^9$$$. You can use coordinate compression to handle this. You also can't compute this sum naively. I did it with a segment tree. Here is my submission for details.
i'm pretty sure that the time compelxity on problem E can be reduced to
O(nm)(which is less thanO((n+m)^2)whenn>>mor vice versa. The reasoning is that you splitnandmton/2andm/2respectively. In terms of the contest this is not required becausenandmhave the same upper bound of20'000. If the problem statement had said something in the terms ofn, m <= 1e5 but n*m <= 1e8, then this would be necessary.i'm pretty sure that for problem E, we can reduce the time complexity to
Θ(nm)which is less thanΘ(n+m)^2whenn>>mor vice verca. Because the constraints ofnandmare independent, its unnecessary. The problem statement could say"n,m <=1e5 but n*m<=1e6". The reasoning is that the diagonal dp row, can be wider (have a different ratio, not 1:1), which is weird to implement. This way, with the recursive calls we can divide independently the 2 dimensions (n/2, andm/2for the first division). Space compelxity is stillΘ(nm).242922518 my approach to the problem was to create a string consisting of integer characters, and adding the integer value of them to the variable called sum and after the summation is finished, converting the sum to the string and go on while the string.size() is bigger than 1 since the number we want is one digit.
sorry for my bad english, I hope this solution helps someone someday. Gl to all on their journeys.
I like the B problem easy implementation but i strugled to find the solution
can anyone provide the solution for Homework (C Div-2, A Div-1) i am a beginner to CP but this question looked interesting for greedy algorithm. i am having some difficulty in implementing it. Answer to this will help me a lot, Thanx:)