Can anybody suggest me optimal substructure for the above problem.
→ Pay attention
Before contest
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
18:58:02
Register now »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
18:58:02
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Find user
→ Recent actions
Write comment?
|
_jte_
|
13 years ago,
#
|
 0
0

Suggest that stuffing types are ordered from 0 to N (we also consider empty stuffing as a special kind of stuffing indexed zero).
Now, you can ask the question: What is the maximal amount of money you can earn if you have REST grams of dough and use stuffing types beginning from index INDEX to index N. Let F(rest, index) be the function that can answer this question. How can it be calculated? We can make count buns with IND stuffing where 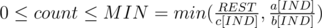 . . So, F(REST, IND) is equal to max{d[IND] * count + F(REST - c[IND] * count, IND + 1)}, where count = 0, ...MIN. F(REST, IND) = 0, if REST ≤ 0 or IND > N.
→
Reply
|
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/22/2024 22:36:59 (j2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










