Время-палиндром
Автор: Atef
В этой задаче необходимо найти следующий палиндром на цифровых часах. В задача точнось времени ограничивается минутами, и в сутках всего 24 * 60 минут. Соответственно, достаточно проверить все минуты, начиная с введённого времени, до тех пор, пока не будет обнаружен палиндром. Если палиндром не был обнаружен до конца дня, 23: 59, ответом будет 00: 00.
Типы данных
Автор: Atef
Будем считать пару типов данных (a, b), где a < b, "плохой" тогда и только тогда, когда существует числоx такое что x помещается в a бит, но x * x не помещается в b бит. Для решения задачи поможет следующее наблюдение. Лучшим кандидатом на число x будет максимальное число, которое помещается в a bits --- то есть x = 2a - 1. Таким образом, для каждого ai достаточно проверить что минимальное из aj > ai содержит достаточно бит, чтобы хранить x * x = (2a - 1) * (2a - 1), для которого требуется максимум 2 * a бит. Для того, чтобы находить следующее минимальное aj > ai числа на входе имеет смысл предварительно отсортировать.
Водоснабжение
Автор: Atef
В задача задаётся граф корпусов общежития и направленных труб между ними. По условию задачи этот граф будет содержать одну или блее цепочек труб. Необходимо найти начало и конец каждой цепочки, принимая во внимания, что цепочка может состоять из более чем одной трубы.
Также для каждой цепочки необходимо найти наиболее слабое звено. Чтобы сделать это, следует пройти по каждой цепочке, например, запуская поиск в глубину из каждого корпуса не имеющего входящих труб. Эти корпуса будут началами цепочек, и, по ходу поиска в глубину, нужно также помнить минимальный диаметр среди встреченных труб. После того, как все цепочки найдены, перед выводом их следует отсортировать по номеру корпуса, откуда выходит данная цепочка.
Автор: Atef
Рассмотрим два множества возможных команд: команды, где Мистер Вафа является единственным студентом со своего факультета и команты, где хотя бы один студент с факультета Мистера Вафы, кроме самого Мистера Вафы, является членом команды. Эти множества не пересекаются. Если вычислить количество команд в первом множестве --- A, и количество команд во втором множестве --- B, то ответм будет B / (A + B).
Количество команд в первом множестве A = 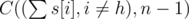 . Нужно вычесть единицу так как Мистер Вафа точно является членом команды, а оставшиеся (n - 1) игроков будут выбраны из оставшихся
. Нужно вычесть единицу так как Мистер Вафа точно является членом команды, а оставшиеся (n - 1) игроков будут выбраны из оставшихся 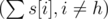 студентов.
студентов.
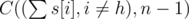 . Нужно вычесть единицу так как Мистер Вафа точно является членом команды, а оставшиеся (n - 1) игроков будут выбраны из оставшихся
. Нужно вычесть единицу так как Мистер Вафа точно является членом команды, а оставшиеся (n - 1) игроков будут выбраны из оставшихся 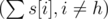 студентов.
студентов.Теперь найдем количество команд, где кроме Мистера Вафы в команде есть ещё k студентов с его факультета. Это будет 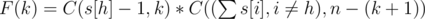 . По аналогии с количеством команд в первом множестве, нужно выбрать (n - (k + 1)) студентов с других факультетов и ни один из них не должен быть с факультета Мистера Вафы. Таким образом, общее количество команд, где у Мистера Вафы будет хотя бы один партнёр по команде с его факультета, равно
. По аналогии с количеством команд в первом множестве, нужно выбрать (n - (k + 1)) студентов с других факультетов и ни один из них не должен быть с факультета Мистера Вафы. Таким образом, общее количество команд, где у Мистера Вафы будет хотя бы один партнёр по команде с его факультета, равно 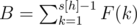 .
.
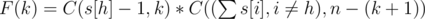 . По аналогии с количеством команд в первом множестве, нужно выбрать (n - (k + 1)) студентов с других факультетов и ни один из них не должен быть с факультета Мистера Вафы. Таким образом, общее количество команд, где у Мистера Вафы будет хотя бы один партнёр по команде с его факультета, равно
. По аналогии с количеством команд в первом множестве, нужно выбрать (n - (k + 1)) студентов с других факультетов и ни один из них не должен быть с факультета Мистера Вафы. Таким образом, общее количество команд, где у Мистера Вафы будет хотя бы один партнёр по команде с его факультета, равно 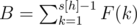 .
.Выше приведено математическое решение. Оно допускает множество алгоритмических реализаций.
Автор: Atef
С первого взгляда ограничение на n в 1018 кажется огромным. Однако, в сочетании с тем, что ответ следует вывести по модулю 12345 оно должно не пугать вас, а наоборот, помогать думать в правильном направлении: как решить задачу методом динамического программирования.
Как и во всех задачах на динамическое программирование, подход заключается в том, чтобы разбить задачу на подзадачи и понять, какую дополнительную информацию следует передавать из поздадачи в подзадачу чтобы в итоге добраться до решения общей задачи.
Предположим, что n равно 11, и у нас есть решение для первых 10 преступлений. Понятно. что просто знать ответ --- количество способов, которыми можно совершить первые 10 преступлений и остаться безнаказанным --- недостаточно для того, чтобы решить задачу для n = 11. Дополнительной информацией, которую необходимо передать из подзадачи в подзадачу является следующее множество чисел: количества способов, которыми можно совершить первые n преступлений, имея после этого кратности преступлений по всем типам d1, d2, ...d26 соответственно. Так как произведение кратностей во входном файле не превосходит 123 размер множества всех возможных комбинаций кратностей тоже ограничен сверху ста двадцатью тремя.
Чтобы лучше понять эту идею, рассмотрим первый тест из условия. В нём есть два ограничения, A с кратностью 1 и B с кратностью 2. Остаток по преступлениям типа A всегда ноль. Остаток по преступлениям типа B может быть либо нулём либо единицей. Таким образом, решая подзадачу для первых n2 < = n преступлений, достаточно помнить два числа: "количество способов, которыми можно совершить n2 преступлений и быть невиновным по всем статьям", и "количество способов, которыми можно совершить n2 преступлений из которых есть одно ' нескомпенсированное' преступление типа B".
Ключевым шагом к решению теперь является наблюдение, что каждый переход от моножества решений для первых k преступлений ко множеству решений для первых (k + 1) преступлений можно задать матрицей перехода. Эта матрица будет одинаковой на каждом шагу. После построения этой матрицы задача можеть быть решена за логарифм от n = 1018 используя идею matrix exponentiation: на некоторых шагах вместо того, чтобы вычислять Ai + 1 = Ai· A0 можо вычислить A2i = Ai· Ai.
до
Последним подводным камнем в этой задача являются множественные кратности. Если бы у каждого преступления была максимум одна кратность, достаточно было бы хранить в множестве состояний текущую кратность по данному преступлению. Более того, после возведения матрицы в степень единственным допустимым состояниям было бы состояние, где все кратности равны нулю.
Если же множественные кратности разрешены, то для каждого типа преступлений нужно хранить кратности по могулю произведения всех допустимых кратностей для этого типа претуплений. (Строго говоря, достаточно хранить кратности до наименьшего общего кратного кратностей, но в данных огранчениях это не требуется.) Затем, на этапе вывода ответа, вместо того, чтобы вывести содержимое одной клетки финальной матрицы, следует пройтись по всем её элементам и выбрать те, красности по которым удовлетворяют входным ограничениям на кратности.
Размещение
Автор: Atef
В задаче требуется найти лексикографически n-ю сортировку, удовлетворяющую данным ограничениям.
Подвох, который смутим многих участников, а заодно и некоторых тестеров и авторов опорных решений, заключается в том, что вместо интуитивного ограничения в формате position[a[i]] < position[b[i]] ограничения в этой задача имеют вид element at position[a[i]] < element at position[b[i]].
В большинстве задач, где следует вывести лексикографически n-ое решение, хорошей идеей, зачастую приводящей к решению, является идея научиться считать количество возможных решений, на которые ракладываются некоторые ограничения.
Перед тем как научиться считать количество возможных решений, давайте поймём как это поможет нас решить задачу. Для начала сделаем следующее наюлюдение: если общее количество решений меньше, чем y - 2000, то ответом будет "The times have changed". А когда эта проверка на существование решения произведена, найти само решение можно, например, подбирая его слева направо.
Подобрать решение можно, наример, так: зафиксируем первый элемент равным единице и подсчитаем количество возможных решений. Если их меньше, чем индекс перестановки, которую нужно найти, то первым элементов результирующей перестановки должна быть единица --- поскольку все перестановки, где первым числом идет единица лексикографически меньше перестановок, где первый элемент больше единицы, и, таким образом, если мы допускаем гипотезу, что первый элемент может быть не единицей, мы сразу приходим к противоречию.
А если зафиксировать первый элемент в единицу не дало нам достаточно перестановок, тогда следует уменьшить y на количество перестановок, где первым элементом является единица, и продолжить поиск в предположении, что первым элементов является двойка. Вычесть количество перестаноков, где первым эдементов является единица, необходим, потому что, согласно условию задачи. мы пропускаем те порядки размещения, которые использовались в 2001, 2002 и т.д. годах.
Процеесс подбора следует продложать пока все элементы не были зафиксированы на каких-то значаниях. Когда первый элемент перестановки становится известным, можно приступать ко второму элементу, затем к третьему и т.д.
Теперь, чтобы решение стало полным, нужно уметь вычислять количество перестановок, удовлетворяющих двум ограничениям: набору ограничений на граф размещения из теста и зафиксированному префиксу. Эта часть задачи решается динамикой.
Для данного префикса P необходимо подсчитать количество способов, которыми можно разместить оставшиеся (n-m) элементов не нарушив ни одного ограничения.
Предположим, что мы будем генерировать все возможные перестановки. Однако, вместо стандартного подхода "попробуем поставить на позицию i любой свободный элемент и решим задачу для оставшихся позиций начиная с (i+1)-й", используем несколько иной подход: "для данного способа разместить первые i элементов, не считая элементов, которые образуют префикс, возьмём (i+1)-й элемент и проверим все позиции, куда его можно было бы поместить". При этом будем идти по элементам в возрастающем порядке, пропуская, конечно, элементы, которые являются частью уже известного префикса.
Несложно видеть, что такой алгоритм генерации всех перестановок работает, но за время O((n - m)!), что конечно, недопустимо. Соответственно, нужно каким-то образом уменьшить пространство состояний, чтобы свернуть этот алгоритм генерации перестановок в динамику.
Необходимое нам наблюдение такое: состояние частично решённой задачи однозначно задаётся битовой маской использованых позиций. С первого взгляда может показаться, что этой информации недостаточно, так как на будущие ограничения влияет не только маска занятых позиций, но и то, в каком порядке расположены элементы на этих позициях. Однако, это оказывается несущественным, если заполнение перестановки элементами производится в порядке возрастания свободных элементов. Действительно, пусть для некоторой маски занятых позиций мы хотим поставить элемент e в свободную позицию i. Чтобы проверить допустимо ли такое положение для элемента e, будем проверять те пары входных ограничений, которые касаются позиции i. Если ограничение касается позиции i и другой позиции, которая ещё свободна, то оно не нарушается элементом e. Если же ограничение накладывается на позицию e и другую позицию, в которой уже есть элемент, то верно одно из двух: либо другая позиция принадлежит префиксу, и тогда мы точно знаем, какой на ней стоит элемент, либо же нам заведомо известно, что элемент на этой позиции меньше, чем e, потому как наша динамика расставляет элементы начиная с меньших.
Дартс
Автор: Dima
Перед тем, как перейти к алгоритму, отметим, что ответом на задачу будет отношение суммарной площади всех прямоугольников к площади объединения всех прямоугольников.
Чтобы понять это, сделаем следующее наблюдение. В первую очередь понятно, что если все прямоугольники совпадают, то ответом будет их количество. Теперь временно забудем про то, что фигуры должны быть прямоугольниками, предположим, что форма фигур на входе может быть любой, и покажем как построить пример, где площать объединения была бы s и ожидаемое среднее количество проткнутых фигур было бы e. Понятно, что такой пример можно построить начав с произвольного контура объединения, ограничевающего площать s, путём добавления дополнительных фигур, лежащих внутри этого контура. Суммарно необходимо будет добавить фигур на общую площать t = s· (e - 1), но конкретное число не важно. Важно то, что взаимное расположение этих добавленных фигур не имеет значения, и, соответственно, ответ на исходную задачу зависит только от площади контура объединения всех фигур и суммарной площади всех фигур.
Вернёмся теперь к прямоугольникам. Найти суммарную площадь всех прямоугольников легко. Сложно найти площадь объединения всех прямоугольников быстрее, чем за O(n3). Обратите внимание, что объединение может состоять из множества несвязных компонент, компоненты не обязаны быть выпуклыми, они могут содержать дырки, и вообще, в общем случае описать объединение всех входных прямоугольников не очень просто. К счастью, в этой задаче нас интересует только площать этого объединения.
Одно из решений, которое относительно несложно закодировать, заключается в следующем. Будем считать площадь объединения методом трапеций. Отметим сразу, что для вычисления площади методом трапеций достаточно знать все ориентированные сегменты контура, а их порядок совершенно не важен. Таким образом достаточно "просто" найти все ориентированные сегменты, которые образуют контур объединения, причём вертикальные сегменты могут быть сразу исключены из рассмотрения.
Например, если для какого-то теста объединение представляет собой фигуру с дыркой, то внешний контур должен превратиться во множество сегментов с положительной общей площадью, а внутренний контур --- во множество сегментов с отрицательной общей площадью. Иными словами, внешний контур следует обойти по часовой стрелке, а внутренний --- против часовой стрелки.
Для того, чтобы найти все такие сегменты, рассмотрим все различные невертикальные прямые, на которых лежат стороны входных квадратов. Их не больше, чем 4n. Понятно, что каждый сегмент объединения лежит на одной из этих прямых, соответственно, достаточно проверить отдельно каждую из прямых, но только по одному разу.
Правила, по которым можно выделить "положительные" и "отрицательные" сегменты на каждой прямой достаточно просты:
1) Если сегмент этой прямой (x1, y1) - (x2, y2) является частью границы одного из входных прямоугольников, тогда помечаем этот сегмент как "положительный" или "отрицательный" в зависимости от того, лежит ли данный прямоугольник выше или ниже прямой.
2) Если на сегменте этой прямой (x1, y1) - (x2, y2) накладываются границы двух входных прямоугольников, лежащих по разные стороны от прямой, то этот сегмент не може являться частью контура.
3) Если сегмент (x1, y1) - (x2, y2) лежит полностью внутри какого-то из входных прямоугольников, то он не может являться частью контура.
Соответственно, построить все сегмента контура объединения можно с помощью примерно следующего кода:
для каждой уникальной не-вертикальной прямой
создаём массив маркеров. маркер хранит x-координату и одно из четырёх событий: { начало/конец положительного сегмента, начало/конец отрицательного сегмента }
проходим во всем входным прямоугольникам
если одна из сторон этого прямоугольника принадлежит рассматриваемой прямой
добавляем два маркера: начало и конец сегмента. знак сегмента определяется положением прямоугольника относительно рассматриваемой прямой.
иначе если это прямоугольник пересекается с прямой
находим левую и правую точки пересечения, и помечаем сегмент между ними четырьмя маркерами, покрывая его и положительным и отрицательным сегментом.
сортируем массив маркеров по их x-координате
идём по маркерам слева направо. если про какой-то сегмент известно, что он должен быть положительным, и не должен быть отрицательным, выводим его как положительный сегмент финального контура. если известно, что он должен быть отрицательным и не должен быть положительным, выводим его как отрицательный сегмент финального контура.
После этого можно было бы выписать множество финальных контуров используя, например, поиск в глубину, но для метода трапеций это не требуется. Достаточно просуммировать (x2 - x1)· (y1 + y2) / 2 для каждого сегмента.
Вышеописанное решение работает за O(n2· logn) : для каждой из O(n) прямых мы рассматриваем O(n) пересечений, и их сортировка занимает O(n· logn) на каждую прямую.











We can just check (MN - minutes in input, HR - hours in input):
This is a statement of your problem B. Here you use a word some which change the meaning of the statement what you want to mean. This statement mean if there are any aj which fullfil the condition ai < aj, tutuf will continue using Gava. The word some totally change the statement here and I got wrong over and over only for that reason. Is not it a mistake?
then plz help me the 4th test case at which my code failed
I used the following idea: let x = all possible teams=
I used the following idea: let x=all possible teams=
Is anything wrong in the reasoning? I got stuck on test 21. submission[635824]. Code is here.
A = C ( sum(s[i] i!=h) - 1, n - 1), I think it should be A = C ( sum[i] i!= h), n - 1). Why we must subtract 1 ?
And F(k) = ... sum(s[i] i!=h) - (k + 1), why we must subtract (k + 1) ?
F(k) = C( s[h] - 1, k) * C( sum(s[i] i!=h), n - (k + 1) )
В английской версии разобрана.(I always can't get acorss the editorial >_< ) ...
Can someone explain how to calculate the transition matrix for Div1 D(Crime Management),and also what should the dp state be?
Thanks. good editorial