1. Lucky Number (Div2 A)
В этой задачи нужно просто пройтись по цифрам числа и посчитать количество счастливых. Если оно ровно 4 или 7 (44 и больше, естесвенно, быть не может) то выводить YES, иначе NO.
2. Lucky String (Div2 B)
Нужно заметить, что результат - это префикс длины n строки abcdabcdabcd...abcd и вывести его.
3. Lucky Sum of Digits (Div1 A, Div2 C)
Пусть в результате a цифр 4 и b цифр 7. Естественно, что a * 4 + b * 7 = n. Переберем b. Зная b можно найти a, 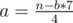 . Среди всех пар (a;b) нам нужно выбрать такую, что a + b минимально, среди таких пар выбрать ту, что b минимально и вывести число вида 44...4477....77, тут количество четверок равно a, количество семерок - b.
. Среди всех пар (a;b) нам нужно выбрать такую, что a + b минимально, среди таких пар выбрать ту, что b минимально и вывести число вида 44...4477....77, тут количество четверок равно a, количество семерок - b.
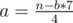 . Среди всех пар (a;b) нам нужно выбрать такую, что a + b минимально, среди таких пар выбрать ту, что b минимально и вывести число вида 44...4477....77, тут количество четверок равно a, количество семерок - b.
. Среди всех пар (a;b) нам нужно выбрать такую, что a + b минимально, среди таких пар выбрать ту, что b минимально и вывести число вида 44...4477....77, тут количество четверок равно a, количество семерок - b.4. Lucky Probability (Div1 B, Div2 D)
Пусть L[i] - i-е счастливое число, нумерация с 1 (L[0] = 0, L[1] = 4, L[2] = 7...). Переберем сначала первые k счастливых чисел, затем вторые k и т. д. Для каждой такой группы найдем вероятность, результат будет суммой этих чисел. Пусть индекс первого счастливого числа i, последнего j (j = i + k - 1). Тогда нам надо найти пересечение промежутков [pl;pr] и (L[i - 1];L[i]], а также [vl;vr] и [L[j];L[j + 1]), произведение этих чисел и будет количество способов таких, что p < v, аналогично делаем для p > v. Сумма всех этих способов для каждого i и будет общим количеством способов, вероятность = количество способов / ((pr - pl + 1) * (vr - vl + 1)).
5. Lucky Tree (Div1 C, Div2 E)
Решим задачу используя метод динамического программирования. Подвесим дерево за какую-то вершину, например 1. Пусть F(x) - количество вершин в поддереве x таких, что на пути из x в эту вершину есть как минимум одно счастливое ребро. Считать F(x) будем рекурсивно. Если x - листок дерева, то F(x) = 0. Иначе, если от x выходит счастливое ребро в y, то к F(x) нужно додать C(y), иначе F(y) (Здесь C(x) - количество вершин в поддереве x, включая вершину x). Но для решения этой задачи, нам нужно еще знать для каждой вершини количество вершин вне поддерева, на пути до которых есть счастливое ребро. Назовем это количество F'(x). Для корня дерева F' ровно 0. Будем идти рекурсивно из вершины-корня, при этом если мы рассматриваем какую-то вершину, то F' для нее уже посчитан. Пусть сейчас мы в вершине x и хотим перейти в вершину y. Если ребро между этими вершинами счастливое, то F'(y) = C(0) - C(y), иначе F'(y) = F'(x) + F(v) - F(to) (действительно, если ребро не счастливое, то нам к результату для x нужно еще додать сумму F(i) для всех i которые есть синовями x и i ≠ y).
После этого результатом будет 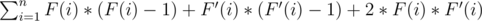
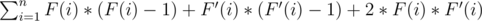
6. Lucky Sorting (Div1 D)
Прежде всего проверим, посортированая ли входная последовательность. Если так, просто выведем 0. Иначе, если в массиве нет счастливого числа, то выведем - 1. Иначе, отсортируем массив (пусть входной массив називается A, отсортированый - B). Тепер для каждого елемента из A у нас есть его позиция в B. Пусть минимальное счастливое число имеет индекс k. Пусть нам нужно поставить елемент из индексом i на позицию j. Чтобы это сделать, нужно сначала чтобы элемент в позиции j был счастливым числом. Если это не так, то сделаем Swap(A[k], A[j]), после этого Swap(A[i], A[j]). То есть, что-бы вставить какой-то елемент массива на нужное место нужно не больше чем две операции. Для всех обменов найлучше использовать минимальное счастливое, при этом его самого не обробатывать (после обробки всех кроме него, очевидно, он тоже будет на своем месте). Также в этой задачи нужно аккуранто поддерживать индексы всех елементов.
7. Lucky Interval (Div1 E)
Это лишь один вариант решения, возможны различные модификации. Но, надеюсь, эти размышления натолкнут Вас на решение.
При ограничениях a и b до 107 задача решается используя КМП: рассмотрим строку следуещего вида: F(1)F(2)F(3)F(4)...F(3 * 107). Нужно найти первое вхождение после индекса a строки F(a)F(a + 1)F(a + 2)...F(a + l - 1). Сложность такого решения O(a + l), естественно что такое не проходит по времени и памяти. Попробуем оптимизировать этот алгоритм используя несколько фактов из "Теории счастливых чисел".
Разобьем все числа на блоки по 100, то есть первый блок - [0;99], второй - [100;199] и т. д. Введем понятие класса блока. Номер класса блока ровен F(i / 100), где i - какое-то число из этого блока. Различных классов блоков будет ровно 8. Подряд-идущих блоков с одинаковыми номерами классов будет максимум 6. Все это можно увидет используя перебор.
Утверждение #1: если l ≥ 1000, то 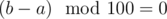 .
.
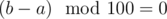 .
.Доказательство: рассмотрим строку F(100 * k)F(100 * k + 1)...F(100 * k + 99). Таких различных строк буде столько само, сколько различных классов. Например, для первого класса она будет иметь вид:
0000100100000010010000001001000000100100111121121100001001000000100100111121121100001001000000100100
для второго:
1111211211111121121111112112111111211211222232232211112112111111211211222232232211112112111111211211
и т.д. По структуре этих строк видно, что блоки различних классов не могут пересекаться (то есть при любом пересечениее освпадения не будет), отсюда следует, что любая последовательность подряд идущих блоков в которой есть хотя-бы два блоки с различными классами будет совпадать только с такой самой последовательностью, то есть смещение будет кратное 100. Так как подояд-идущих блоков с одинаковимы классами будет не больше 6, то при l ≥ 1000, очевидно, будут различные блоки, что и требовалось доказать.
Поэтому, задачу с l ≥ 1000 можно решить используя алгоритм КМП со сложностью O((a + l) / C), где C равно 100, пусть функция которая будет это делать называется Solve(l, r).
Тепер нужно научиться решать задачу с l < 1000. Сначала заменим a на минимальное a' такое, что F(a') = F(a), F(a' + 1) = F(a + 1), ..., F(a' + l - 1) = F(a + l - 1), a' / 100 = a / 100, это можно сделать простым перебором. Тогда результат будет минимум из следующих чисел:
- r = Solve(a', a' + l - 1);
- Минимального r', такого что r - r' < = 1000, r' > a, F(r') = F(a), F(r' + 1) = F(a + 1), ..., F(r' + l - 1) = F(a + l - 1).
- Минимального a'' такого, что a'' > a, a'' - a ≤ 1000 и F(a'') = F(a), F(a'' + 1) = F(a + 1), ..., F(a'' + l - 1) = F(a + l - 1).
Естественно это решает проблему возможного не кратного 100 смещения блоков, но есть и вариант, который ставит это под сомнение. Пусть входной промежуток только в блоке с номером класса C. Тогда, есть вероятность, что лучше пойти в блок с номером C + 1, например (397;1) → (400;1). На самом деле, второй пункт решает эту проблему, так как если и блок C + 1 будет перед блоком C (а только в том случаи будет выгоднее его взять), то эти два блоки будут соседними (здесь имеется ввиду блок с классом C, правее блока со входным промежутком). Доказать это можно следующим, довольно важным, утверджением (с помощью которого можна доказывать и другие моменты), подтвердить которое можно перебором:
Утверждение #2: если есть два соседних блока, то абсолютная разница номеров их классов не превысшает 1.
Отсюда следует, что если после блока C (в котором есть входной промежуток) идет блок C - 1, то до блока C мы доберемся перед C + 1, если до C или C + 1 то его и выберем.
Таким образом, задача решается просто аккуратным разбором всех моментов. Сложность решения: O((A + L) / 100), авторское решние работает 1.5 сек. и использует 250 мб. памяти.
Среди авторских решений было и такое, что разбивает на блоки размером в зависимости от l, которое работает намного быстрее.











Как уже было сказано в другой теме, div1-C можно намного проще (сам как раз писал авторскую динамику, не успел:( )
Если удалить из графа "счастливые" ребра, то между двумя вершинами начального графа нету пути через заданную вершину тогда и только тогда, когда они лежат с ней в одной компоненте звязности в полученном графе.
Дальше очевидное и значительно более короткое решение с СНМ или одной серией обходов в глубину (для разбиения на компоненты) и элементарной комбинаторикой.
Ответом будет сумма ответов для всех вершин, а ответ для каждой вершины равен (n-t[i])*(n-t[i]-1), где n - начальное число вершин, t[i] - число вершин в компоненте нового графа, которая содержит i-ую вершину.
For problem lucky tree. ..
I have found another algorithm within some participator's code ...
(... which is much easier to implement than above .. )
For each "lucky edge", maintains a group of component by Union-Find-Set.. .Igore each "lucky edge", maintains the residual graph by dsu。
Then you can get the result by some combinatorics method ..
Could anyone explain this thought further ? ..
Let's erase all lucky-weighted edges from the tree. Then, any two vertices are in different connected components if and only if the path between them in the original tree contained a lucky edge.
So it's sufficient to ignore lucky-weighted edges while reading the input, compute the connected components' sizes (using BFS, DFS or Union-Find), and then, for every vertex v, let's denote by f(v) the number of vertices in different connected components than v (unreachable from v). Let's count the triples beginning with v. Their number is f(v) * (f(v) - 1). We do this for all v (or alternatively for whole connected components at once) and return the sum.
Hope that this clarifies the approach. I think this solution is not only easier, but it also works for arbitrary connected graphs, not just trees (if we replace "the way" by "any way" in the problem statement).
。paulocezar && dj3500。。Thanks a lot 。!!。:)
Thanks Before :D
P.S : I'm using Java
The problem is you shouldn't build string then print it. it takse much time. particularly in java.
you must directly print characters.
something like this: for(int i=0 ; i<n ; i++) System.out.print((char)(i%4+'a'));
if i just thought twice before submitting I'd be in div.1 now.
The key is to notice that there not so many lucky numbers: 2046 in the range [1,10^9]
Now if there are k lucky integers between min(v,p) and max(v,p), they must be
consecutive: There is some i such that it's the set L[i] .. L[i+k-1].
Iterate over i, add the probability that min(v,p)<=L[i] and L[i+k-1] <= max(v,p).
There is a catch with k=1: the case where min(v,p) == L[i] == max(v,p) is
counted twice that way, so it has to be corrected.
For Lucky sum of Digits, is the second part of the statement necessary? As in, if we have two pairs (a1,b1) and (a2,b2) such that a1+b1 = a2+b2, then it has to be that a1 = a2 and b1 = b2. We don't need to check again amongst those pairs.
I solved Div1 A using an observation that there can't be more than 6 4s together. If there are, those 7 or more 4s can be replaced by 4 7s as 7 * 4 = 4 * 7, which obviously shall be a smaller number. Secondly, all 4s should be at the beginning so as to make the number as small as possible, Thus I counted the number of 7s till the number is less than or equal to 24 and divisible by 4. Incase it is never divisible by 4, I output -1. Else, I just add 4s and that's it. Code: https://mirror.codeforces.com/contest/109/submission/52615818
Thanks. good editorial