Родилась интересная идея в рамках "поделки на коленке", которой спешу поделиться.
Есть много алгоритмов факторизации (например, описанные на e-maxx), но, кажется, что всем им можно понаходить нехорошие контрпримеры в данном диапазоне (по крайней мере, они известные стандартные, и можно ждать подобного, хотя в детали не вдавался - может быть, просветят).
Пусть дано N ≤ 1018. Для начала, проверим маленькие делители до 107 (решето Эратосфена и деления должны уложиться в таком диапазоне). Также проверим, что число не точный квадрат.
Теперь, число либо простое, либо имеет два простых делителя не больше 1011. Попробуем найти функцию Эйлера от числа 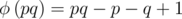 . Очевидно, что она лежит в диапазоне
. Очевидно, что она лежит в диапазоне 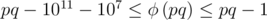
Зададимся некоторым a. Предпросчитаем an для n ≤ 107. Если у числа окажется маленький порядок, то просто запомним этот порядок. Иначе с шагом 107 пройдем диапазон значений pq - 1011 - 107 ≤ n ≤ pq - 1 + 107 и обнаружим решения an = 1, в которых одно из n будет являться искомым значением функции 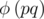 . Удостовериться, что данное значение является искомым можно просто решив квадратное уравнение и проверив один из получившихся делителей.
. Удостовериться, что данное значение является искомым можно просто решив квадратное уравнение и проверив один из получившихся делителей.
Будем проверять a начиная с двух и так далее. Единственной особенной ситуацией может быть то, что много чисел в начале будут иметь маленький порядок. Будем попутно считать НОК всех получившихся порядков, и, как только этот НОК будет больше 107 проведем процедуру проверки на 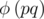 с шагом НОК.
с шагом НОК.
Не реализовывал, хотя выглядит верным. Discuss.
Upd 1. Сортировать 107 чисел после предпросчета может быть долго. Быть может, надо понизить эту константу до 106 (105 проверок нас вполне устроит). Кроме того, можно использовать тот факт, что 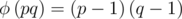 делится на 4 и наш шаг делится на 4 и сохранить только 107 / 4 шагов предпросчета.
делится на 4 и наш шаг делится на 4 и сохранить только 107 / 4 шагов предпросчета.
Upd 2. Итого к реализации: gcd, быстрое возведение в степень, решето Эратосфена, решение квадратного уравнения, точное извлечение корня из числа до 10^18. Не так много и совсем стандартно.











Я всегда проверяю до 10^6, а потом могут остаться максимум 2 простых числа, которые определяю Поллардом-ро. Пока работало.
Кстати, а зачем тут решето Эратосфена? Можно же просто проитерировать все числа от 2 до 10^6 и проверить, делится ли N на них.
Знаю про ро-эвристику, читал в Кормене, реализовывал. Кажется, на моей реализации были какие-то проблемы иногда, т.е. что можно таки ее заставить работать долго специальными тестами.
Решето, потому как мне жизненно важен каждый порядок в проверке маленьких простых (мне надо отсечь большое простое).
У поларда не нравится, в частности, рандомизация.
Если найдете свою реализацию - дайте пожалуйста, можно погонять.
http://en.wikipedia.org/wiki/Fermat's_factorization_method
Видимо, речь об этом. Придется писать заодно тест на простоту, ибо
> If N is prime (so that c = 1), one needs O(N) steps!
Вообще, это плохой знак. Вполне возможно, что и после теста на простоту если искомые делители различаются раз в 10, будет поломато. Проверю вечером.
http://ru.wikipedia.org/wiki/Метод_Лемана
Прочитал. Можно попробовать реализовать, хотя, боюсь, придется неплохо шаманить, в частности, нужна поддержка 128 бит (ручная?) при вычислении корня квадратного из 4*k*n.
Второй вопрос - получится ли уложить в нормальное время, поскольку придется делать в худшем случае 107 проверок >64-битного числа на точный квадрат.
Откуда 107?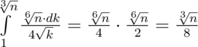 . Это где-то 2·105 и даже меньше. При том что это вроде оценка сверху.
. Это где-то 2·105 и даже меньше. При том что это вроде оценка сверху.
int b1 = sqrt3(n);
int cnt = 0;
for (int i=1;i<=b1;i++)
{
int b2 = (int)(pow(double(n), 1.0/6) / 4 / pow (double(i), 1.0/2) + 1);
for (int j=0;j<=b2;j++)
++cnt;
}
2102446
Ай! 2*10^6, лишний нолик в выдаче подкрался незаметно. Да, поменьше будет.
Да даже больше могут различаться. Собственно идея в том, что два простых, далёких друг от друга. Уже как-то тестировал, виснит только так.
пример 999999999809997023 = 56005919 * 17855255617.
Вспомнил, что не нравилось в ро-эвристике. Кажется, при неудачном начальном выборе будет зацикливание, и его надо аккуратно ловить.
Так что хочется Вашу реализацию.
> я даже не представляю как искать
> cкорее всего нет
Домашнее задание. Заставить HashSet<Integer> в Java работать более 2 секунд на сервере Codeforces при последовательном добавлении N = 50000 чисел, не превышающих 10^9