div2 A. В этой задаче нужно было найти длину ломаной, умножить ее на k / 50 и вывести что получилось. Длина ломанной --- сумма длин всех ее звеньев. Длина каждого звена считается по теореме Пифагора: .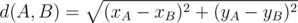

div2 B. Идею этой задачи подкинул RAD, поскольку это была последняя задача в комплекте, и мне уже ничего простого в голову не лезло:) Спасибо ему за это.

Посчитаем значения массива cnt[100], в котором будем хранить количество палочек соответствующей длины. Теперь посчитаем количество доступных пар палочек одинаковой длины. Оно равно 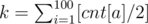, где [x] --- целая часть числа x. Для каждой рамки нужно 2 такие пары, причем можно выбирать любые из них. Поэтому ответ будет равен z = [k / 2].

div2 С. div1 A. Во первых, нужно отдельно обработать случаи, когда t₀ = t₁, t₀ = t₂ и t₁ = t₂. Ответы в этих случаях будут (x₁, 0), (0, x₂) и (x₁, x₂). Последние 2 случая в претестах отсутствовали.

Далее, для всех 1 ≤ y₁ ≤ x₁ нужно найти такое минимальное y₂, что t(y₁, y₂) ≥ t₀. Это можно было делать тремя способами: бинпоиском, двумя указателями или же просто вычислением по формуле [y₁(t₀ - t₁) / (t₂ - t₀)], где [x] --- округление числа x вверх. Перебрав все такие случаи, выбираем оптимальный.

Последний коварный случай состоит в том, что для всех 1 ≤ y₁ ≤ x₁ и 1 ≤ y₂ ≤ x₂ t(y₁, y₂) < t₀. Например, в тесте

100 110 2 2 109 (это 6ой претест).

В этом случае следует выводить (0, x₂).

Все вычисления должны быть выполнены в 64-битных числах (8ой претест был как раз на переполнение промежуточных вычислений) или же очень аккуратно в вещественных числах.

div2 D. div1 B. Посчитаем префикс-функцию для всей строки. Префикс-функция p[i] --- это длина наибольшего префикса, который также является суффиксом подстроки [1... i]. Подробнее о префикс-функции можно нагуглить, например, в описании алгоритма Кнута-Морриса-Пратта (КМП).

Первый кандидат в ответы --- префикс длины p[n]. Если p[n] = 0, то решения нет. Иначе пройдемся по всему массиву p и, если встретим где либо еще одно значение, равное p[n] --- то мы нашли ответ. В случае неудачи, второй кандидат на ответ --- префикс длины p[p[n]]. Если p[p[n]] = 0, то решения нет. Иначе сразу можно сказать, что ответ найден. Этот подстрока является и префиксом, и суффиксом, а так же суффиксом префикса длины p[n], который находится где-то внутри строки. Это решение работает за O(n).

Эту задачу можно было так-же решить и с помощью хэшей. Проверим все суффиксы на соответствие префиксам --- получим некоторый массив длин префиксов, упорядоченный по возрастанию. Затем бинпоиском найдем наибольший по длине префикс, который находится где-то внутри (преверка осуществляется за O(n)). Итого сложность решения .

На самом деле, если в предыдущем решении присмотреться к массиву длин префиксов, то получим ни что иное, как p[n], p[p[n]] и т.д. в обратном порядке. Из первого решения мы знаем, что либо p[n], либо p[p[n]] ответ. Поэтому заходили даже такие наивные решения, как второе без бинпоиска, то есть просто проверка всех префиксов в порядке уменьшения длины. Это решение работает за O(n).

Также возможны решения с использованием z-функции.

div2 E. div1 C. Во первых, понятно, что каждую из операций i, j имеет смысл делать не более одного раза, а порядок операций не важен. По сути, всю последовательность команд можно представить себе как булеву матрицу A размера n × n, где a_ij = 1 означает, что мы выполняем команду i, j, и a_ij = 0 означает, что мы ее не выполняем.

Опишем способ построения такой матрицы.

Пусть изначальная картинка --- это матрица G. Еще заведем матрицу B, в которой будем хранить все изменения, которые получились в результате выполнения операций.

Для верхней половины матрицы G без диагонали мы будем двигаться построчно сверху вниз. Каждую строчку будем просматривать справо налево. Заметим, что для каждой рассматриваемой позиции никакие команды, соответствующие еще не рассмотренным позициям, не влияют на текущую позицию. Поэтому, если мы обнаруживаем несоответствие в текущей позиции i, j в матрицах G и B, то мы обязаны выполнить команду i, j: ставим в A a_ij = 1, а в B меняем отрезки (i, i) - (i, j) и (j, j) - (i, j).

Для нижней половины матрицы G без диагонали делаем все абсолютно симметрично. В конце проходимся по самой диагонали --- с ней должно быть все понятно.

Итак, для каждой матрицы G мы всегда и однозначным способом можем получить матрицу A. Это означает, что именно здесь и достигается минимум требуемых операций. Таким образом, ответ можно построить так: из G строим A и выводим количество единиц в A (в первой версии задачи был еще и вывод сертификата --- самой последовательности команд. Но из-за большого вывода от этого пришлось отказаться).

Осталось решить небольшею проблемку. Описанный выше способ позволяет сделать из G A за O(n³), что несколько долго. Ускорим его до O(n²). Рассмотрим в матрице B верхнюю половину без диагонали. В процессе выполнения алгоритма все столбцы ниже уже рассмотренных позиций всегда принимают одно и то же значение, а все значения выше нам уже никогда не понадобятся. Поэтому Вместо матрицы B можно использовать лишь один массив, в котором хранятся цвета столбцов и выполнять перекраску за O(1) вместо O(n). Эта оптимизация и дает нам решение за O(n²).

div1 D. Представим число в фибоначчиевой системе счисления. В двух словах что это такое: i-му числу Фибоначчи соответствует i-ый бит. Например, число 16 запишется как 3+13 или 100100. Любое натуральное число можно представить в таком виде, при этом в записи никогда не встретятся две единицы подряд. Таким образом можно представить число только одним способом (будем называть такое разложение каноничным). Нам же нужно посчитать количество разложений, когда две единицы могут стоять подряд.

Канонично разложить можно просто сгенерировав достаточно много чисел Фибоначчи (около 90) и потом жадно отнимая он данного числа начиная с самых больших.

Запомним на каких местах стоят единицы в каноничном разложении и сохраним их в массив s в порядке возрастания. Каждую из единичек можно раскладывать в 2 единички. Это выглядит примерно так:

1000000001 // начально число;
0110000001 // раскладываем
0101100001 // первую единичку
0101011001 // всеми возможными
0101010111 // способами

При этом через некоторое количество операций упремся в впереди стоящую единичку (или в конец числа). Однако эта единичка тоже может быть разложена, но она может "сдвинуться" только на 1 бит.

Заведем dp1[i] --- количество способов разложить число, состоящее из i последних единичек нашего числа при условии, что самая первая единичка ни во что не раскладывается. также заведем dp2[i] --- количество способов разложить число, состоящее из i последних единичек нашего числа при условии, что самая первая единичка обязательно раскладывается.

Пересчитывается эта динамика очень просто

dp1[0] = 1, dp2[0] = 0
dp1[i] = dp1[i - 1] + dp2[i - 1]
dp2[i] = dp1[i - 1] * [(s[i] - s[i - 1] - 1) / 2] + dp2[i - 1] * [(s[i] - s[i - 1]) / 2]
где [x] --- округление вниз.

Ответом будет dp1[k] + dp2[k], где k --- общее число единичек. Итого решение за для одного теста.

div1 E. Рассмотрим все разбиения доски 7 × 8 на доминошки. Их немного --- всего 12988816 (это можно узнать, запустив несложный перебор)

Кроме того, рассмотрим всевозможные "покраски" поля 7 × 8 (то есть количества квадратиков каждого из цветов) и найдем количество разбиений этих покрасок на множество пилюль 10 типов. В худшем случае получим 43044 разбиений (это число можно получить другим перебором).

Первая половина решения состоит в том, чтобы перебрать все разбиения доски на доминошки и найти все множества пилюль, которые получаются в результате таких разбиений. Их будет не более 43044.

Во второй части решения для каждого из них надо попробовать наиболее оптимальным образом распределить имеющиеся пилюли так, чтобы как можно больше цветов совпало.

Построим граф из 4 долей - исток, 1я доля на 10 вершин, 2я доля на 10 вершин, сток. Между всеми парами вершин из соседних долей протянем ребра. Из истока в 1ю долю назначим пропускные способности равные количеству имеющихся пилюль каждого типа. Из 2й доли в исток назначим пропускные способности равные количеству пилюль каждого из типов в текущем разбиении. Из 1й доли во вторую назначим бесконечные пропускные способности и стоимости, равные количеству НЕсовпадающих цветов типов пилюль (это какие то числа от 0 до 2). Пустим по графу максимальный поток минимальной стоимости --- он и найдет оптимальный ответ. Из всех разбиений найдем самый оптимальный ответ и сохраним его.

Третья часть решения состоит из восстановления ответа по потоку в оптимальном разбиении.

Во второй части решения MCMF можно заменить на обычный максимальный поток. Нужно лишь понять, что сначала MCMF будет всегда идти по ребрам стоимости 0, пока полностью не насытит их. Поэтому можно сначала жадно вручную насытить такие ребра, после него оставить только ребра стоимости 1 и на полученном графе запустить просто MaxFlow.

Сложность решения оценить сложно, но сразу видно, что оно заходит. Самое первое решение жюри на C++, написанное как попало, работает 1 с. Несколько более вдумчивые варианты работают 0,4 с, но их, при желании, можно и еще ускорить.