Codeforces Beta Round #97: разбор

№	Пользователь	Рейтинг
1	tourist	3985
2	jiangly	3741
3	jqdai0815	3682
4	Benq	3529
5	orzdevinwang	3526
6	ksun48	3489
7	Radewoosh	3483
8	Kevin114514	3442
9	ecnerwala	3392
9	Um_nik	3392

№	Пользователь	Вклад
1	cry	169
2	maomao90	162
2	Um_nik	162
2	atcoder_official	162
5	djm03178	158
6	-is-this-fft-	157
7	adamant	155
8	awoo	154
8	Dominater069	154
10	nor	150

Представляю разбор задач Codeforces Beta Round #97. Если есть какие-то вопросы или пожелания --- пишите в комментариях.

136A - Подарки (A Div 2)

В этой задаче нужно было просто считать перестановку и вывести обратную к ней. Для этого просто при считывании i-го по счету числа, которое равно a поместим i в ячейку массива с номером a. После этого выведем полученный массив.

Сложность решения O(N).

136B - Тернарная логика (B Div 2)

Легко понять, что ответ всегда определяется однозначно. Для того чтобы его найти, можно ввести аналог операции вычитания без переноса разрядов. От каждого разряда числа c, записанного в троичной системе счисления отнимем соответствующий разряд числа a и результат вычитания в каждом разряде возьмем по модулю 3. Полученное число и будет искомым b, таким что a tor b = c.

Сложность решения O(logC + logA).

136C - Замена (C Div 2)

135A - Замена (A Div 1)

Если наибольшее число в массиве равно 1, заменим его на 2, в противном случае заменим его на 1. После чего отсортируем массив и выведем его. Легко понять, что массив, полученный таким образом и будет оптимальным.

Сложность решения O(NlogN).

136D - Прямоугольник и квадрат (D Div 2)

135B - Прямоугольник и квадрат (B Div 1)

Переберем все возможные разбиения точек на 2 множества по 4 элемента. Для первого множества нужно проверить, образует ли оно квадрат, а для второго --- прямоугольник.

Для того чтобы проверить, лежат ли 4 точки в вершинах прямоугольника, достаточно перебрать все перестановки последних трех точек и затем убедиться, что каждые 2 последовательных отрезка, соединяющих последовательные точки, образуют прямой угол. Это можно сделать используя тот факт, что скалярное произведение двух векторов равно нулю тогда и только тогда, когда угол между ними --- прямой.

Для проверки того, лежат ли 4 точки в вершинах квадрата, достаточно проверить что эти 4 точки лежат в вершинах прямоугольника и то, что 2 соседние стороны равны.

136E - Ноль-один (E Div 2)

135C - Ноль-один (C Div 1)

Для начала решим задачу когда нет ни одного знака вопроса. Пусть в числе a единиц и b нулей. Легко видеть, что если a < b, то исход 00, поскольку первый игрок может каждым своим ходом выбирать единицы, пока они не закончатся, что произойдет до окончания игры вне зависимости от ходов второго игрока. Аналогично, если a > b + 1, то исход 11.

Если же a = b или a = b + 1, то исход либо 01, либо 10. Это можно объяснить тем, что первому игроку всегда имеет смысл брать единицы, поскольку в противном случае игра сведется к 00, что хуже для него, чем любой из оставшихся вариантов. Аналогично, второму игроку имеет смысл брать только нули. Также можно заметить, что первый игрок должен каждый раз брать первую единицу с начала, так как это не ухудшит ответ для него. Второй игрок должен брать первый ноль с начала. Следовательно, последнюю цифру в строке вообще никто не возьмет. А значит, если она равна 1, то исход будет 01, иначе 10.

Итак, мы научились определять, кто выиграет при отсутствии знаков вопроса. Теперь предположим, что у нас a единиц, b нулей и c знаков вопроса. Для того чтобы проверить, может ли получиться исход 00, достаточно все знаки вопроса заменить нулями, т.е. проверить, что a < b + c. Аналогично, для проверки исхода 11, нужно проверить равенство a + c > b + 1.

Покажем как проверить, возможен ли исход 01. Если последний символ строки 0, то этот исход не возможен. Если последний символ ?, то можно заменить его на 1, тем самым уменьшив c на 1 и увеличив a на 1. Пусть теперь мы x знаков вопроса заменяем на единицы и с - x знаков вопроса заменяем на нули. Тогда можем записать, что x + a = b + c - x + (a + b + c) mod 2. Отсюда получаем, что x = (b + c - a + (a + b + c) mod 2) / 2. Если получившееся значение x лежит в диапазоне от 0 до c, то исход 01 возможен, иначе --- нет.

Аналогичным образом проверим исход 10.

Сложность решения O(N).

135D - Цикл (D Div 1)

Заметим, что единственный вариант когда внутри цикла нет ни одного нуля, это когда цикл состоит из 4 клеток и образует квадрат 2х2 из единиц. Наличие такого квадрата в таблице нужно проверить отдельно. После этого будем считать, что внутри цикла всегда есть хотя бы один ноль.

Рассмотрим любой ноль из таблицы. Если он смежный по стороне или углу с еще одним нулем, то этот ноль не может в одиночку входить в цикл, так чтобы внутри больше нулей не было. Следовательно, этот ноль может входить в цикл только вместе со всеми смежными с ним нулями. Продолжая рассуждения можно показать, что этот ноль может входить в цикл только с нулями, лежащими с ним в одной компоненте связности. Здесь смежность определяется как наличие общей стороны или общего угла у клеток.

Выделим все компоненты связности. Если компонента связности граничит с краями таблицы, то она не может лежать целиком в цикле, а значит мы ее пропускаем. После этого, для каждой конкретной компоненты связности найдем все смежные с ней единицы. По условию, эти единицы должны образовывать связную область, а также каждая единица из найденного набора должна иметь общую сторону ровно с двумя другими единицами из этого набора. Отдельно проверять то, что внутри области единиц нет других единиц уже не требуется, поскольку это и так гарантируется способом нахождения этой области.

При аккуратной реализации сложность решения получается O(NM).

135E - Слабая подпоследовательность (E Div 1)

Ключевым наблюдением является то, что искомая самая длинная подстрока является либо префиксом, либо суффиксом строки s. Кроме того, если, например, она является префиксом, то найти ее можно следующим образом. Будем двигаться начиная с конца строки по направлению к началу, попутно запоминая все пройденные символы. Как только какой-то символ встретился второй раз, мы останавливаемся. Префикс с концом в позиции, где этот символ встретился второй раз и будет искомой самой длинной подстрокой. Аналогично эта подстрока ищется и в случае, когда она является суффиксом.

Посчитаем количество строк, у которых сама длинная подстрока нужного нам вида является суффиксом. Переберем сколько символов в начале строки идут до повтороной встречи какого-то символа. Пусть это количество равно t. Очевидно, что t не превышает k, поскольку в префиксе длины t все символы различны. Следует рассмотреть следующие 2 случая:

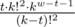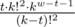1. Если t ≤ w - 1. Первые t символов различны, затем идет символ, который встречался среди первых t символов. После него идет еще w - 1 символ. Следует также учесть, что последние t символов также должны быть различны, поскольку иначе префикс длины большей чем w будет также слабой подпоследовательностю. Получаем, что соотв. слагаемое равно $\text{[math]}$ .

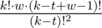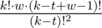2. Если t > w - 1. Первые t символов различны, затем идет символ, который встречался среди первых t символов. После него идет еще w - 1 символ. Последние t символов должны быть различны, но теперь этот "хвост" из t символов пересекается с префиксом из t символов. Соответствующее слагаемое равно $\text{[math]}$ .

Просуммировав по всем t от 1 до k, получим искомое количество строк, где самая длинная подстрока нужного нам вида является суффиксом длины w.

Аналогично ищется количество строк, у которых самая длинная подстрока нужного нам вида является префиксом. Единственное отличие состоит в том, что мы должны следить чтобы первые t + 1 символов нашей строки были различными, во избежание повторного учета строк, где и первые, и последние t символов различны. С учетом этого, формулы станут:

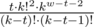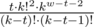1. Если t + 1 ≤ w - 1, то слагаемое равно $\text{[math]}$ .

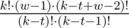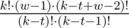2. Если t + 1 > w - 1, то слагаемое равно $\text{[math]}$ .

Суммируем по всем t от 1 до k - 1 и получаем искомое количество строк, у которых самая длинная подстрока нужного нам вида является префиксом.

Для быстрого подсчета всех формул нужно также предпосчитать факториалы чисел 1..k, а также обратные к ним значения.

Сложность решения O(K) или O(K· log(MOD)), в зависимости от того, как считались обратные значения к факториалам.

В качестве бонуса для тех, кто дочитал разбор до конца, напишу как можно довольно просто и за линейное время посчитать обратные значения для всех чисел от 1 до N по простому модулю P (P > N). Думаю, это будет полезно для тех, кто не слышал об этом приеме.

Итак, рассмотрим простое тождество (операция % означает взятие остатка по модулю), после чего сделаем над ним несколько простых операций.

$\text{[math]}$

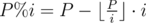
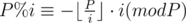
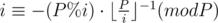
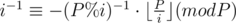
Отсюда получаем, что для вычисления i^- 1 нам нужно знать лишь (P%i)^- 1, что меньше i. Значит, подсчитать обратные значения последовательно для всех чисел от 1 до N можно за O(N).

Комментарии (24)

Показать архивные | Написать комментарий?

herr_bilbo

13 лет назад, # |

Легко понять, что ответ всегда определяется однозначно.

Извините конечно нуба, но что-то я не понимаю, почему ответ лишь один? объясните, пожалуйста.

→ Ответить

dalex

13 лет назад, # ^ |

Переводим в троичную систему и понимаем, что вычисление одного из разрядов не влияет на остальные.

Благодарю, теперь дошло:-)

В задаче про прямоугольник и квадрат еще можно было проверить, что длины сторон правильные и что площадь соответствует этим длинам сторон.

KADR	13 лет назад, # ^ \| 0 Есть много способов, как проверить, является ли фигура прямоугольником или квадратом. Я описал лишь один из них. → Ответить

Jokser

D-шка оказывается очень просто решалась. Спасибо за разбор!

ivan.popelyshev

Моё решение в Е было более извращённым: я неправильно прочитал условие и подумал что надо считать количество строчек где НЕТ таких подстрок длины w, из-за этого в моём коде появилось быстрое возведение в степень. Обнаружив что был неправ, я взял результат для w+1 и вычел результат для w.

KADR	13 лет назад, # ^ \| 0 То-то я смотрю, что оба прошедших на контесте решения не похожи на мое. → Ответить

bapcoi

Thanks for your editorial, it helps much.

taserghar

Div 2 Problem E was really a good tricky problem....and I didn't catch that .... :(

Ziklon

good set :)

AlfaCoding

Can someone tell me how to find a recent blog（may be several weeks ago） that i forget its title and its author？Thanks a lot~:)

drbitboy

Thanks for the review!

Heh. You sure are right about being careful on 135D Div 1 Cycle.

I *thought* I had a O(NM) solution, but I was keeping a vector< set<int> > with a total of something like (NM + some %age) entries, of the 1s and 0s. I finally realized, after reading your approach, which was basically the same as mine, that I was doing almost nothing with the sets once I loaded them up! When I dropped the sets, the submitted code finished within the time limit.

Also, isn't the complexity is more like O( (NM)^1.x ), because each '1' may bound more than one of each set of connected 0s?

What really amazes me is how someone implements this - successfully - during the 2-hour competition. I've been working on it on and off for almost a week and finally had something close this afternoon.

Thanks again,

KADR

>Also, isn't the complexity is more like O( (NM)^1.x ), because each '1' may bound more than one of each set of connected 0s?

The complexity is still O(NM). One can notice that each '1' can be adjacent to not more than 4 connected components of zeroes. It means that in total we'll process all '1's not more than 4NM times, which is O(NM).

phantom11

In the problem Zero-One's editorial one of the statement is
"Then the following equality must hold: x + a = b + c - x + (a + b + c) mod 2"
Why is this so??

riadwaw

b+c-x+a+b+c = 2b+2c+(a-x) = a-x = a-x+2x = a+x

We can add 2n for every integer n

I meant to ask how to we get that inequality and how can we use it in the given problem.Could you elaborate a bit....

The number of ones is x + a. The number of zeroes is b + (c - x). As it was said in the editorial, the answer is 01 or 10 iff the number of ones = the number of zeroes or the number of ones = the number of zeroes + 1 (depends on parity of n). It means that x + a = b + (c - x) + (n mod 2) which is the same as x + a = b + (c - x) + ((a + b + c) mod 2).

uprising_rk

7 лет назад, # |

i am able to understand 136A..plz explain

SummerSky

7 лет назад, # ^ |

(guess that you mean 'unable'...)

I think this problem means that the i-th person gives a present to the p_i-th person, and thus the p_i-th person receives a present from the i-th person. Therefore, we can adopt an array a[n] and set a[p_i] = i (p_i is just another positive integer j), and finally it suffices to output array a[n].

roll_no_1

5 лет назад, # |

← Rev. 6 →

An easier way to solve Div1 B / Div2 D is to check the following conditions instead:

For a rectangle: Fix the 4 vertices as $$$A, B, C$$$ and $$$D$$$. Now, we have to check the following 3 conditions:

1. |AB| = |CD|

2. |AC| = |BD|

3. |AD| = |BC|

The first 2 conditions ensure that it's a parallelogram, and the last condition ensures that it's a rectangle

For a square: Fix the 4 vertices as $$$A, B, C$$$ and $$$D$$$. Now, we have to check the following 2 conditions:
```
1. It is a rectangle, by calling the function used to check for a rectangle.

2. |AB| = |AC|
```

To avoid precision issues, we can compare square of distances instead, which can be computed only using integers.

Code.