yahooo хочет знать, можно ли (если можно, то как) находить произведение последовательного ряда чисел фиббоначи, т.е F1F2F3...Fn за время ассимптотически небольшее O(logN)? (N не больше инта)
я нашел много информации по числам фибоначчи, но так и не нашел, как это делать =(
UPD: конечно же, произведение должно быть найдено по модулю, который может быть любым, неменьше 2 и не превосходит инта
UPD2: ну грубо говоря, мне нужно находить не это, а то, с какого момента это произведение по модулю равно нулю... может так будет проще
Фишка в том, что без модуля их там всего порядка пары тысяч первых значений в память влезет.
Без модуля - тоже важно какой модуль. Точнее, важно, имеет ли он вид 4k + 1, или 4k + 3. По какому модулю?
UPD: Ой-ой-ой. Какой я бред сказал. Во-первых, я, конечно, имел в виду, необходимость того, что 5 является квадратичным вычетом. Мне показалось, что тогда из того, что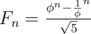
, можно вывести что-то хорошее. Похоже, что нет.
На самом деле, можно подумать на тему того, что есть такое (a + b)(a2 + b2)...(an + bn) после раскрытия скобок, и как его быстро посчитать. Быстрее чем за линию ничего в голову пока не приходит Можно попытаться учитывать то, что ab = 1 в нашем случае.
Наверно так Натуральное число N является числом Фибоначчи тогда и только тогда, когда 5N2 + 4 или 5N2 − 4 является квадратом.
Это похвально :-)
Аа.. Ну так бы и сказали. Тогда вам копать в сторону периода Пизано.
Вот, например, хороший абзац:
Для простого числа p и целого числа k ⩾ 1 выполняется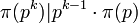
. Более того, для всех точных степеней простых чисел от 1 до миллиона выполнено равенство 
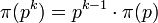. Но до сих пор неизвестно, на всегда ли выполнено это равенство, и существуют ли такое p, что π(p2) = π(p).
До миллиона-то вам за глаза хватит.
Дальше воспользоаться мультипликативностью. А дальше научиться считать π(p). А это эквивалентно тому, что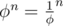
, т. е. φ2n = 1, а это уже задача поиска порядка числа по простому модулю. Это уже баян.
да я читал это, но 2 вопроса:
1) только до миллиона, а простые в инте могут быть и довольной большие (~2млрд), ну допустим, что для 2млрд это выполняется я еще готов поверить, но
2) как я узнаю допустим pi(p)? тем более если p~2млрда?
пока писал это, ты проапдейтил свой коммент, в связи с этим, что такое мультипликативность?
Читаем мой пост чуть ниже - я для простого числа дописал.
Для взаимно простых a и b π(ab) = [π(a);π(b)]. Вот такая тут мультипликативность.
блин, такое страшное слово, означает этот факт, ну хорошо, спасибо)
честно говоря не очень понял последнее, ну сам попытаюсь найти, спасибо за помощь)
Cреди k+1 последовательных чисел Фибоначчи найдется число, делящееся на k, для любого простого k.
Вас устроит перебор k+1 первых чисел?блин, точно, я че то не подумал даже....
у какой-то у товарища фальшивый Капитан Очевидность
да забей, мне же нужно решить проблему, не тебе, я думаю у тебя своих проблем хватит, вместо того чтобы это копать
если конечно из личного интереса, то пожалуйста
в связи с этой темой:
читаю на википедии эту статью, одно из свойств:
Если p — нечётное простое число, то π(p) является делителем , p - (p/5), где (p/5) — символ Лежандра.
проверяю для p = 3:
(3/5)=-1, если я не ошибся
p - (p/5) = 3 - (-1) = 4
π(3) = 8, но как так, по свойству π(3)должно являться делителем 4х!
я где то натупил?
извините за оформление...
Back
то, спасибо за ссылку конечно, но я хотел бы все таки сам решить, а там уже все решение как я понял
P.S. теперь я просто понимаю, что ту задача которая передо мной стоит (не так что в теме), я могу и сам решить покопавшись немного в каких-либо статьях
п.с. странно что факт в примечании вынесли в примечания, т.к. он нифига не примичание, автор этой статьи позиционировал его как основной результат, известный про период писано :)
оно очень похоже на верное, но его доказательство должно быть нетривиальным и довольно интересным, потому что вот здесь была задача про период Писано и не одна из докладывавших команд не доказала линейность
*full of sarcasm*Но спасибо, что помогли человеку ее решить.
Этот.
ну даже если она и отсюда,
1) я же не попросил конкретно решить ее, тут еще и свести надо
2) если бы я хотел я бы посмотрел по ссылке и думаю, у меня было бы 160 по ней уже (судя по тому что, этот сайт вроде международный форум АСМ программистов)
2. От того, кто клянчил у других решение задачи на GCJ вполне ожидаемый ответ. Но ведь никто не будет спорить что это как минимум некрасиво - просить подсказку на задачу с идущего контеста.
согласись, я мог бы просто банально решение найти, это было бы еще более некрасивее
(хочешь верь, хочешь нет) но ничего нового я не узнал, сколько мучался целый день, со свойствами в вики, тестинг раунд написал, снова начал мучаться и что-то стало получаться...
по крайней мере я себя виноватым не считаю по 2 вышеуказаным причинам...