Здавствуйте! Все знают, что |MinCut| = |MaxFlow| в сети. Кто знаком с темой может прокрутить вниз, там вопрос.
[newbie mode] Как найти какие именно ребра являются разрезом? Тут вроде тоже все понятно, разделим множество вершин на два множества: S — множество достижимых вершин из истока по ненасыщенным ребрам и T = V / S. Ребра, которые соединяют вершины из разных множеств и будут одним из ответов.
Как найти вершинный разрез? Учили так: разделим каждую вершину v на 2 вершины: v1 для входящих и v2 для выходящих. Сделаем так же ребро v1 - > v2 с пропускной способностью 1. Далее найдем макс.поток и размер потока будет равен минимальному вершинному разрезу. Но как теперь найти ответ?
В задаче на USACO trainings (telecow, 5.4.5) проходит такое решение для |V| ≤ 100, |E| ≤ 600:
Будем по очереди удалять ребро между v1 и v2 для каждой вершины и будем заного находить поток. Если поток уменьшился на единицу, то эта вершина входит в раздрез.
Мне не очень понравилось это решение, ведь делая это алгоритмом Диници, это будет работать не мало: O((|V||E|)2), где кол-во вершин увеличивается в 2 раза, а кол-во ребер примерно в 4 раза(обратные ребра и по 2 ребра на каждое, так как ребра не ориентированны), получается где-то 100 * 2 * 600 * 4 в квадрате итераций? Сначала я испугался такой цифры, но вспомнив, что ребра с пропускной способностью в единицу делают ее еще быстрее, то выходит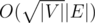 
помножиное на |V| вызовов, то выходит около 6 * 106, что приемлемо. [/newbie mode]
Но как находить вершинный разрез, когда вершин и ребер еще больше? Есть ли более оптимальное решение?
А, вопрос как найти вершинный разрез после преобразования графа. Вроде, найдем реберный разрез получившегося графа. Дальше два варианта — либо ребро "внутри" одной вершины, либо нет. Если внутри — все понятно, режем вершину. Если нет — разрезающее ребро одной вершиной на истоке (до "верхней" существует поток размером хотя бы 2, значит, она исток), удалим другую.
Извините, но я ничего не понял. Мы это делаем в графе с уже разводенными вершинами? Зачем нам вообще резать ребра не в вершине?
Итак, мы раздвоили вершины и построили в новом графе разрез. У нас есть два типа ребер — старые и новые. Реберный разрез может содержать ребро любого из этих типов. Дальше по тексту.
а можно еще подробнее? Мы уже построили поток в графе из раздвоенных вершин. Мы хотим узнать, какие именно вершины составляют разрез.
Чем отличаются старые ребра от новых? Два варианта, внутри вершины и нет. Откуда у нас эти варианты? Как мы их нашли? Блин, я глуп и не понимаю, можно "для глупых"? По шагам?
новые рёбра, это те что v1 -> v2, которые мы добавили при раздвоении вершин. старые, это те что были в исходном графе, и перенесены сюда (x2 -> y1), если было ребро (x -> y). В графе с раздоенными вершинами найдем мин разрез, ребра в него вошедшие, могут быть либо "новыми" т.е. теми, что сделаны нами для раздвоения вершин, либо "старыми" т.е. теми что были в исходном графе, и перекочевали в новый. поэтому "два варианта" — старое ребро, либо новое. в общем из разреза нас интересуют только ребра между раздвоенными вершинами, и вершины исходного графа, рёбра раздвоители которых попали в мин разрез нового графа, попадают в вершинный разрез исходного графа.
Не о том. Читать надо до конца и внимательней.
Из-за маленького размера экрана нетбука я не могу ответить на сообщения mr.goo.gl_SsAhv поэтому отвечу здесь:
Спасибо, стало понятнее. Теперь мы нашли поток в новом графе. Опять пометили вершины от истока. Возьмем все ребра, которые соединяют вершины из разных множеств.
Если ребро внутри вершины, то закидываем ее в ответ, а что делаем, если это обычное ребро?
Может, нужно просто все остальные ребра сделать бесконечной пропускной способности, тогда они не попадут в разрез?
Так и надо делать? Тогда спасибо. Таким образом будет найден любой минимальный разрез, ведь так? А есть способ найти лексиграфически первый и подобное?
С ходу не знаю, скорее всего как-то можно добиться лексикографической первости в каком-то смысле :)
Если сделать остальные бесконечной пропускной, главное — правильно обработать полученный ответ бесконечность и написать правильный поиск потока, чтобы не заТЛило ;)
Upd. Там выше пруф, что если это обычное ребро при пропускной 1, то в разрезе конец этого ребра (т.к. начало этого ребра вершина S).
Да, пруф вроде верный. Из него кстати следует (да в общем и так понятно), что можно вместо бесконечности сделать 2, тогда точно нет проблемы с ТЛем.