mukel's blog

Suffix Arrays
By mukel, 13 years ago, In English

This is a simple, bus fast implementation, it builds both, the suffix array, and the LCP (Longest Common Prefix) table. Have fun with it.

/*
Suffix array O(n lg^2 n)
LCP table O(n)
*/
#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

#define REP(i, n) for (int i = 0; i < (int)(n); ++i)

namespace SuffixArray
{
	const int MAXN = 1 << 21;
	char * S;
	int N, gap;
	int sa[MAXN], pos[MAXN], tmp[MAXN], lcp[MAXN];

	bool sufCmp(int i, int j)
	{
		if (pos[i] != pos[j])
			return pos[i] < pos[j];
		i += gap;
		j += gap;
		return (i < N && j < N) ? pos[i] < pos[j] : i > j;
	}

	void buildSA()
	{
		N = strlen(S);
		REP(i, N) sa[i] = i, pos[i] = S[i];
		for (gap = 1;; gap *= 2)
		{
			sort(sa, sa + N, sufCmp);
			REP(i, N - 1) tmp[i + 1] = tmp[i] + sufCmp(sa[i], sa[i + 1]);
			REP(i, N) pos[sa[i]] = tmp[i];
			if (tmp[N - 1] == N - 1) break;
		}
	}

	void buildLCP()
	{
		for (int i = 0, k = 0; i < N; ++i) if (pos[i] != N - 1)
		{
			for (int j = sa[pos[i] + 1]; S[i + k] == S[j + k];)
			++k;
			lcp[pos[i]] = k;
			if (k)--k;
		}
	}
} // end namespace SuffixArray

Another using hashing


namespace HashSuffixArray
{
	const int
		MAXN = 1 << 21;

	typedef unsigned long long hash;

	const hash BASE = 137;

	int N;
	char * S;
	int sa[MAXN];
	hash h[MAXN], hPow[MAXN];

	#define getHash(lo, size) (h[lo] - h[(lo) + (size)] * hPow[size])

	inline bool sufCmp(int i, int j)
	{
		int lo = 1, hi = min(N - i, N - j);
		while (lo <= hi)
		{
			int mid = (lo + hi) >> 1;
			if (getHash(i, mid) == getHash(j, mid))
				lo = mid + 1;
			else
				hi = mid - 1;
		}
		return S[i + hi] < S[j + hi];
	}

	void buildSA()
	{
		N = strlen(S);
		hPow[0] = 1;
		for (int i = 1; i <= N; ++i)
			hPow[i] = hPow[i - 1] * BASE;
		h[N] = 0;
		for (int i = N - 1; i >= 0; --i)
			h[i] = h[i + 1] * BASE + S[i], sa[i] = i;

		stable_sort(sa, sa + N, sufCmp);
	}

} // end namespace HashSuffixArray
  • Vote: I like it
  • +31
  • Vote: I do not like it

Comments Comments (45)
| Write comment?
»
13 years ago, # |
  Vote: I like it -33 Vote: I do not like it

Another quick to code approach, O(n^2 lg n)


#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

const int
	MAXN = 1 << 17;

char text[MAXN];
int sa[MAXN];

bool sufCmp(int i, int j)
{
	return strcmp(text+i, text+j) < 0;
}

int main()
{
	scanf( "%s", &text );

	n = strlen(text);
	for (int i = 0; i < n; ++i)
		sa[i] = i;

	sort(sa, sa + n, sufCmp);

	for (int i = 0; i < n; ++i)
		printf( "%s\n", text + sa[i] );

	return 0;
}
→ Reply
  • »
    »
    13 years ago, # ^ |
    ← Rev. 2   Vote: I like it +14 Vote: I do not like it

    It is too stupid. There is another stupid way to construct suffix array for O(n * log(n) * log(n)). We need to sort suffixes using compare operation for O(log(n)). To compare substring for O(log(n)) we need to use polynomial hashes and binary search. With such a slow compare operation it is more efficient (20-30 percent faster) to use merge-sort or std::stable_sort. I have used this technique several times for building suffix array on strings with length 10^5-3*10^5 characters.

    → Reply
»
13 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Can someone post some simple implementation for linear construction of suffix array?

→ Reply
»
13 years ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

which is faster here? I mean hash version or non-hash version?

→ Reply
  • »
    »
    13 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    Each of them is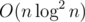 . There is an algorithm which works in .

    → Reply
    • »
      »
      »
      13 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      can you please give any reference or explanation? Thanks

      → Reply
      • »
        »
        »
        »
        13 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        Google "suffix array". in a nutshell: we need to use "radix sort"(goolge it) in first buildSA().

        → Reply
    • »
      »
      »
      13 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      There is an algorithm which works in O(n).

      → Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can you please explain the buildSA function in detail? What exactly is the sufCmp function trying to achieve?

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    For the first algorithm: In each step you calculate the order of suffixes of length "gap" so in the first iteration (iteration 0) you just sorts all the suffixes by the first letter, in the second by 2 letters, then by 4, 8, 16, 32 ... 2^k If you know the order of suffixes using only it's first 2^k letters then (using that information) you can calculate the order using first 2^(k + 1) letters; this is because each suffix of 2^(k + 1) can be seen as 2 contiguous suffixes of length 2^k of which you already have an "order" established.

    For the second, you use binary search to find the first position where two suffixes are different, and then just compare those 2 chars. But this implementation using hashing can fail for some well known cases, that means that your solution could be easly hacked in a real CF round.

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      I don't understand how you are implying this statement "If you know the order of suffixes using only it's first 2^k letters then (using that information) you can calculate the order using first 2^(k + 1) letters; this is because each suffix of 2^(k + 1) can be seen as 2 contiguous suffixes of length 2^k of which you already have an "order" established."
      and
      can you please explain below 3 lines
      REP(i, N — 1) tmp[i + 1] = tmp[i] + sufCmp(sa[i], sa[i + 1]);
      REP(i, N) pos[sa[i]] = tmp[i];
      if (tmp[N — 1] == N — 1) break;
      // if sa[] stores suffix indices then what does pos[] stores
      and
      essence behind LCP code

      → Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If I'm not wrong then this is an O (n) implementation of Suffix Array and Lcp. And it's pretty simple too. (Is it really? -_-)

P.S. The code is untested.

→ Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    It is O(n lg n). It uses radix sort instead of quiksort, saving just a lg n factor.

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Isn't it an implementation of DC3 algorithm? Or I've been mistaken....

      → Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    what is the kasaiLCP () function ? what is its output ? in the other words, if we want to calculate the lcp(i,j) what should we do ?

    LCP[i] = lcp(i,i-1) ?

    → Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    one more thing !

    i test this code , but it constructed false SA array for case "aaa" . for every string with all characters same and odd length , it produce wrong answer , can you help me what's going wrong ?

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      This N = strlen (str) should be N = strlen (str) + 1. I think everything else is fine. The SA and LCP array here are 1-indexed. And your assumption about LCP array is right. Please inform if it isn't still working.

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        when i changed this line of code , it worked, but all indices in SA array shifted one ! i can't test whether it's compeletly OK or not. it seems a bit modification still needed.

        → Reply
        • »
          »
          »
          »
          »
          11 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Told you they are 1-indexed, not 0. Then try this one.

          → Reply
»
11 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Anyone wants to give me an easy problem (wanna exercise a bit :D) solvable by suffix array?

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    try this one and also Hidden Password

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thanks the first one is actually where I learned it from :D Thx for the second one too. but isn't there timus alternative for this problem? (timus is the only online judge I approve :]] )

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        I don't know alternative link for timus ! anyway, I could find many links of the suggested problems in the first tutorial in OJs. Search the sample problems in tutorial, you'll find many of them.

        → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you please explain the solution of Hidden Password using Suffix Array.

      This idea of mine is giving WA. First I am concatenating the string with itself and now I find both the suffix array and LCP of this new string. The answer is the one which has the maximum value in the suffix array having the same LCP as that of the least value in the suffix array.

      Please can you tell me where am I going wrong.

      Thanks.

      → Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    http://mirror.codeforces.com/gym/100133

    → Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Anyone knows a way of implementing this in a parallel way? I know of this http://link.springer.com/chapter/10.1007%2F11846802_12#page-1 DC3 parallel implementation explained in this paper, but I am seeking for a code example... I am not really good with threads and I need this for a project.

→ Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    DC3 is an overkill (depending on the task) and is practical for relative large inputs because its high constant factor.

    For the n lg^2 n method described in my post, every line can be done in parallel:

    1) sort(sa, sa + N, sufCmp);

    2) REP(i, N — 1) tmp[i + 1] = tmp[i] + sufCmp(sa[i], sa[i + 1]);

    3) REP(i, N) pos[sa[i]] = tmp[i];

    1) Sorting is easy, eg use parallel_sort instead 2) Partial sums computation, this is also quite known, maybe you can use parallel_partial_sum instead. 3) Just parallelize the for (many libraries offer this feature, I'm almost sure that C++ (the newest standard with parallel extensions) support this also), each case is independent from the others.

    At the end the algorithm scales nicely without any heavy modification.

    → Reply
»
11 years ago, # |
  Vote: I like it +10 Vote: I do not like it

Awesome post! Thank you for sharing.

→ Reply
»
11 years ago, # |
← Rev. 2   Vote: I like it +14 Vote: I do not like it

--

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Code in edit doesn't work, you can't modify pos[] to calculate tmp[], because the comparison uses pos[].

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      Right! I deleted my comment after I figured out what you are saying :) Could you please say why your LCP algorithm runs in O(n) time? Post is great but can be made greater if you take the time to annotate it with some comments here and there. Thanks.

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

As I am recently learning suffix array — I don't understand why you use "for (gap = 1;; gap *= 2)" this gap variable, and why you increasing the value of i and j as i += gap, j += gap in "bool sufCmp(int i, int j)" function. :)

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    At each step suffixes are sorted based on the first 2^gap letters (from now this will be called the suffix length). To compare two suffixes (i and j) of length 2^(gap+1), you use the information of the previous suffix order (2^gap). The "weight" of the suffixes is stored in pos[]. Note that in the initial steps of the algorithm there can be two suffixes with the same "weight", that means that the first 2^gap letter of both suffixes are the same. Suffixes of length 2^(gap+1) can be seen as the concatenation of two suffixes of length 2^gap. Having calculated the "weight" of the suffixes of length 2^gap, we can safely compare suffixes i and j of length 2^(gap+1) using the pairs (pos[i], pos[i + gap]) and (pos[j], pos[j + gap]). The comparison first compares pos[i] and pos[j], if are equal, then uses pos[i+gap] and pos[j+gap]. Note that if i+gap or j+gap are not valid suffixes then the shorter comes first.

    → Reply
»
10 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Is that hash mod 2^64? I thought that's known to break?

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

could anyone care to explain how the above LCP algorithm work please? much appreciated!

→ Reply