Привет всем! Хотел узнать за сколько (асимптотика) работает сортировка строк следующим образом?
int n;
vector< string > a(n);
sort(a.begin(), a.end());
Будем считать, что все строки имеют длину от 1 до 1e5 и сумма длин всех строк не превышает 2e5. 1 <= sumLen <= 2e5
Количество строк от 1 до 1е5. 1 <= n <= 1e5
P.S. Известно, что существует сортировка строк за время O(sumLen) и O(sumLen * k) памяти или
за время O(sumLen * log(K)) и O(sumLen) памяти с помощью бора, но хотелось бы
разобраться с более короткой версией (с точки зрения написания кода). Заранее Спасибо!
не подумав сказанная дичь...
Такая сортировка даст нам строку, образованную конкатенацией наших строк в одну, причем такая строка будет лексикографически минимальной, а нам нужно отношение наших строк между собой.
Контрпример:
b и ba : bba > bab, но b < baПожалуй ты прав)
O(sumLen * log(n)), и вот почему.Предположим сначала, что все строки имеют одинаковую длину
L, тогдаsumLen = n * L.std::sortделаетO(n * log(n))сравнений, каждое сравнение делается заO(L). Получается сортировка заO(nL log(n)) = O(sumLen log(n)).Если же длины строк разные, то получится даже меньше операций, так как при сравнении длинной строки с короткой на последние символы длинной мы никогда не посмотрим.
Что касается памяти, говорят, что стандартом это не ограничивается. На практике используемый алгоритм сортировки и, соответственно, потребление памяти зависят от входных данных, но здравый смысл подсказывает, что вряд ли реализации понадобится использовать больше памяти, чем на поддержание перестановки
O(n)итераторов или на стек рекурсии глубинойO(n).Допустим, у нас n - 2 строки длины 1 и две строки длины k. Сходу неочевидно, что мы не получим слишком много сравнений больших строк друг с другом. И, кажется, чтобы доказать, что это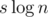
, нужно опираться на то, что сортировка в C++ применяется именно introsort.
Я тоже раньше этот факт только для Quick-Sort и модификаций доказывал... Забавно, вроде для MergeSort и HeapSort тоже верно. Интересно, есть хотя бы одна реальная nlogn сортировка, которая слишком долго сортит строки? =)
А что такое "реальная"? :)
По крайней мере не та, в которой стоит if на то, что если сортируемые элементы строки — то сортировать пузырьком :D
А если сортировка просто в конце делает O(n) сравнений последних двух элементов, чтобы убедиться, что они отсортированы, она реальная или уже нет? :)
В отличие от пузырька всё же она делает
сравнений всегда
Мы можем в любую nlogn сортировку вставить n сравнений первых двух элементов, от этого она останется nlogn и станет TL-иться на твоём примере. Но это искусственно созданная сортировка. Реальная -- в смысле, не искусственно испорченная, и за nlogn.
Можно сортирвку за
O(N * logN * logM). N — кол-во строк, M — длина макс. строки. Считаем хэш всех строк, и когда сравниваем 2 строки, используем бинпоиск. То есть общий префикс будет иметь равный хэш, а вот следующий символ будет отличаться.