is here! Finally, solutions can be spoilered!
For example, my solution to F from Чемпионат КРОК 2016 - Отборочный Раунд:

The first observation is that for a fixed set of species, the max. number of farms is the GCD of their a_i (we can say c_j=a_{N+j}). So we want the sum of GCDs over all K-element subsets.
The second observation is that this sum for the first x+1 species = sum for the first x species + number of K-1-element subsets containing the x-th species. In order to recalculate it, we only need to find out the number of K-1-element subsets such that their numbers and a_x have GCD equal to g for each divisors g of a_x (obviously, that GCD can't be a non-divisor of a_x); let's call the number of such subsets for given x p(g), then the answer in step x+1 = answer in step x + sum gp(g).
It's much easier to calculate the number of K-1-element subsets whose GCD is a multiple of g; let's call that number P(g). We'll get to that later, it's more important to show how to get p-s from P-s.
We'll calculate p-s in the order of decreasing g. At first, let's take p(g)=P(g); we need to subtract the subsets whose GCD is strictly bigger than g and a multiple of g. Since we calculated p(g') for all g' > g already, we can just subtract all p(g') such that g' > g is a multiple of g. However, we need to list divisors for all numbers anyway, so it's simpler to subtract p(g') from all p-s of proper divisors of g' right after calculating it.
The time complexity of this is O(number of pairs g | g' | a_x). The maximum number of such pairs can be found easily if we know divisor lists; it's 8505 for a_x <= 10^6. We don't need any modulos there, so that's manageable.
Now to computing P(g). If there are M_g species with numbers divisible by g, then P(g)={M_g over K-1}. Since M <= N+Q, we can precompute factorials and their modular inverses, which allows us to compute P(g) in O(1) time.
Computing M_g is very similar to p-s from P-s: when the number of species with f flowers (an analogy of P) increases by 1, M_d for all d|f (which is an analogy of p) increases by 1.
We also need divisor lists; for them, we can use a simplified sieve of Erathostenes. There are O(Alog{A}) divisors, where A=10^6 and the maximum number of divisors of one number <= A is D ~ 300, which means the total time complexity is O((N+Q)(D+8500)+Alog{A}), where the constant next to D is larger than the one next to 8500 due to modulos and more stuff to compute.
This may be too slow; to speed it up, we can use the fact that we don't need online processing for the first N added flowers.
UPD: Hell yeah, finals! I'll just leave this here.











Mathafaka!
I like it!
my solution is also O(M*8505) but it got TLE on pretest #7 :(
constant optimizations sucks, and all problems that have TL more than 3 seconds sucks too
We did not intend for any solution with the constant 8500 to pass. We tried to fail these. The intended solution is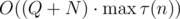 , where
, where 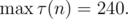
I'm amazed that C++ runs so quickly that taking a constant of 8500 passes. Maybe we should have made Q = 2·105, and N = 0 instead.
Our solution will be posted soon.
But how would you fail 8.5e8 subtractions?
Not sure, I was just noting that letting this pass was unintended... the constant factor on the other solution was high enough that I think anything substantially less than 8s was too little.
It doesn't really matter I guess, you should try finding a slightly faster solution anyways. :P
My solution works 2s without any optimisations. May be 4s time limit will be ok if you add all maxtests in pretests.
Auto comment: topic has been updated by Xellos (previous revision, new revision, compare).
it seems that you need to try out to be a victim of some terrorist attacks in order to understand why refugees are coming to your country.
instead of offending refugees, why not start to offend countries which are supporting terrorism because if those countries wasn't supporting terrorism there would not be refugees now.
I'd like to not turn CF comments into political discussion, thank you. We can continue by PM, though.
Then why you posted that video to public CF?
He probably doesn't realize honestly that its hurtful to some. I think he didn't mean to offend refugees. I think it was an ill-tasted jest.
Take a joke will ya? This is satire.
I don't think its easy for Syrians and other refugees to take these satires in good spirit. The rest of the world needs to understand that.
I'm Syrian.
You're not the only Syrian and you're not the only refugee(if you are a refugee at all) :)
My point is, its hard for someone who has lost someone very close in a war, or lost their homes, family and such, or just a general patriotic sentiment against war and how people are rendered homeless. Good to know you are still able to take a joke :) It means you haven't lost anything in other peoples' stupid wars.
I had 2 family members who were fighting in this war. One of them is dead, the other one still is.
Syrians like Jaddouh don't take jokes not because of the specific horrible situation, but because of the sensitivity culture where emotions are valued more than facts. I can go into more detail but this isn't the place for it. I just want to say that people don't have the right to not to get offended.
Very sorry for your loss :(
Spoiler