648A - Наибольший подъем
Для решения данной задачи насчитаем высоту каждой горы и сохраним ее в массиве h[], где h[j] равно высоте j-й горы. Для этого обойдем заданную матрицу, и если элемент, стоящий в строке i и в столбце j (строки и столбцы 0-индексированы), равен звездочке, обновим высоту j-й горы: h[j] = max(h[j], n - i). Осталось просто проитерироваться по столбцам от 0 до m — 2 включительно, и, если текущий столбец равен j, обновить величину максимального подъема или максимального спуска величиной |h[j + 1] - h[j]|.
648B - Собери стол
Для решения данной задачи сначала посчитаем длину одной собранной ножки стола и сохраним ее в переменную len (len = sum / n, где sum — это суммарная длина всех частей, а n — количество ножек стола). Сохраним длины всех частей ножек в массив a[] и отсортируем его по возрастанию. Затем переберем части ножек переменной i от 0 до n - 1 включительно и будем выводить в ответ пары вида (a[i], len - a[i]).
648C - Путь Робота
Сначала найдем стартовую позицию Робота, сохраним ее и присвоим значение стартовой позиции звездоке. Так как по условию задана ломаная без самопересечений и самокасаний верен следующий алгоритм: если есть соседняя с текущей клетка, в которой стоит звездочка, перейдем в соседнюю клетку, значение которой равно звездочке, и присвоим ее значение точке (при этом выведем букву, соответствующую направлению, в котором мы перешли). При этом соседняя клетка должна быть отлична от той, из которой мы пришли в текущую клетку. Если нет соседней клетки с звездочкой, значит мы обошли всю ломаную и нужно закончить работу программы.
648D - Собачки и миски
Если представить каждую миску в виде отрезка [uj - tj, uj + tj], то i-я собачка сможет покушать из j миски, если uj - tj ≤ xi ≤ uj + tj.
Будем решать задачу жадно. Рассмотрим самую левую собачку и те миски из которых она может покушать. Если таких мисок нет, то собачка не сможет покушать. В противном случае из мисок доступных самой левой собачке выберем для неё миску с самым левым правым концом. Далее не будем рассматривать эту собачку и эту миску и продолжим аналогично наши рассуждения.
Легко видеть, что такая жадность приводит к оптимальному ответу:
- Если самая левая собачка может покушать, то нет смысла ей не кушать, поскольку этим мы убираем одну миску и ухудшим ответ на единицу;
- Рассмотрим те миски из которых может покушать самая левая собачка. Все эти миски будут доступны и остальным собачкам кроме тех у которых правая граница находится слишком далеко влево. Таким образом, если мы хотим взять какую-либо миску (а мы уже поняли из пункта 1, что это стоит сделать), то выгоднее будет взять миску с самым левым правым концом, так мы не ухудшим выбор для собачек справа.
По этой задаче можно было попробовать написать другие жадности, но многие являются неправильными.
Для того, чтобы это реализовать отсортируем собачек и миски (по левому концу) слева направо. Будем идти слева-направо обрабатывая события появилась миска (в этом случае добавим её правый конец в какую-нибудь структуру данных) и появилась собачка (нужно для собачки в структуре данных найти самый левый подходящий правый конец).
Сложность: O(nlogn) или O(n) в зависимости от структуры данных (*set* или queue).
648E - Собери число
Заметим, что при построении ответа нам в любой момент важен только лишь остаток от деления текущего его префикса на k. Действительно, если текущий префикс ответа имеет остаток от деления на k, равный r, то при приписывании к префиксу числа ai этот остаток станет равный остатку от деления на k числа r·10li + ai (li — количество цифр в записи числа ai).
Тогда, очевидно, нас интересует получать любой остаток от деления такой операцией, используя минимальное количество цифр в записи. Конечно, остаток 0 мы можем получить сразу, используя пустой префикс, поэтому для остатка 0 нас будет интересовать второй по величине ответ.
Все описанное выше позволяет нам построить граф на k вершинах (от 0 до k - 1, соответственно остаткам), ребра в котором определяются числами ai: из вершины v в вершину 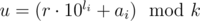 длины li, означающее, что с помощью дописывания li цифр мы можем из префикса с остатком v получить префикс с остатком u. Легко заметить, что некоторые ai в этом графе будут соответствовать одним и тем же ребрам (сейчас их nk) — это числа с одинаковой длиной десятичной записи и остатком от деления на k, поэтому стоит оставить лишь уникальные по такому критерию числа (их будет не больше 10k), и тогда количество ребер не будет превышать 10k2.
длины li, означающее, что с помощью дописывания li цифр мы можем из префикса с остатком v получить префикс с остатком u. Легко заметить, что некоторые ai в этом графе будут соответствовать одним и тем же ребрам (сейчас их nk) — это числа с одинаковой длиной десятичной записи и остатком от деления на k, поэтому стоит оставить лишь уникальные по такому критерию числа (их будет не больше 10k), и тогда количество ребер не будет превышать 10k2.
Теперь все, что от нас требуется — найти длину кратчайшего непустого пути из вершины 0 в саму себя же в построенном графе. Чтобы избежать столь неприятной цикличности, давайте просто добавим дополнительную вершину k, имеющую те же исходящие ребра, что и вершина 0, считая, что такой остаток может иметь лишь пустой префикс. Теперь задача сводится к нахождению кратчайшего пути из вершины k в вершину 0, которую можно решить алгоритмом Дейкстры за O(k2). Однако, в силу специфичности задачи, решение алгоритмом Форда-Беллмана (с правильными отсечениями, конечно) так же проходит все тесты, хоть в теории и имеет столь большие O(k3).
Восстановление ответа в задаче довольно стандартно, за исключением хранения дополнительного числа для каждой вершины, образовавшего ребро, по которому был осуществлен нужный в кратчайшем ответе переход.















648B — Собери стол Совершенно не обязательно вычислять длину ножки. Достаточно отсортировать массив частей по возрастанию длины. Первому элементу массива будет соответствовать последний, второму — предпоследний, и т.д.
а на каком языке представлен пример решения задачи 648B — Собери стол?
c++