652A - Gabriel and Caterpillar
The problem was suggested by unprost.
Let's consider three cases.
h1 + 8a ≥ h2 — in this case the caterpillar will get the apple on the same day, so the answer is 0.
The first condition is false and a ≤ b — in this case the caterpillar will never get the apple, because it can't do that on the first day and after each night it will be lower than one day before.
If the first two conditions are false easy to see that the answer equals to
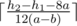 .
.
Also this problem can be solved by simple modelling, because the heights and speeds are small.
Complexity: O(1).
652B - z-sort
The problem was suggested by Smaug.
Easy to see that we can z-sort any array a. Let 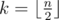 be the number of even positions in a. We can assign to those positions k maximal elements and distribute other n - k elements to odd positions. Obviously the resulting array is z-sorted.
be the number of even positions in a. We can assign to those positions k maximal elements and distribute other n - k elements to odd positions. Obviously the resulting array is z-sorted.
Complexity: O(nlogn).
652C - Foe Pairs
This is one of the problems suggested by Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A.
Let's precompute for each value x its position in permutation posx. It's easy to do in linear time. Consider some foe pair (a, b) (we may assume posa < posb). Let's store for each value a the leftmost position posb such that (a, b) is a foe pair. Denote that value as za. Now let's iterate over the array a from right to left and maintain the position rg of the maximal correct interval with the left end in the current position lf. To maintain the value rg we should simply take the minimum with the value z[lf]: rg = min(rg, z[lf]). And finally we should increment the answer by the value rg - lf + 1.
Complexity: O(n + m).
652D - Nested Segments
The problem was suggested by Alexey Dergunov dalex.
This problem is a standard two-dimensional problem that can be solved with one-dimensional data structure. In the same way a lot of other problems can be solved (for example the of finding the maximal weighted chain of points so that both coordinates of each point are greater than the coordinates of the predecessing point). Rewrite the problem formally: for each i we should count the number of indices j so that the following conditions are hold: ai < aj and bj < aj. Let's sort all segments by the left ends from right to left and maintain some data structure (Fenwick tree will be the best choice) with the right ends of the processed segments. To calculate the answer for the current segment we should simple take the prefix sum for the right end of the current segment.
So the condition ai < aj is hold by sorting and iterating over the segments from the right to the left (the first dimension of the problem). The condition bj < aj is hold by taking the prefix sum in data structure (the second dimension).
Complexity: O(nlogn).
652E - Pursuit For Artifacts
The problem was suggested by Alexey Dergunov dalex.
Edge biconnected component in an undirected graph is a maximal by inclusion set of vertices so that there are two edge disjoint paths between any pair of vertices. Consider the graph with biconnected components as vertices. Easy to see that it's a tree (if it contains some cycle then the whole cycle is a biconnected component). All edges are destroying when we passing over them so we can't returnto the same vertex (in the tree) after leaving it by some edge.
Consider the biconncted components that contains the vertices a and b. Let's denote them A and B. Statement: the answer is YES if and only if on the path in the tree from the vertex A to the vertex B there are an edge with an artifact or there are a biconnected component that contains some edge with an artifact. Easy to see that the statement is true: if there are such edge then we can pass over it in the tree on the path from A to B or we can pass over it in biconnected component. The converse also easy to check.
Here is one of the ways to find edge biconnected components:
Let's orient all edges to direction that depth first search passed it for the first time.
Let's find in new directed graph strongly connected components.
Statement: the strongly connected components in the new graph coincide with the biconnected components in old undirected graph.
Also you can notice that the edges in tree is the bridges of the graph (bridges in terms of graph theory). So you can simply find the edges in the graph.
Complexity: O(n + m).
652F - Ants on a Circle
The problem was suggested by Lewin Gan Lewin.
The first observation: if all the ants are indistinguishable we can consider that there are no collisions and all the ants are passing one through another. So we can easily determine the final positions of all the ants, but we can't say which ant will be in which position.
The second observation: the relative order of the ants will be the same all the time.
So to solve the problem we should only find the position of one ant after t seconds.
Let's solve that problem in the following way:
Consider the positions of all the ants after m time units. Easy to see that by the first observation all the positions of the ants will left the same, but the order will be different (we will have some cyclic shift of the ants). If we find that cyclic shift sh we can apply it
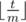 times.
times.After that we will have only t ± od m time units.
So the problem now is to model the process for the one ant with m and r ± od m time units. Note that in that time interval the fixed ant will have no more than two collisions with each other ant. So if we model the process with ignoring all collisions except the ones that include the fixed ant, we will have no more than 2n collisions.
Let's model that process with two queues for the ants going to the left and to the right. Each time we should take the first ant in the queue with opposite direction, process the collision and add that ant to the end of the other queue.
Hint: you will have a problem when the fixed ant can be in two different positions at the end, but it's easy to fix with doing the same with the next ant.
Complexity: O(nlogn).











Hello,
A) Thx for contest .. I loved the problem-set :)
B) I see one of the complexities in Russian in English version [problem 'D'] : "Сложность"
Hi Edvard
About C In such a situation: arr: [2, 4, 3, 1] Foe = (2,1), (3,4)
z[0]: {3}z[1]: {2}Your solution will work like this :
Initially, ans = 0, rg = 3ans += 3 , (i=0, rg = 3)ans += 1 , (i=1, rg = 2)ans += 0 , (i=2, rg = 2)ans +=-1 , (i=3, rg = 2)So your answer is = 3
but clearly the answer is 6
In arr: ((2,2), (4,4), (3,3), (1,1), (2,4), (3,1))
In index: ((2,2), (4,4), (3,3), (1,1), (0,1), (2,3))
Please tell me if I am missing something.
I think that's because author is using very many redefinitions.
Please check the code of the solution. The solution will be more clear for you after that.
Hi Edvard
I am quoting the code in the solution. As per the code you shared the solution for this example is 3: arr: [2, 4, 3, 1] Foe = (2,1), (3,4)
But there are 6 intervals. So either the code is not correct or I am missing something. Please do have a look.
Thanks
In the outer for-loop ,loop variable 'i' is decreasing (from n to 1 ,written as 'nfor' ).
Solution to problem E please!
For the time being, W4ynebot wrote a solution in the announcement blog, you can read it.
Hello everyone . Can someone please Help me in solving Problem A? I have seen several Solution . But failed to understand .
Can Anyone please Help ??
Let's say we have this input data:
This means that at 2 PM there is an apple on the tree at height of 90 cm, and at 10 cm height sits the caterpillar. We know, that between 10 AM and 10 PM caterpillar goes higher 4 cm/hour. When it's 10 PM caterpillar goes to sleep and slips down 1 cm/hour, until it's 10 AM again. So we have the process:
In our case caterpillars movements are:
In the middle of the 2-nd day the caterpillar is high enough to reach the apple, so the answer is 2.
"sleeping" ?? :D Sorry for nitpicking. You clearly meant "slipping".
He slips while sleeps :D
Oh yeah, you mentioned! I surely ruined the fun out of it! ;) By the way, were you the author of this problem? (I can't find the author information for any particular problem! :| )
I've suggested this problem and Edvard prepared it
And who invented the story?
I'm sure you can guess :D
Genius Simply .. I like the Statement & Way of your Derivation .
I thought that since the boy's school is closed at 2 pm, so he sees the caterpillar first at height h1 at 2 pm . So, the caterpillar should be at 10 cm height at 2 pm . I think a little more careful problem statement was required in A .
Any thoughts on problem F?
You need to make a couple of observations:
The final complexity is .
.
Hopefully that made some sense, it should be enough to solve the problem. Here's my solution by the way: 16961705
EDIT: Here's an even shorter solution: 16970841. Very simple compared to the one in the editorial :)
Actually it can be solved without any simulation. Time still will be O(n ln n) due to sort.
Very nice! It looks that W4yneb0t implemented that solution.
I had troubles understanding this. Could you give a more detailed proof on why this works please?
Which part needs explanation?
I don't understand why this would work. How come ((S*T)mod(N*M)-O)/M = answer.
See some formulas below.
Can you explain why "p_1 is equal to q_(1+offset)" ?
It's not equal, it means that ant from position p1 will move to position q1 + offset. Here is a proof:
Let ant from position p1 finishes at position q1 + t. Then ant from p2 moves to q2 + t etc. Then total (oriented) movement (total oriented distance traveled by ants) equals
(last t summands have +m because ant will go full circle before arriving to that position). On the other hand it equals S·t. So t = (St - O) / m.
I don't really understand this idea, could you explain why you add m. Isn't everything already mod m, why would it matter?
Edit: actually I am more confused now why the left hand side is equivalent to S*t.
Positions are mod m in a sense, but e.g. speeds aren't.
Left side is S*t because it's total oriented movement. So on the one hand it's speed multiplied by time, on the other — difference between finish and start positions.
But the offset doesn't seem like enough, for example a single ant can go around the circle many more than 1 time but this doesn't seem to be accounted for in the total oriented movement.
Another solution without simulation:
First, relabel the ants such that they are in increasing position with respect to their indices. We can reverse this relabelling at the end.
Next, imagine that each ant has a sign. When two ants pass each other they exchange signs. Consider the first ant (assume he is going right) — we know where it will eventually end up but we do not know what sign it will hold. Notice however that when the first ant meets another ant, the sign the first ant holds will increase by one. So we simply sum up how many times the first ant meets another ant.
Nsqrt(N) giving TLE in problem D :(
Nsqrt(N) = 1e9 for max test.
no N = 2e5 so NsqrtN ~ 1e8
yeah my bad
Hello,
I got question!
here I made two submitions of problem "D"
Accepted and TLE
The only difference in between them is "map" and "unordered_map" (One of them got TLE second Accepted (TLE with unordered_map))
it was hacked by this generator:
Anyway when I executed it in locale, the unordered_map is faster.
Can somebody please explain the magic behind this? :) Thx
I was also hacked by this generator, but solution with unordered_map took ~7s and solution with map took ~0.38s on my machine.
Hmm interesting ... I have "0m0.370s" for hash map and "0m0.583s" for map :/
interesting :)
Did you decrease the maximum load factor of the unordered_map when testing on your machine? Doing so makes the code faster and even acceptable.
I'm sorry, I'm afraid I don't understand, what "load factor" means
I just generated exact input and run it with "g++ -Wall -pedantic -Wno-long-long -std=c++11" (with the codes from above :/ )
You can check it out here. Since you didn't do it, it's pretty interesting that the solution with unordered_map ran faster on your machine.
Oh, didn't know about this ~ Thx! :)
Visual Studio STL is different from GCC STL (aka libstdc++). For example, the following code
prints 100001 for GNU G++/GNU G++11 and 1680716807 for Microsoft Visual C++ 2010. Also, unordered_set and unordered_map implementations themselves are probably different. So different STLs require different anti-hash tests. I guess that you are testing your program with Visual Studio while my anti-hash test is designed for gcc STL.
Nope, I tested under GCC STL (I think 4.7 version — if it can influence anything?)
anyway interesting (nice hack btw — didn't even know about the possibility ^_^ )
std::cout << std::hash()(N) << std::endl; returns same numbers as are arguments :O is it right?
Thx man and have nice day!!
Well, if my test doesn't cause slowdown, gcc version must influence something. There are nothing else to blame.
Yes (for gcc STL).
It's also possible to solve the problem B in O(n).
Code: 16934709
I believe this exact same problem exists in codechef's ex Easy section! And I did it the same way!
Can we use MO's Algorithm for solving D ?
complexity seems good. but I tried it and I got TimeLimit
I don't know why ? can anyone help me. tanx
I use too and I got TLE ;/
http://www.codeforces.com/contest/652/submission/17020791 using Mo's
thanks! :)
Here's my solution to Problem E: 16955949
As explained in the editorial, we are interested in all Edge-Biconnected-Components on the path from a to b. Instead of building the EBCC-tree, we can easily obtain all vertices in these EBCCs by adding a new edge between a and b. Since it was given that there is a path between every pair of vertices, there are now two paths between a and b, and hence, they are in the same EBCC. Furthermore, all EBCCs in the original EBCC-tree will be contracted to a single component.
To find this EBCC, I used our normal code to find bridges and biconnected components, together with Union-Find. For every edge that is not a bridge, I merge the two (components) of the endpoints of the edge. Afterwards, I merge the components of a and b separately, because the algorithm fails when there is only a single edge between a and b.
Next, for every edge with an artifact, I check whether both endpoints of the edge belong to the component of a and b (using the Union-Find datastructure we built earlier). If there is such an edge, the answer is 'YES'. Otherwise, print 'NO'.
All together, this solutions requires almost no code apart from reading the input, the Union-Find and Biconnected Components algorithm.
Really brilliant idea to add edge from a-b to make they are in same EBCC.
btw, if you can find EBCC correctly for multigraph, then only needed work is for any artifacts (u, v) check u.bcc == a.bcc and v.bcc == a.bcc.
Here is my code: click
In the code, used 'metParent' variable to handle multigraph(so if u — v have multiple edges, then do not classify as bridge)
Can anyone please explain C using two pointers..I have been trying for 2 days but all my efforts are in vain.....Please???????????????
In a sorted array work this rules:
So you sort the array, and then build a new one using pair of pointers
(1, n)or(1, mid)making one of this sequences:The first one is simpler to implement, considering the case where n is odd
Thanks for the quick tutorial. Can you please tag the contest to this tutorial?
Done.
I think there are typos in the explanation of problem A:
In point 2, it should be
a<=binstead ofa>b.In point 3, it should be
ceil((h2-h1-8*a)/(12*(a-b)))instead ofceil((h2-h1)/(12*(a-b))).Thanks. Fixed.
Shouldn't the complexity of C be at least O(n log n) . See these two for loops :
nfor(i, n) { forn(j, sz(z[i])) rg = min(rg, z[i][j]); ans += rg - i; }Can anyone please explain a little bit ?The total size of all z[i] is O(m). I've fixed the complexity from O(n) to O(n + m).
BTW, problems were really nice . Just A's problem statement was tough to understand.
How is the complexity O(n+m) ? If all the z[i]'s contains elements in decreasing order , then the second 'for' loop will have a complexity O(n) .
z[0] + z[1] + ... + z[n — 1] = m
In Problem E How to solve if changing the route which originally (a to b) to (a to b then back to a)? Thanks!
Hi, Can anyone explain the editorial for problem D? I am unable to understand the use of Fenwick Tree for this particular problem. Also I am not sure but there seem to to be some typos in the editorial i.e bj<aj instead of bj<bi in fourth line and bj < bj instead of bj<bi in second last line. Please correct me if I am wrong?
Good day to you,
let's say you have an array (later Fenwinck → complexity) and for every END of segment, you add 1 to the value (I mean => if you have segment [1,5], then you do Array[5]++)
PS: A necessary here is to make the values lesser (but preserve their order). So from [1,10000000],[3,50000], you would do [1,4][2,3] (otherwise you would not have enough memory for it)
Now let us sort the array of segments by their beginning.
Here, for every segment you do following operation:
I) Sum all values of all elements of array, from 0 to END
II) Substract END of this segment from array (so for [1,5] you would do Array[5]--)
Now see, what happened to all segments. The sum of values is the number of ends, which end earlier, than END of current segment. How can we be sure that we didn't include any extra segment? Well it is thanks to (II). Here we already substracted values of ALL segments, which begin earlier, then our current segment (so we are considering only points which begin later and we are searching for those, whose END is earlier, than current END).
Here you see, that the complexity is O(N^2). It is time to use Fenwick. It has exact property we want! Add/Substract a value of any one element (in logarithmic time) + get the sum of 0→END also in logarithmic time!
If the explanation was confusing, or not enough, do not hesitate and ask for additional questions :)
Good Luck man! ^_^
Thanks man. I got the idea.
How to know when to use Fenwick tree ?
I have an alternate solution to F (maybe it's already in the editorial if I didn't read it properly).
Like in the editorial, we reduce the problem to finding the location of a single ant after x time units.
We plot the lines for each of the ants on the Cartesian plane, and "repeat" them with period m so that we have all the necessary lines. By necessary, I don't mean all infinity lines, because we only care about and will only query for up to m time units. This means that for the second sample input:
The lines for the ant
5 Larey=-x-3,y=-x+5andy=-x+13. All other lines are irrelevant, because we can never reach them.Now, notice that for any ant, it follows a path on the lines, and each time it reaches an intersection, it swaps — it jumps to another line. We can observe that this means that if the ant starts at the k-th lowest line, it always stays on the k-th lowest line.
So since we have all necessary lines, we can find the value of k, and then find the k-th lowest y-coordinate to find the final location of the ant.
We can use this algorithm to find the cyclic shift per period, as well as the final movement of the ant.
Accepted solution: 17126112
I am trying to understand the complexity of the below submission for problem E (Its a nicely written code, btw).
http://mirror.codeforces.com/contest/652/submission/16927126
Especially the below line in
dfsThe
findmethod takesO(N). How to prove that the overall solution will not haveO(N^2)for some worst case scenario?Hi! I wanted to share my solution for the problem D, using order statistics tree (see this article for more info about the data structure): My solution
dalex could not understand your solution for problem D. Please explain.
Try this:
My solution is available in my last submits.
For problem E Pursuit for Artifacts, is it always possible to have a path from A to B passing some artifact edge E if all of them are in same biconnected component?
It's true, but it's not that easy to be proved. Every biconnected graph can be constructed as follows: first we have a loop, and each time we add a path on it. We choose a loop that contains an artifact edge E, then we can construct a path passing the edge E, by moving vertex A and vertex B to older paths or loop in the structure above.
Yes. Let (u,v) be the artifact edge. Suppose for every path p1 from A to u and p2 from B to v inside the component p1 and p2 have common edges. You can see that there exists a certain edge e* in the component for which every such pair of paths p1' and p2' pass through, otherwise you can construct disjoint paths. This edge e* separates the biconnected component in two which leads to a contradiction.
In problem E, what is the proof that if a single bi-connected component (let's call it $$$A$$$) has a 1-edge, then you one can go from any point in $$$A$$$ to any other point in $$$A$$$ that travels this 1-edge and never visits the same edge twice?