→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
34:34:38
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
34:34:38
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 07:00:23 (l3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










registration started , register soon since number of people allowed to participate are limited(2500)
Is it a rated contest?
What is the idea of 1000!!!
Greedy approach is ok, try the least index to go now and check whether it is possible to finish process from current state.
To check it one can prove that it is optimal to go to the deepest node from current one every time.
Could not understand, what should be done in case of walking to the least index from current state doesn't brings to finish?
Try the next unvisited least index or something else? If try the next — it's looks like bruteforce.
We pick node with the least index and trying to find some answer(maybe not optimal one). If we can find it, we take this node to answer and trying to make next move, or try to pick node with greater index and so on.
Still could not understand.. How to do it? Dirac's theorem about hamiltonian path or something else?
To check if answer exists, every time we should go to the deepest node which is reachable from current one.
Is there any way to solve 1000 in O(N3)?
Yep.
Let's do the following process: suppose we have a function that is able to, given a sequence of already visited vertices (we are staying at the last vertex of that sequence), tell if this sequence can be extended to a correct permutation. Having such function, we can determine the answer in O(n2) calls of it by restoring the elements of the desired permutation one by one.
Now we need to implement such function. This can be done via pretty easy DP, smth like D[v] = minimum number of vertices above v we should visit in order to visit all vertices in the subtree of v. It can be calculated in O(n).
If you can check if there exists a sequence starting with a1, a2, ... in O(N) then you can solve the question in O(N^3).
To do this: we remove all the vertices in the sequence that we already decided to use from the tree: so if we decide to go to 2, then all of 2's children are now children of 2's parents, etc. Now we can perform a tree dp[], taking special consideration of which is the last a_i we decided to use.
dp is number of times you need to leave the subtree.
Could you please provide a link to your source code here?
It would be helpful for me to understand the solution.
Interestingly enough there is even an O(N^2) solution. The main idea is that you can find nodes that are "good to go to" without breaking the traversal of the tree in O(N). If you are interested you can see my code in the practice rooms. As a problem setter I decided to not give it with N <= 1000 xD
Not related to problem.
I am getting the above error. I tried reinstalling java, using javaws to run it from command line, downloading the applet again.
There is one solution where I have to add the site as exception list in java. But I don't know the exact site address of topcoder. If someone knows please help.
I had the same problem and resolved it using your solution: added "http://www.topcoder.com" to the list of exceptions.
I tried that too and same problem.
Ohh found the mistake, instead of http://www.topcoder.com I have written http://topcoder.com bad habit of using browser.
Adding "http://www.topcoder.com" creates this message:
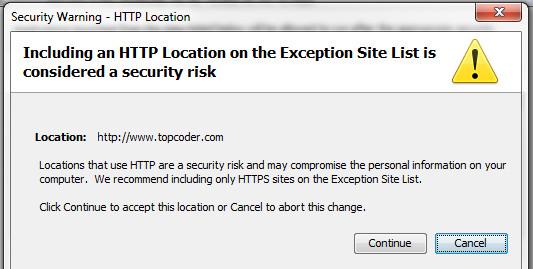
so, I added this: "https://www.topcoder.com" but didn't work!
click "continue" after this and it works !
i had the same problem. and i solved it finding the "java control panel".
There you choose the sequrity tab and set it to medium .
I think allowing medium would be riskier for other application. We actually trust topcoder that's why added it as exception :)
I had the same issue and decided to try web applet, in my opinion it worked fine but it was difficult to find things like how enter to the contest, open a problem, test a code, and finally I couldn't find how to see the global ranking.
Thank you! Now I can write 1001 reasons to hate the Arena! I only had 1000 till date!
it is in binary right!!
can anybody please explain div-2 500 by binary search and DP ??
Suppose you have another problem, you have an array A and an integer D, what is the maximum number of disjoint pairs you can form where a pair(x, y) can be formed if abs(A[x] — A[y]) <= D, this can be solved by dynamic programming in O(N^2).
In the original problem we can binary search D.