Can anyone give me an idea how to solve this problem ? Tour de Byteotia Thanks in advance!
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/23/2024 02:51:50 (i2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Auto comment: topic has been updated by saba_tavdgiridze (previous revision, new revision, compare).
Am I right or it is enough to find any spanning tree and delete other edges?
Apart from that, POIs have editorials. Try searching oi.edu.pl website
You're wrong since the graph is not necessarily connected, hence it can have no spanning tree.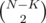 is possible.
is possible.
By the way, even if the input graph always had a spanning tree, the solution would be still wrong.
Simply consider a clique, where you would add N - 1 edges and at least
Let's try to add the maximum amount of edges so that no cycle passes through vertices 1..K.
You can first of all add all "safe" edges (x; y) — those which have x>K and y>K.
After that, iterate through the others, and add an edge only in case it won't form a cycle (this can be checked with the help of DSU).
After we're done, the answer is formed by the edges we didn't add.