UPD: I found a blog describing this blog: Link.
Hi!
Most of the people know about dsu but what is the "dsu on tree"?
In Iran, we call this technique "Guni" (the word means "sack" in English), instead of "dsu on tree".
I will explain it and post ends with several problems in CF that can be solved by this technique.
What is the dsu on tree?
With dsu on tree we can answer queries of this type:
How many vertices in the subtree of vertex v has some property in 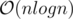 time (for all of the queries)?
time (for all of the queries)?
For example:
Given a tree, every vertex has color. Query is how many vertices in subtree of vertex v are colored with color c?
Let's see how we can solve this problem and similar problems.
First, we have to calculate the size of the subtree of every vertice. It can be done with simple dfs:
int sz[maxn];
void getsz(int v, int p){
sz[v] = 1; // every vertex has itself in its subtree
for(auto u : g[v])
if(u != p){
getsz(u, v);
sz[v] += sz[u]; // add size of child u to its parent(v)
}
}
Now we have the size of the subtree of vertex v in sz[v].
The naive method for solving that problem is this code(that works in O(N ^ 2) time)
int cnt[maxn];
void add(int v, int p, int x){
cnt[ col[v] ] += x;
for(auto u: g[v])
if(u != p)
add(u, v, x)
}
void dfs(int v, int p){
add(v, p, 1);
//now cnt[c] is the number of vertices in subtree of vertex v that has color c. You can answer the queries easily.
add(v, p, -1);
for(auto u : g[v])
if(u != p)
dfs(u, v);
}
Now, how to improve it? There are several styles of coding for this technique.
1. easy to code but  .
.
map<int, int> *cnt[maxn];
void dfs(int v, int p){
int mx = -1, bigChild = -1;
for(auto u : g[v])
if(u != p){
dfs(u, v);
if(sz[u] > mx)
mx = sz[u], bigChild = u;
}
if(bigChild != -1)
cnt[v] = cnt[bigChild];
else
cnt[v] = new map<int, int> ();
(*cnt[v])[ col[v] ] ++;
for(auto u : g[v])
if(u != p && u != bigChild){
for(auto x : *cnt[u])
(*cnt[v])[x.first] += x.second;
}
//now (*cnt[v])[c] is the number of vertices in subtree of vertex v that has color c. You can answer the queries easily.
}
2. easy to code and  .
.
vector<int> *vec[maxn];
int cnt[maxn];
void dfs(int v, int p, bool keep){
int mx = -1, bigChild = -1;
for(auto u : g[v])
if(u != p && sz[u] > mx)
mx = sz[u], bigChild = u;
for(auto u : g[v])
if(u != p && u != bigChild)
dfs(u, v, 0);
if(bigChild != -1)
dfs(bigChild, v, 1), vec[v] = vec[bigChild];
else
vec[v] = new vector<int> ();
vec[v]->push_back(v);
cnt[ col[v] ]++;
for(auto u : g[v])
if(u != p && u != bigChild)
for(auto x : *vec[u]){
cnt[ col[x] ]++;
vec[v] -> push_back(x);
}
//now cnt[c] is the number of vertices in subtree of vertex v that has color c.
// note that in this step *vec[v] contains all of the subtree of vertex v.
if(keep == 0)
for(auto u : *vec[v])
cnt[ col[u] ]--;
}
3. heavy-light decomposition style  .
.
int cnt[maxn];
bool big[maxn];
void add(int v, int p, int x){
cnt[ col[v] ] += x;
for(auto u: g[v])
if(u != p && !big[u])
add(u, v, x)
}
void dfs(int v, int p, bool keep){
int mx = -1, bigChild = -1;
for(auto u : g[v])
if(u != p && sz[u] > mx)
mx = sz[u], bigChild = u;
for(auto u : g[v])
if(u != p && u != bigChild)
dfs(u, v, 0); // run a dfs on small childs and clear them from cnt
if(bigChild != -1)
dfs(bigChild, v, 1), big[bigChild] = 1; // bigChild marked as big and not cleared from cnt
add(v, p, 1);
//now cnt[c] is the number of vertices in subtree of vertex v that has color c. You can answer the queries easily.
if(bigChild != -1)
big[bigChild] = 0;
if(keep == 0)
add(v, p, -1);
}
4. My invented style  .
.
This implementation for "Dsu on tree" technique is new and invented by me. This implementation is easier to code than others. Let st[v] dfs starting time of vertex v, ft[v] be it's finishing time and ver[time] is the vertex which it's starting time is equal to time.
int cnt[maxn];
void dfs(int v, int p, bool keep){
int mx = -1, bigChild = -1;
for(auto u : g[v])
if(u != p && sz[u] > mx)
mx = sz[u], bigChild = u;
for(auto u : g[v])
if(u != p && u != bigChild)
dfs(u, v, 0); // run a dfs on small childs and clear them from cnt
if(bigChild != -1)
dfs(bigChild, v, 1); // bigChild marked as big and not cleared from cnt
for(auto u : g[v])
if(u != p && u != bigChild)
for(int p = st[u]; p < ft[u]; p++)
cnt[ col[ ver[p] ] ]++;
cnt[ col[v] ]++;
//now cnt[c] is the number of vertices in subtree of vertex v that has color c. You can answer the queries easily.
if(keep == 0)
for(int p = st[v]; p < ft[v]; p++)
cnt[ col[ ver[p] ] ]--;
}
But why it is  ? You know that why dsu has
? You know that why dsu has 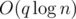 time (for q queries); the code uses the same method. Merge smaller to greater.
time (for q queries); the code uses the same method. Merge smaller to greater.
If you have heard heavy-light decomposition you will see that function add will go light edges only, because of this, code works in  time.
time.
Any problems of this type can be solved with same dfs function and just differs in add function.
Hmmm, this is what you want, problems that can be solved with this technique:
(List is sorted by difficulty and my code for each problem is given, my codes has heavy-light style)
600E - Lomsat gelral : heavy-light decomposition style : Link, easy style : Link. I think this is the easiest problem of this technique in CF and it's good to start coding with this problem.
570D - Tree Requests : 17961189 Thanks to Sora233; this problem is also good for start coding.
Sgu507 (SGU is unavailable, read the problem statements here) This problem is also good for the start.
HackerEarth, The Grass Type This problem is also good for start (See bhishma's comment below).
246E - Blood Cousins Return : 15409328
208E - Blood Cousins : 16897324
IOI 2011, Race (See SaYami's comment below).
291E - Tree-String Problem : See bhargav104's comment below.
1009F - Dominant Indices : 40332812 Arpa-Style. Thanks to Tanmoy_Datta.
343D - Water Tree : 15063078 Note that problem is not easy and my code doesn't use this technique (dsu on tree), but AmirAz 's solution to this problem uses this technique : 14904379.
375D - Tree and Queries : 15449102 Again note that problem is not easy :)).
716E - Digit Tree : 20776957 A hard problem. Also can be solved with centroid decomposition.
741D - Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths : 22796438 A hard problem. You must be very familiar with Dsu on tree to solve it.
For Persian users, there is another problem in Shaazzz contest round #4 (season 2016-2017) problem 3 that is a very hard problem with this technique.
If you have another problem with this tag, give me to complete the list :)).
And after all, special thanks from PrinceOfPersia who taught me this technique.











A2OJ's DSU Section has quite a few tree DSU problems.
Thank you for this post, it explains the theory well and is very easy to read.
بدك تضل تتمنيك عكل بوستات الخرا ؟
unlike this comment
What does the variable "keep" denote ?
The way I understand HLD here is basically if a child is the big child, we don't want to recompute answer for it to reduce computation. So we just store the answer for it in the
cntarray already so that it's parent doesn't need to re-dfs this subtree.keepdenotes whether or not this child is that big child. Please correct me if I'm wrong. :)Look at last two lines:
It means that if
keep == falseafterdfsclearvs subtree information fromcnt. And ifkeep == true, don't clearvs subtree information fromcnt. In other word ifkeep == trueafter callingdfs, for eachufrom subtree of verticev,col[u]is incnt(cnt[ col[u] ]++).And NibNalin is right.
keepistrueif and only ifvis biggest child of it's parent.Hi Arpa, thanks a ton for this awesome post. I have really learnt lot from it.
I do have one question though. What is the advantage of having keep=false? If that part is kept as it is, without clearing, doesnt the computation become faster? Can you please help clearing this doubt?
Hi, Thanks.
Consider vertex v has two children, q and p. If you call dfs for both of them with keep = true, they will mixed up their information, and queries will be incorrectly answered.
Observations to understand the complexity:
dfsfunction visits each node exactly once.n^2. Note that in theaddfunction, we only go down from a vertex to its children if the edge connecting the vertex to the child is a light edge.You can think of it in this way, each vertex
vwill be visited by a call to theaddfunction for any ancestor ofvthat is connected to a light edge. Since there are at mostlog(n)light edges going up from any vertex to the root, each vertex will be visited at mostlog(n)times.So the algorithm is: Say you are at a vertex
v, first you find the bigchild, then you run dfs on small childs, passing the value of keep as0. Why? So they are cleared from cnt. Then you run a dfs on bigchild, and you do not clear it fromcnt. Now,cntstores the results for all vertices in the subtree ofbigchild(since we clearedcntfor small childs and didn't do so for the bigchild), so we call theaddfunction to "add" the information of children of current vertex that are connected to it via a light edge. Now we are ready to compute the answerAs you said "add" function goes down using only light edges,Don't these two lines
if(bigChild != -1) big[bigChild] = 0;of heavy light decomposition implementation would affect it as if you call "add" after all dfs are done and returned to the root then we only have one heavy edge marked that of root itself others are zero so as "add" goes below it traverses whole tree. Help me here.Got it.
For those who had same doubt as I had: First lets understand why it is wrong to remove it,consider you are at particular node(let it be called A) in recursion,above line is not there,you have 3 children one of them is big child(3rd) while others are normal so you traversed inside 1st and came back to A then you traversed inside 2nd child if you do not have above line then while going inside this children you would have all answer for big children of 1st child which would mess your answer. Now let's understand why complexity is O(n(log(n)):
Note 1: To calculate complexity you need to measure how many times add function visits the ever y node.
Note 2: For first add called at a node: A node will visited by add only through its ancestors which are connected by light edges so n nodes log(n) light edges above it this gives us O(n(log(n)))
Note 3: For second add called at a node: Now somebody may protest that that after above mentioned line(big[bigChild]=0) we are unmarking heavy edge and also calling add after that which may mess up complexity as it travels every node below it which is O(n) but keep==0 condition ensures that for each node there atmost log(n) nodes above in ancestor which have keep=0 function is called.which again gives O(n(log(n)).
Giving us finally O(n(log(n))) complexity. Follow this link to understand heavy light decomposition's properties: https://blog.anudeep2011.com/heavy-light-decomposition/
In second easy with O(n*lg n)
Why if(keep==false) we delete only vertex from main vector
but we don't delete vertex from cnt which we changed here:
There was a mistake in writing. I'm sorry.
Thanks for reporting this problem.
code should be:
Instead of:
I have edited that.
can someone tell me how 208E is solved with this technique? thanks a lot.
You need to compute for each pair
v pthe p-th cousin of v. That is equivalent to finding the number of p-th descendants of the p-th ancestor ofv— 1.So for each query, replace
v pwithp_th_ancestor_of_v p. Now you need to store incntthe number of nodes at a certain depth. In other words,cnt[x]should be equal to number of nodes at depthxin the current subtree.Code for Reference: http://mirror.codeforces.com/contest/208/submission/17513471
can't understand why for every vertex v we ans[depth[v]] increase by 1 when we call add function,why must we do it?or why it must be ans[deth[v]] when depth[v] means distance from root to v?
ans[h]is equal to number of vertices with height h, (with distance h from root).Let par, p'th ancestor of v, the answer to query is:
Consider only subtree of vertice par, print ans[ height[v] ] — 1.
So with method above we can process all of the queries.
See my code for better understanding.
thanks everyone , now i understand.
If i haven't read this article, i wouldn't get ac on this problem. It is another problem which can be solved easily by dsu.
here is my code in HLD-style.
Thanks!
Thanks! Added to list ;)
I can't understand why the second code is correct...
Consider this example:
We wanna calculate the cnt for Vertex 8. These are the steps:
Going to Vertex 1
Going to Vertex 2 by keep=0
Going to Vertex 3 by keep=0,Vec[3]={3}
Going to Vertex 4 by keep=1,Vec[4]={4},Cnt[color[4]]=1
Going back to Vertex 2,Vec[2]={2,4},Cnt[color[4]]=0,Cnt[color[3]]=1
And then when we go to Vertices 5,6,7,8 still Cnt[color[3]]=1.
Also sorry if I did the steps wrong...
UPD Thank you for editing the blog. My problem fixed.
Great post. If you explained the idea before showing the code, it would be better to understand. Also commenting the variables meaning in the code would be of great help.
It would be good to mention that most solutions will answer the queries offline, which may be a problem sometime (maybe someone didn't notice this lol).
Also, it would be nice to post hints about the solutions.
Proving explicitly why it is nlogn would be good too (ie. as each node's subtree set gets merged into one set of size equal or greater, and the base set has size 1 and the last set has size n, then we take logn steps to go from 1 to n. Summarizing, each node gets merged logn times, so the total complexity is O(nlogn)).
Here's my solution to 343D, maybe it will be of help to someone: 18958875. A lot easier to code than the one in the tutorial.
Thanks for your suggestions first !
I proved that it is O(nlogn) : You know that why dsu has O(q log n) time (for q queries); the code uses same method. Merge smaller to greater.
And about your code (18958875), anyone has a different opinion !
Thanks for the reply!
Yeah, you did prove. People who remember DSU's proof will most likely understand. I stated a more extensive proof would be better thinking about people who don't exactly know the proof. Don't take me wrong, but they may get a little confused reading this proof.
I mentioned my code exactly because everyone has a different opinion,. Maybe it'll help a later reader, that's all.
Sorry this might be a stupid question to bring up, but why is the complexity of the heavy-light decomposition style one in O(nlogn)?
In the case where each node has at most two children: Denote the root node of the tree as u, which is of size s. The child of u connected to the lighter edge is of size at most . So the total number of nodes on which we run the "add" function would be at most
. So the total number of nodes on which we run the "add" function would be at most 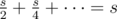 . So I don't understand where the log(n) factor comes from.
. So I don't understand where the log(n) factor comes from.
The online tutorial for HLD says a new chain is built when we arrive at a child node via a lighter edge, where each chain is stored as a segment tree, and so I can see there is indeed a O(logn) factor involved.
Regardless can you perhaps elaborate a little bit more on the time complexity of the dsu structure? Thank you!
Hi !
The online tutorial for HLD says a new chain is built when we arrive at a child node via a lighter edge, where each chain is stored as a segment tree, and so I can see there is indeed a O(logn) factor involved.
As you know, if you use
segment treeinheavy-light decomposition, each query time complexity will be O(log2(n)). Because in each query you will go O(log(n)) chains and in each chain it will spend O(log(n)) time.Now, I will proof that "heavy-light decomposition style implementation" of "dsu on tree" is O(n.log(n)):
Consider a complete binary tree with n vertices. In dfs function you will run another dfs function in child (T(n / 2) * 2) and you will call
addfunction and it will spend O(n / 2) time. So, T(n) = n / 2 + 2 * T(n / 2) = O(n.log(n))Pardon me , but I don't follow. Which dsu are you talking about? The one with inverse-Ackermann function?
No. Dsu with size compare. Like this :
In easy to code but O(nlog^ 2), I cant't understand why do we store the size of subtrees of vertices in array sz and use it as the criteria for choosing the big child, I think we should store in the array "sz" the number of distinct colors in the subtree of any node v, because that is what we actually iterate on when transferring the map from v to u, why is this wrong?
Hi !
It isn't wrong! Both of your method and mine have the same worst case. But your average is better.
Is child's subtree-size working as a heuristic for the number-of-distinct-colors in that child?
Ahh, thanks gabrielsimoes, for anyone struggling to understand: n*log^2n is about answering queries OFFLINE right during the dfs. After the dfs has finished the cnt[v] will no longer be a valid map for vertices that were chosen as bigChild.
http://mirror.codeforces.com/problemset/problem/291/E 291E - Древесно-строковая задача Arpa This problem can also be done by dsu on trees. Calculate hash value for each suffix value of target string. Then for each suffix of an edge if it is a valid prefix of the target string we would just need the frequency of the hash value of the remaining suffix of the target string in its subtree which can be maintained by this technique. The case when the entire string occurs in an edge can be dealt with separately.
Thanks added to list, but it can be solved very easier : 19827525, just use KMP.
Just use hashes :) http://mirror.codeforces.com/contest/291/submission/29431526
Hello Arpa,
The technique which you've used in this question, for the KMP solution, in which you've created the
nxt2D array, is it called something? Is it some recognized idea or did you just came with it on the go?Basically, you removed the inner while loop of KMP for matching strings. Instead of jumping multiple times to check whether the current characters match, you created a DP, using which we can do that in a single jump. That saves a lot of time, as we would have to do that for each string in the tree, while matching.
So, is this some already defined method?
Hello.
Do you know automata? I'm building automata from the string.
I do know automata. But damn. That's some beautiful automata you got there. GG.
Please send me a code of the solution with this techinque)
Here is bhargav104's solution
EDIT: Sorry. It doesn't use DSU on trees. Rather, it uses KMP.
Actually, in China, we call this method as "Heuristic Merge" which always merge the smaller to the bigger. Not hard to understand each vertex will be visited in O(log n) times because when we visited a vertex, then the size of tree which the vertex is in doubled.
Hey Arpa,
In your my invented style I'm unable to understand that why in third loop are you not checking for u not being parent of v. Why are you only checking for just u not being the big child.
Thanks in Advance
Sorry, fixed. It's because I've copied my code from 741D - Помеченное буквами дерево Arpa и забавные пути Mehrdad, input for this problem was a rooted tree.
Thanks a lot,
Also, I think there is one more mistake. You never added col[v] to the array. Am I missing something. Thanks in advance.
You are right, I'm very thankful to you. I was careless while coping the code from polygon.
In the easy to code O(nlogn) method
vec[v]stores all the vertices in the the subtree rooted at v . How will this fit into memory if we are not deleting the vec of child after merging it with the parentUsed memory is always less than or equal to time complexity, so when time complexity is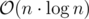 , used memory is less than or equal to
, used memory is less than or equal to 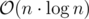 . In this case, used memory is
. In this case, used memory is 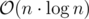 . Although if you delete useless vec's the memory become
. Although if you delete useless vec's the memory become 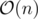 .
.
Thanks for the reply . I think this problem can also be solved using your approach. (The Grass Type HackerEarth)
I'll add this problem to the post if I find it related, I'm thankful anyway.
Edit : Note that this is not my approach, but I'm the first man who publishes a tutorial about this (not sure), Sack has been used in INOI, IOI and ACM several times, so it isn't a new thing, invented be me.
Edit : Added.
Can you mention probelms from the IOI that are solved with sack ?
I'll add one of them tonight.
Edit : Added.
Wow, I didn't think of solving it with sack.Thx
HEY Arpa i've solved all of the problem u mentioned above except digit tree, arpa's letter marked tree and ioi 2011 race.. Can you share a code for ioi 2011 race which uses sack.
Unfortunately, I don't have enough time.
Hi Arpa, I can not understand, why is this approach called dsu on tree? This approach has a nice trick to reduce complexity by saving data about "big child". I can't see any special similarity with general dsu approach. In general dsu problems, we merge 2 subset into 1 set by linked list approach. But, in your tutorial there is no "merge" function. Am I missing something?
Also I see that, in your 600E's solution 14554536 you used merge functon. I can't understand, could you please explain that code?
In fact we are merging information of small children with big child. Think more.
In that code, mrg function merges information in u into v.
Hi Arpa! Thanks for making this tutorial.
I just want to make sure my understanding is correct: this merging smaller maps into larger ones takes logarithmic time because when a vertex is merged, the new map it is in at least twice its size. Hence, merging can only happen log(n) times for each of the n vertices, leading to a total runtime of O(nlogn)?
Thanks!
Yes, but note that if you use map, it's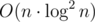 .
.
If you use unordered_map, does it become O(n·logn), then?
Unordered_map is theoretically O(n) per query. But you can suppose that it's O(1) per query in code.
Why do we need to iterate through the children of v after
add(v,p,-1)in the naive approach?dfs() solves the problem for all the nodes, not just one. So, after you've gotten the answer for v, it will calculate the answer for its children.
101 Hack 47 Summing Tree was solved using this technique by satyaki3794 Submission
also 778C - Петрович --- полиглот is solvable with a similar tecnique: is that DSU on tree?
yes
Can anyone give me a link to "Shaazzz contest round #4 (season 2016-2017) problem 3" or tell me where can I find it? Thanks.
It's a Persian contest.
Can you tell me where can I find it? I searched for it just now but didn't get it.
Link.
Thank you!
APIO 2016 Fireworks uses this, but is a much harder problem.
Arpa, in the Easy to code but O(nlog2n) section code you have written a commented line that is :
//now (*cnt)[c] is the number of vertices in subtree of vertex v that has color c. You can answer the queries easily.. But I think it would be//now (*cnt[v])[c] is the number of vertices in subtree of vertex v that has color c. You can answer the queries easily.. Will(*cnt)[c]changed with(*cnt[v])[c]?Hi. Thanks. Edited.
You can solve APIO 2012 Dispatching with this technique too.
IOI 2011 — Race What is the idea of DSU on tree for this problem? I know of a solution based on Centroid Decomposition.
keep map<distance from root, depth> for all subtrees. By merging them from smaller to larger, you can get O(nlog^2n) solution.
914E - Палиндромы в дереве can solve with sack too, Arpa :)
ps: for this problem centroid decompose works too... :)
can anyone please explain how to solve 716E using this technique?
In the contest 600, no one can view other's submissions except his own.
That's why no can see your submissions for 600E - Lomsat gelral except you.
So, please give alternating link of your solutions for the first problem in the list, 600E - Lomsat gelral
Hi.
Thanks for your feedback. Here it is: Link.
Thank you !
Another problem which can be solved by this technique: Coloring Tree
Its easier than 600E - Lomsat gelral.
One more : 932F - Сбежать через лист
No good explanation! Only code! Worst tutorial.
If you have a doubt why not ask in the comments rather than whining about how bad the tutorial is.
Nice tutorial!
and also happy Nowruz:)
Could you please explain 2no. style ? [Upd : Got it ]
In 2nd style Arpa can you please explain?..when we do cnt[u]=cnt[heavy child] does this happen in O(1)?
if yes -> how? else what the benefit of doing this? upd[got it]
For those who still confused about the time complexity, I found this explanation by radoslav11 helps a lot.
What is col[v]?
Color of the v-th vertex
I loved the way you used the Euler tour sequence to iterate through the subtrees. My 2 cents is a way to use C++ to implement this nicely. The main idea is to use a structure, that keeps pointers instead of
st[v]andft[v], and to give it a begin() and end() member function, so that you can iterate through it withTo actually solve the problem, maybe in a Heavy-Light style, I kept also for each vertices a pointer to the leaf of its heavy-path, so that I could only change the answer in the leaf.
My full implementation of lomsat gelral can be found here
Hi , Arpa, I used this technique to solve 600E - Lomsat gelral, its a very neat technique.. but wont this get a MLE? I am getting a MLE with the O(nlog^2n0 method ,.. I saw your solution and I see its the same as mine, but mine gets MLE.. My solution :- 39325497
Solutions for Educational Codeforces Round 2 is private, nobody can't see your code. Perhaps you do not use pointers, dynamic memory allocation, and memory cleanup. In this technique it is forbidden to copy huge containers.
I solved this problem with Euler tour on tree and Mo algorithm in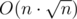 time and O(n) memory. Code.
time and O(n) memory. Code.
Great blog but I am not able to understand the logic behind the O(nlogn) solution it would be a great help if anyone can explain it.
I have a question for style 3 i.e HLD style.
I'm not so sure what's happening in there, I have 2 assumptions. Both of them are wrong, so it would great if someone could point out the mistake and explain what's right.
We are in root.
We first go down the light edges of root and when we finish with them, we clear the cnt array, so there is absolutely nothing left in it and then we proceed to the heavy child of the root and then we just update cnt array.
Now we go back to the light edges of the root and (here's the problem) as the cnt array only contains information for the heavy child of the root, we must go through EVERY vertex in subtrees of light children of the root. If we don't go to the heavy children in the subtrees (as it proposes in tutorial?), then the answer is wrong, as we didn't count them (remember that we cleared the cnt array).
We first go down the light edges of the root, but this time, for every heavy child, we keep the information.
But then as we proceed to the heavy child of the root, the array cnt won't be empty and the answer for heavy child will be incorrect.
Consider you entered vertex v, let it's heavy child h. First, go to all child of v except h and calculate the answer for them and each time clear the cnt array. Then go to h and calculate the answer and don't clear the cnt array. Then traverse all of the subtree of v except subtree of h, and add them to cnt.
I got it, thanks for the quick reply!
Another problem can be solved with this technique. Arpa please add this one in the list.
http://mirror.codeforces.com/contest/1009/problem/F (Dominant Indices)
Can someone explain why this solution 40510312 is getting TLE on problem 600E - Lomsat gelral. I'm using style 4.
Can't view your submission
Firstly, thank you for reaching out to help :). I got my mistake.
I'm continuously getting TLE in test case 30 in 570 : D : Tree Request (The second one given in the blog practice problem) while implementing through DSU similar to what is given here. Submission Id : 40780911 , can somebody make a look over this and provide hint to optimize it.
My solution passed the time limit after replacing endl with "\n".
This blog was a bit code-heavy for me when I first read this. Hence I have tried to simplify the concept a bit more in a more textual fashion in my own tutorial spin-off. I have tried to provide the intuition behind small-to-large merging including small to large on trees, also knows as DSU on trees.
However I. haven't provided any code as the code given by the OP is more than enough.
DSU-on-Tree-Intuition
sorry but you absolutely wrong about the complexity, i know the trick merge smaller to greater but it works when you don't for(i = 0; i < greater.size(); i++) again, but here in O(nlogn ^ 2) you use cnt[v] = cnt[bigchild], it equal to "for(int i = 0; i < cnt[bigchild].size(); i++) {} ", so it's not O(nlogn ^2)
Note that cnt[v] is a pointer.
you mean that it take O(logn) time ?
O(1).
got it, but how about the vector in your O(nlogn) time ?
It's pointer too, isn't it?
thanks a lot, I got it.
Can someone explain, why will the complexity of the first code will be O(nlog^2n)?
Every vertex will appear in cnt's, every time we want to insert a vertex it costs
cnt's, every time we want to insert a vertex it costs  , so the whole time complexity is
, so the whole time complexity is 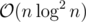 .
.
Thanks :)
This particular problem can be solved in linear time:
Can somebody help me understand why my solution 51874074 for problem 246E - Братья по крови возвращаются gets WA on test 50? I tried to implement the Heavy Light Decomposition style dsu
How to answer online queries using this technique??
I didn't find till today.
why did he declare every time using pointer, can't we simply declare array of map for first approach as map<int,int> cnt[maxx] instead of map<int,int>*cnt[maxx] ?
Due to this line, cnt[v] = cnt[bigChild]. Because we are using pointer, we only pass the reference. In other case, whole map will be copied(time complexity: linear in size of map).
Then, will the information for the child be lost when we modify the parent's map which actually references the child's map... If so then how to answer queries in case when I need to access the nodes' map later?
Yes, it is an offline algorithm. You can use it if you can read all the queries and solve them together.
Why is my code getting TLE for problem 600E — Lomsat gelral? I'm using the technique no. 1 from this tutorial.
your code is working in $$$O(N^2)$$$ .You can't go through the whole $$$(*cnt[u])$$$ to answer queries.
after 2 months!!!
you think he / she, will check this blog again looking for his answer?
Love this.
Thank you for the article.Now I understand it.
Small nitpick: In solution 2, the comment
should be:
Yes, this is correct. I was ready to comment it right now ! Arpa
Fixed.
For everyone who needs an explanation, here is a blog.
And obviously, thank you Arpa for this wonderful content!
Thanks a lot really.
For heavy-light decomposition style for the first add(v,p,1) except the big child sub-tree we are visiting the whole sub-tree of all the light children. Also for second add we are visiting again all the sub-tree if keep==0. How does the complexity becomes $$${O(nlogn)}$$$. Having a hard time to understand, please can anyone tell me how is the complexity calculated.
For each vertex like $$$v$$$, let $$$l(v)$$$ number of light edges in the path from the root to $$$v$$$. Add function called on $$$v$$$, $$$l(v)$$$ times. $$$l(v) \in \mathcal{O}(\log n)$$$, so overall complexity is $$$\mathcal{O}(n \log n)$$$.
For second add function we have made big[bigChild]=0 for all bigChilds in subtree. Now when we call add(v,p,-x) the whole subtree is visited. How does this make complexity $$${O(nlogn)}$$$
We're deleting all the children only when the current node is not a bigChild, so that it doesn't mess up the global data structure. When the current node is a bigChild, then
keep=1, and no data regarding the current subtree is deleted.Can we know the shortest distance from a vertex using dsu ?
I tried solving 208E - Братья по крови using the first approach as explained in this blog but getting MLE on test case 59. I'm not able to figure out why it's giving MLE. Please help!
Here is the link to my submission : 80790329
Thanks!
https://www.hackerearth.com/problem/algorithm/monkeys-on-a-tree-0fe98ed9/
This problem can also be done by dsu on trees.
cnt[v] = new map<int, int> ();
Why are we doing this? My code gave segmentation fault without this.
cnt[v] is not a map. It is "pointing" to a map. This is because we don't want to re-assign all the values of the bigChild to v, but rather just change the "pointer", which is a lot faster. Of course by doing that, we are affecting the subtree of the bigChild as well, but we have already replied to queries related to the bigChild's subtree. That is, because here we have a pointer, we need to assign to cnt[v] a "new map", whenever it is pointing to a NULL, else you will get seg-fault.
Very late, but this problem (Educational Round 91 E) is a very recent problem that can be solved with this technique.
Nice
Hello AmirAz, I tried to submit a similar solution to yours for the problem Water Tree but it was giving tle on case 20. Can you tell me what to did you exactly took care of to reduce time complexity?
Arpa Can you tell me why his solution got accepted but mine failed (tle) on test 20?
Great practice problems! Thanks for the tutorial Arpa.
ِYou're welcome.
Sorry for necroposting.
I felt this could be helpful for people trying to learn this great technique.
https://mirror.codeforces.com/problemset/problem/1363/E
My submission: https://mirror.codeforces.com/contest/1363/submission/125449811
Very useful blog! Thank for Arpa. I also looking forward to seeing an update on the problem list as there are many new forms of problems to be solved by this technique nowadays. As far as I know, some problems can even be associated with data structures, such as this.
Can anyone please help, why we need bigChild here, why don't we have direct DFS and where child returning map of cnt.
That's the main crux of the small-to-large merging.
Let's say you have n children maps with sizes x1, x2 , ... , xn. Then instead of creating a new set for parent and then merging all n sets one by one, We can start with the bigChild and merge all other children's maps into it.
Same thing is happening here, we are not clearing the bigChild's info so it can be use as base and then we are adding all other children's info.