665A - Buses Between Cities
The problem was suggested by Sergey Erlikh unprost.
Consider the time interval when Simion will be on the road strictly between cities (x1, y1) (x1 = 60h + m, y1 = x1 + ta). Let's iterate over the oncoming buses. Let (x2, y2) be the time interval when the oncoming bus will be strictly between two cities. If the intersection of that intervals (x = max(x1, x2), y = min(y1, y2)) is not empty than Simion will count that bus.
Complexity: O(1).
665B - Shopping
The problem was suggested by Ayush Anand JeanValjean01.
In this problem you should simply do what was written in the problem statement. There are no tricks.
Complexity: O(nmk).
665C - Simple Strings
The problem was suggested by Zi Song Yeoh zscoder.
There are two ways to solve this problem: greedy approach and dynamic programming.
The first apprroach: Considerr some segment of consecutive equal characters. Let k be the length of that segment. Easy to see that we should change at least 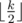 characters in the segment to remove all the pairs of equal consecutive letters. On the other hand we can simply change the second, the fourth etc. symbols to letter that is not equal to the letters before and after the segment.
characters in the segment to remove all the pairs of equal consecutive letters. On the other hand we can simply change the second, the fourth etc. symbols to letter that is not equal to the letters before and after the segment.
The second approach: Let zka be the minimal number of changes so that the prefix of length k has no equal consecutive letters and the symbol s'k equals to a. Let's iterate over the letter on the position k + 1 and if it is not equal to a make transition. The cost of the transition is equal to 0 if we put the same letter as in the original string s on the position k + 1. Otherwise the cost is equal to 1.
Complexity: O(n).
665D - Simple Subset
The problem was suggested by Zi Song Yeoh zscoder.
Consider the subset A that is the answer to the problem. Let a, b, c be the arbitrary three elements from A and let no more than one of them is equal to 1. By the pigeonhole principle two of three elements from a, b, c have the same parity. So we have two integers with even sum and only one of them is equal to 1, so their sum is also greater than 2. So the subset A is not simple. In this way A consists of only two numbers greater than one (with a prime sum) or consists of some number of ones and also maybe other value x, so that x + 1 is a prime.
We can simply process the first case in O(n2) time. The second case can be processed in linear time. Also we should choose the best answer from that two.
To check the value of order 2·106 for primality in O(1) time we can use the simple or the linear Eratosthenes sieve.
Complexity: O(n2 + X), where X is the maximal value in a.
665E - Beautiful Subarrays
The problem was suggested by Zi Song Yeoh zscoder.
The sign  is used for the binary operation for bitwise exclusive or.
is used for the binary operation for bitwise exclusive or.
Let si be the xor of the first i elements on the prefix of a. Then the interval (i, j] is beautiful if 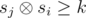 . Let's iterate over j from 1 to n and consider the values sj as the binary strings. On each iteration we should increase the answer by the value zj — the number of numbers si (i < j) so
. Let's iterate over j from 1 to n and consider the values sj as the binary strings. On each iteration we should increase the answer by the value zj — the number of numbers si (i < j) so 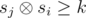 . To do that we can use the trie data structure. Let's store in the trie all the values si for i < j. Besides the structure of the trie we should also store in each vertex the number of leaves in the subtree of that vertex (it can be easily done during adding of each binary string). To calculate the value zj let's go down by the trie from the root. Let's accumulate the value cur equals to the xor of the prefix of the value sj with the already passed in the trie path. Let the current bit in sj be equal to b and i be the depth of the current vertex in the trie. If the number cur + 2i ≥ k then we can increase zj by the number of leaves in vertex
. To do that we can use the trie data structure. Let's store in the trie all the values si for i < j. Besides the structure of the trie we should also store in each vertex the number of leaves in the subtree of that vertex (it can be easily done during adding of each binary string). To calculate the value zj let's go down by the trie from the root. Let's accumulate the value cur equals to the xor of the prefix of the value sj with the already passed in the trie path. Let the current bit in sj be equal to b and i be the depth of the current vertex in the trie. If the number cur + 2i ≥ k then we can increase zj by the number of leaves in vertex 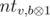 , because all the leaves in the subtree of tha vertex correspond to the values si that for sure gives
, because all the leaves in the subtree of tha vertex correspond to the values si that for sure gives 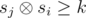 . After that we should go down in the subtree b. Otherwise if cur + 2i < k then we should simply go down to the subtree
. After that we should go down in the subtree b. Otherwise if cur + 2i < k then we should simply go down to the subtree  and recalculate the value cur = cur + 2i.
and recalculate the value cur = cur + 2i.
Comlpexity by the time and the memory: O(nlogX), where X is the maximal xor on the prefixes.
665F - Four Divisors
The editorial for this problem is a little modification of the materials from the lecture of Mikhail Tikhomirov Endagorion of the autumn of 2015 in Moscow Institute of Physics and Technology. Thanks a lot to Endagorion for that materials.
Easy to see that only the numbers of the form p·q and p3 (for different prime p, q) have exactly four positive divisors.
We can easily count the numbers of the form p3 in 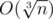 , where n is the number from the problem statement.
, where n is the number from the problem statement.
Now let p < q and π(k) be the number of primes from 1 to k. Let's iterate over all the values p. Easy to see that 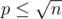 . So for fixed p we should increase the answer by the value
. So for fixed p we should increase the answer by the value 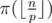 .
.
So the task is ot to find 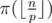 — the number of primes not exceeding
— the number of primes not exceeding  , for all p.
, for all p.
Denote pj the j-th prime number. Denote dpn, j the number of k such that 1 ≤ k ≤ n, and all prime divisors of k are at least pj (note that 1 is counted in all dpn, j, since the set of its prime divisors is empty). dpn, j satisfy a simple recurrence:
dpn, 1 = n (since p1 = 2)
dpn, j = dpn, j + 1 + dp⌊ n / pj⌋, j, hence dpn, j + 1 = dpn, j - dp⌊ n / pj⌋, j
Let pk be the smallest prime greater than  . Then π(n) = dpn, k + k - 1 (by definition, the first summand accounts for all the primes not less than k).
. Then π(n) = dpn, k + k - 1 (by definition, the first summand accounts for all the primes not less than k).
If we evaluate the recurrence dpn, k straightforwardly, all the reachable states will be of the form dp⌊ n / i⌋, j. We can also note that if pj and pk are both greater than  , then dpn, j + j = dpn, k + k. Thus, for each ⌊ n / i⌋ it makes sense to keep only
, then dpn, j + j = dpn, k + k. Thus, for each ⌊ n / i⌋ it makes sense to keep only  values of dp⌊ n / i⌋, j.
values of dp⌊ n / i⌋, j.
Instead of evaluating all DP states straightforwardly, we perform a two-step process:
Choose K.
Run recursive evaluation of dpn, k. If we want to compute a state with n < K, memorize the query ``count the numbers not exceeding n with all prime divisors at least k''.
Answer all the queries off-line: compute the sieve for numbers up to K, then sort all numbers by the smallest prime divisor. Now all queries can be answered using RSQ structure. Store all the answers globally.
Run recurisive evaluation of dpn, k yet again. If we want to compute a state with n < K, then we must have preprocessed a query for this state, so take it from the global set of answers.
The performance of this approach relies heavily on Q — the number of queries we have to preprocess.
Statement. 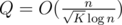 .
.
Proof:
Each state we have to preprocess is obtained by following a dp⌊ n / pj⌋, j transition from some greater state. It follows that Q doesn't exceed the total number of states for n > K.
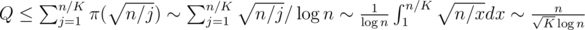
The preprocessing of Q queries can be done in 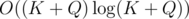 , and it is the heaviest part of the computation. Choosing optimal
, and it is the heaviest part of the computation. Choosing optimal 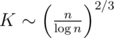 , we obtain the complexity
, we obtain the complexity 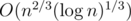 .
.
Complexity: 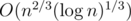 .
.











Auto comment: topic has been updated by Edvard (previous revision, new revision, compare).
This problem is also an easier version of This Problem !
That's why you were able to solve it?
Yeah!
Cool. :)
Endagorion told me that there are something very similar at Project Euler. Also the problem to count semiprimes was last year at MIPT camp (the editorial from there). Anyway I think it's very good problem for Educational Round.
Funny:
A bit harder maybe, but all the same.
Can you explain your solution or provide some link to the theory behind it? It looks much simpler than author's.
Let S(v,m) be the count of integers in the range 2..v that remain after sieving with all primes smaller or equal than m. That is S(v,m) is the count of integers up to v that are either prime or the product of primes larger than m.
S(v, p) is equal to S(v, p-1) if p is not prime or v is smaller than p2. Otherwise (p prime, p2<=v) S(v,p) can be computed from S(v,p-1) by finding the count of integers that are removed while sieving with p. An integer is removed in this step if it is the product of p with another integer that has no divisor smaller than p. This can be expressed as
S(v,p)= S(v,p−1)− ( S(v/p, p−1)− S(p−1,p−1) ).
During computation of S(N,p) it is sufficient to compute S(v,p) for all positive integers v that are representable as floor(N/k) for some integer k and all p ≤ v1/2.
NOTE: Pi(N) = S(N,N). When you call S(N,N) it will need to compute S(N/k,N/k) in its lower substate. Hence you can have all required values of Pi(N/k).
In my code DSUM(N,P) do the job of calculating S(N,P).
I used two arrays H[] and L[] for storing the values of S(N/k,p) in H[k] for k<=N1/2 and for k>=N1/2 I stored the values of S(N/k,p) in L[N/k].
For computation I started with p=2 and changed the values of all the state which is going to be affected by this particular prime. Continue doing this for all prime till N1/2 and at the end for k<=N1/2, H[k] will contain the values of Pi(N/k) and L[k] will contain the values of Pi(k).
PS: My complexity is O(N3/4).
Idea: This Post!
Can I get your code please ???
Can you explain why the time complexity of your solution is O(N3 / 4)
(I find it difficult to calculate it)
Let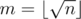 .
.
Notice that v could only be i or , where 1 ≤ i ≤ m, and for each S(v, v) we would enumerate
, where 1 ≤ i ≤ m, and for each S(v, v) we would enumerate 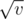 values to calculate it. So the time complexity of the above algorithm is
values to calculate it. So the time complexity of the above algorithm is
The former part is always smaller than the latter, so we could only analysis the complexity of the latter part, which would be same order as
and it's $O(n^{3/4})$ .
By the way, if you preprocess the π(m) for m ≤ n2 / 3, you could find that the integral becomes
and it's $O(n^{2/3})$ . :)
I got AC there with the simple modification of the solution described in editorial:
Is it possible to find these materials?
I think he means to refer to this http://www.ams.org/mcom/1996-65-213/S0025-5718-96-00674-6/S0025-5718-96-00674-6.pdf
In problem F, how the recurrence dp(n, j) = dp(n, j + 1) + dp(⌊ n / pj⌋, j) is being derived?
Here's what i think:
dp(n,j) counts all positive integers k with the properties:
Now we can split this set into 2 disjoint subsets:
k2 = pjar1a1r2a2... rvav = pj * k3,
where pj is the j-th prime number and r1, r2, ..., rv are all primes bigger than or equal to pj.
k3 is a number obviously in the range [1...⌊ n / pj⌋] with every factor in its PPF (Prime Power Factorization) being at least pj.There are dp(⌊ n / pj⌋,j) such numbers,so the recursion is correct.
In problem D, "Let's define a subset of the array a as a tuple that can be obtained from a by removing some (possibly all) elements of it ". Is there exists any case where (possibly all) all elements will be removed,i can`t fix it..
No.
What is the best approach for B if the constraints were higher (10^5 instead of 100 ) ?
I have only one idea to optimise it to O(n*k*log(m)) using segment tree.
using penwick tree , we can solve O(n*m*log(k+n*m))
first we set the value Position[i] = position
a1 , a2 ,a3 ,.... an
Position[a1]= n*m+1, Position[a2]= n*m+2,... Position[ak] = n*m+k
and make variable pos = n*m;
and initialize penwick tree using Position[i] .
if we find item X, then add penwick_query(Position[x]) to return value.
and decrease_penwick(Position[x],-1) , Position[x]= pos--, penwick_increase(Position[x],1);
above action's time complexity is O(log(n*m+k) ).
do you mean fenwick tree?
also you can write an O(n*m*log(k)) solution with ordered set.
http://mirror.codeforces.com/contest/665/submission/19748159
In problem F, can someone explain the two-step process of evaluating the DP States better?
Can someone explain me the condition cur+2^i >=k in problem E?
A question regarding problem E. When I was solving the problem, instead of writing
int b = (x >> i) & 1;, I wroteint b = x & (1 << i). This change gave me AC (iwas in the same bounds as in the c++ solution).What's the difference?
Good day to you :)
It returns different value:
int b = (x >> i) & 1;Returns 1, if ith bit is 1int b = x & (1 << i);Returns 2^i, if ith bit is 1Hard to say, what happened next (for futher investigation, more code would be needed)
Hope it helped a bit ~ Good Luck :)
can anyone plz explain D in detail !
unable to grab it!
thnxxxx
1.If there's multiple ones in original set, we should choose them, because 1+1=2, 2 is a prime number.
2.Now consider what are the extra elements we should insert into the answer. I donate the answer is {1,1,....,1,A,B,C,....}, look at the {1,A,B}, there are three elements, each of them must be odd or even, so there must be two element have the same parity, so add them together will get a even number larger than 2, that is definitely not a prime number.
3.So you see, if we exclude all the ones in the answer, the answer size must less or equal to 2.
ans(Problem E) == (n * (n + 1) / 2) — ans(http://www.spoj.com/problems/SUBXOR/)
Hey guys, I use the DFS to solve problem D. I'm confused why my code passed test 11 only used 78ms where n equals to 1000, but get a TLE at test 12? here's my solution:code
Thanks
For E: Can someone please explain why we have to flip the bit b in function get()?
Thank you.
Can someone explain what is RSQ structure? It is mensioned in problem F. Had no idea what it is. Thanks.
Could somebody explain me in problem E, why do we have to go down to the subtree (b xor 1) when (cur + 2^i) < k ?
In problem E , L can equal to R . So I think we should check each elements of the array if it >= k
mạnh
Now we can simply solve the problem F with min_25 sieve in $$$O(\frac{n^{\frac{3}{4}}}{\log n} + \sqrt n)$$$ !!
I sincerely agree with you. :)
And notice that you need to calculate $$$\pi(\lfloor\frac n x\rfloor)$$$, choose Meissel-Lehmer and combine with min-25 can you reach a more efficient solution.