You're given a rooted tree with N nodes and Q queries in each query you have an integer K and you want to delete the nodes of the tree the only restriction of deleting some node is that it must be either the root or its parent must be deleted and you can delete at most K nodes each second, what is the minimum time for deleting all nodes?
N <= 10^6 Q <= 10^6










Reverse time — you can cut only leaves.
Some technical arguments shows that you should cut k leaves with largest depths. After some math you can get result that answer is equal to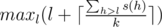 , where s(h) is number of leaves on depth h. That is a trivial lower bound, to prove it is also upper bound is what is nontrivial. From that you can get some disguised geometrical interpretation with hull.
, where s(h) is number of leaves on depth h. That is a trivial lower bound, to prove it is also upper bound is what is nontrivial. From that you can get some disguised geometrical interpretation with hull.
(Not sure why, but CF seems to have hard time showing that formula in latex, here it is: max_{l} (l + \lceil \frac{\sum_{h > l} s(h)}{k} \rceil)
How do you prove that cutting leaves with largest depths is optimal?
In fact that is not the exactly the statement we want to prove ;p. What is important is that bound, so focus on proving that one. Right now I don't feel like delving into details of that problem, I gave you right direction ;p.
Can you pleas upload the formula img on a different site
Can't you do it by yourself? You already have the correctly formatted formula. Or parse it with your eyes, it's really easy.