→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | Dominater069 | 154 |
| 8 | awoo | 154 |
| 10 | luogu_official | 150 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/23/2024 14:20:47 (k2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










I haven't seen that randomized algo to intersecting halfplanes earlier, but I think it's worth noting that main idea is almost the same as in Smallest Enclosing Circle problem (does there even exist deterministic algo with similar complexity?)
Yes, it's quite similar. I'm surprised you didn't see this one before — I had the feeling of being the last one to the party when I learned about it :)
Maybe that's because I am quite satisfied with online half-planes intersection working in that pompon left in our library :).
that pompon left in our library :).
Can you please share your library here ?
I think that I know a different solution to the half-plane problem. Instead of doing binary search, let the value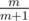 gradually decrease and look at the polygon where O must be located. Initially, when
gradually decrease and look at the polygon where O must be located. Initially, when 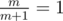 , this polygon is the same as the input polygon. When the value is decreased, the sides move inwards at constant speed which can be determined in linear time using rotating calipers algorithm. The lengths of the sides decrease linearly, so it is possible to find the times when each length would reach zero. When the length of a side becomes zero, adjacent sides will begin shrinking faster, so it is necessary to emulate this process and to recompute the times for adjacent sides when one of the sides disappears. This can be easily done in
, this polygon is the same as the input polygon. When the value is decreased, the sides move inwards at constant speed which can be determined in linear time using rotating calipers algorithm. The lengths of the sides decrease linearly, so it is possible to find the times when each length would reach zero. When the length of a side becomes zero, adjacent sides will begin shrinking faster, so it is necessary to emulate this process and to recompute the times for adjacent sides when one of the sides disappears. This can be easily done in  time using a heap. So, this solution works in
time using a heap. So, this solution works in  time, doesn't use binary search and is completely deterministic.
time, doesn't use binary search and is completely deterministic.