number of pairs (i,j) s.t. 1<=i<=n, 1<=j<=m s.t. i^j = k in O(max(log n, log m)). I am able to do it in min(n,m).
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/23/2024 02:40:16 (j3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











I will be very puzzled if that problem has a solution with logarithmic running time. And I hope that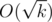 is sufficient. But if the prime factorization of k is known maybe I can solve it in
is sufficient. But if the prime factorization of k is known maybe I can solve it in 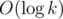 .
.
Consider the prime factorization of k: k = p1k1p2k2... prkr , and we want to find a number of representations looks like ab = (p1a1p2a2... prar)b = p1k1p2k2... prkr .
Let g = gcd(k1, k2, ... , kr) . All of valid representations looks like (p1k1 / dp2k2 / d... prkr / d)d , where d is any divisor of g.
To satisfy 1 ≤ a ≤ n constraint we find min d such that (p1k1 / dp2k2 / d... prkr / d) ≤ n through binary search. It`s minimal valid d. Constraint 1 ≤ b ≤ m gives us maximal valid value of d. And answer is dmax - dmin + 1 .
Hm, maybe ^ is xor?
Fuck... ;)
But it is very easy to solve task in such representation with logarithmic running time. We just need to go through j and check
Can you please share the problem link?
We need to find number of pairs (A, B) such that their XOR is K.
Consider binary representations of K — if some bit is 1 then respective bits in A and B must be different, and if bit is 0 then they need to be same.
Now we can represent N and M in binary and then solve it with DP[prefix][flag1][flag2].
prefix — how many bits are already placed in A and B.
flag1 — 0 if current prefix of A is same as prefix of N and 1 if it is less. flag2 is same as flag1 but for B.