Can anyone provide an explanation for this problem!! I am not able to understand the basic idea.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/23/2024 02:37:54 (l2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










the sum =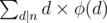
where d is a divisor of n and φ(x) is euler's totient function ... I don't have a proof for it ,I thought it was symmetric to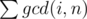 which is equal to (from oeis)
which is equal to (from oeis) 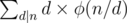 and it worked
and it worked
you can precompute φ in O(n log n) after sieve
and you can generate all divisors of a number in O(number of divisors) using the information generated by sieve
then you can evaluate this sum in O(number of divisors) ... I don't know if that is enough to pass the TL .. because when I solved this problem I reduced the above sum into a function of the the prime factorization and hence I could evaluate it in O(log x) for any x
The main claim is that the sum is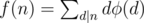 .
.
This can be proved easily since there are exactly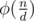 numbers with
numbers with 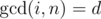 and i ≤ n.
and i ≤ n.
Now, since dφ (d) is a multiplicative function, so is f(n).
Therefore, we can calculate f for prime powers and multiply the results to get f(n).
It turns out — that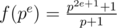 .
.
Now, preprocessing the Eratosthenes's Sieve in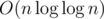 , we can now perform prime factorization in
, we can now perform prime factorization in  . It is easy to calculate f once we have the prime factorization.
. It is easy to calculate f once we have the prime factorization.
Therefore, the time complexity is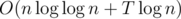 which is good enough to pass.
which is good enough to pass.
I solved it using Pillai's Arithmetic Formula.
Since gcd(i, N)1 < = i < = N is one of the divisors of N hence in order to compute the summation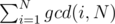 we need to find the sum
we need to find the sum 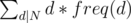 . Now we need to find freq(d) .We need to find the number of i's such that gcd(i, N) = d hence i = d * j when you substitute this in the previous equation you'll get this gcd(j, N / d) = 1 . This equation means that we need to find the number of numbers less than N / d that are coprime with N / d . This is called Euler's totient function.That is how you get this equation
. Now we need to find freq(d) .We need to find the number of i's such that gcd(i, N) = d hence i = d * j when you substitute this in the previous equation you'll get this gcd(j, N / d) = 1 . This equation means that we need to find the number of numbers less than N / d that are coprime with N / d . This is called Euler's totient function.That is how you get this equation 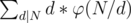
Now coming to the codechef problem , the only change that you need to make is to substitute d with N / d . Hence the sum now becomes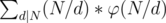 which same as writing
which same as writing 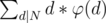
Try solving now.
i implemented what Noureldin and bhishma are talking about but i am getting TLE. here is my code what i did found totient[i] — n loglogn compute ans[i] — that too is n loglogn