P_Nyagolov's blog

An Interesting Problem with Tree
By P_Nyagolov, history, 8 years ago, In English

Hello everybody,

Recently I decided to look for some problems involving queries on trees and the last I found was this — http://acm.timus.ru/problem.aspx?space=1&num=1752 (note that this is not the problem I am asking about). In short, there is an unweighted tree with N<=20000 nodes and Q<=50000 queries are given. Each query contains a vertex V and distance D. You are to find some vertex that is on distance exactly D from V or report that there is no such vertex.

The problem above has a fairly simple solution if you have solved some problems about diameters and LCA. However, when I first read the problem, I misunderstood it and I thought it was asking for how many vertices are there such that the distance from them to V is exactly D. After spending an hour of thinking, I looked at the discussions for some hints and I saw that this was not the problem.

Anyway, I think the problem which I thought I should solve is quite interesting and I wonder if someone has a solution to it. If so, please share your ideas. Also, I would love it if you can give me some more problems about queries on trees, here is one I really liked — http://www.spoj.com/problems/DRTREE/ and also one prepared by myself — http://www.spoj.com/problems/MAXCHILDSUM/.

Thanks in advance! :)

  • Vote: I like it
  • +44
  • Vote: I do not like it

»
8 years ago, # |
← Rev. 2   Vote: I like it +2 Vote: I do not like it

I think that something similiar exists on CF: http://mirror.codeforces.com/problemset/problem/337/D

Thanks on those problems :)

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Well, I have already solved this one but it's way simpler because here we have only one D and we have that threshold for each of the given M vertices so we can easily loop over all nodes and check them. In the problem I asked about we can't check all nodes for every query and this makes it harder, I believe.

    → Reply
»
8 years ago, # |
  Vote: I like it +29 Vote: I do not like it

I don't have time to elaborate, but centroid decomposition should take care of this without much difficulty.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it -21 Vote: I do not like it

    The solution is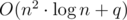 right? Or is there something better?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 3   Vote: I like it +12 Vote: I do not like it

      The complexity is actually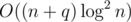 . You can solve it in a similar way to this problem from 1st Hunger Games by PrinceOfPersia. The difference is that in author's problem the distance must be exactly D while in the one I linked the distance should be  ≤ D.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        Can you explain your solution in more details? My solution is to basically to do centroid decomposition and then find number of nodes at distance x from each of those and store in D. Later iterate and remove all nodes in one part from this D count. Now for each node in that part, find answer for nodes at distance x as D[x - dist(centroid, node)]. Later, just answer from this pre computed array. First part works in as for each node as height of centroid tree is . Is there anything wrong with this?

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it +19 Vote: I do not like it

          The idea is almost the same (if I have correctly understood your solution). In your solution you precompute the answer for every vertex and every distance. You can simply solve all queries offline. The idea is that we don't need to save the number of nodes on distance x for every possible distance, so we can add queries one by one to the centroid tree. Each query will appear times but with different x. When we are at a node we answer all queries simultaneously — we find the distance to each node in the current subtree and then just answer the queries with binary search (if the problem is for distance equal to exactly x we can actually simply have an array for the count). The number of queries we will need to answer is 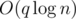and each one of them has complexity of so the overall complexity is 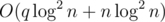. If we used an array for the count (for the problem proposed by the author) the complexity would be just .

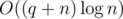          We can actually solve the problem online. We do the same centroid decomposition, but we will do the binary search immediately after the query comes. We need to do binary searches so the overall complexity again will be .

          → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

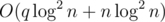    Okay, I will think more in this direction, thank you! :)

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +11 Vote: I do not like it

Btw does anyone know how to solve DRTREE online or if it is even possible? The only solution that came to my mind was the offline approach of solving queries for every root in O(N + Q).

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +22 Vote: I do not like it

    I once wrote the solution in other posts :

    http://mirror.codeforces.com/blog/entry/43617#comment-282866

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think we can also solve this using treap on DFS order online. When changing root, simply remove the subtree from DFS order and place it back just after entering node. This is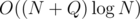 with slightly high constant...

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I had the same idea but won't this work only if the new root and previous root are adjacent? Thanks in advance :)

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 3   Vote: I like it +13 Vote: I do not like it

        You're probably just enumerating over a node once in your euler tour. If you modify it to add the node whenever you visit even some other node through it, it should work for re rooting to all nodes. Basically by doing so, you do an Euler tour of the edges, i.e. you try to linearize the tree in form of edges. I tried it on a couple of complicated examples and it seemed to work ok. Please reply if it doesn't work on some case. After making the euler tour as above, to get the new DFS order first remove the sub array corresponding to the subtree of the node you remove. Now put the newly obtained array(without this subtree), right after the first occurrence of the node itself. You might need a little bit of work to fix duplicates etc(trivial), but it should hopefully work ok. See one of the complicated examples I tried on pen and paper with the part of treap being brought down highlighted(pardon my handwriting). Btw, I think there is also mention of ability to do so in some blog I can't find right now related to treaps(so it should probably work). :)

        P.S. I am too lazy to code and test it right now, will do so soon :P

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          That's a really nice idea! It seems to work. Thanks a lot :)

          → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +4 Vote: I do not like it

COCI 2011-2012 Round 2 problem (place)

You're given a tree with N nodes (N<=5*10^5) and Q queries (Q<=5*10^5).

Every query is one of these two operations :

1- p A V : add value V to all the nodes in the sub-tree of node A .

2- u V : what is the current value in the node V ?

I found it very interesting :D

Sorry for my poor English.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Flatten the tree into an array (using simple dfs). Now, adding a value to all nodes in a subtree can thus be transformed into adding a value to a subarray and querying the value of a node is equivalent to querying a single value. This problem can be solved easily, using Fenwick Tree or Segment Tree for instance.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    A harder version of the problem (same constraints):

    We have the same two operations but also we have:

    3- A u v w : add w to all vertices on path from u to v

    4- Q u v: get sum of all vertices on path from u to v

    5- S u : get sum of all values in u's subtree

    We want to have a solution of order . The solution is pretty easy if you know HLD but still some people might not know how to support both subtree and path queries.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you give a link to such problem?
      Is it solvable without HLD, with Euler Tour maybe?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Well I know a solution only using hld. A problem using this is Round 362 Div. 1 E.

        → Reply
»
8 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Can you please explain how to solve your problem http://www.spoj.com/problems/MAXCHILDSUM/ ?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    But I wouldn't upload it if I tell the solution immediately :D

    However, here are two questions to think about: How could we answer the queries if the nodes didn't have many children? Are there many nodes who have many children?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Do we have to use the fact that atmost sqrt(n) nodes can have more than sqrt(n) children...This approach was leading to a complexity of Qsqrt(n)log(n)...and I feared it wont pass..

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Yeah, I am sorry for that, I will increase the TL to 2.0s whenever I am able to run rejudge, SPOJ doesn't allow me to do it now for some reason. I also wanted to prevent solutions with big constants getting accepted (If you get the idea, you will know that this complexity can be achieved with different DSs and some are slower than other) but I guess it wasn't a good idea :)

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it

          Yes the time limit was very strict...but thanks for the interesting problem..

          → Reply
          • »
            »
            »
            »
            »
            »
            8 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            No problem and sorry for the misleading TL again. I made it 2 seconds now and I will rejudge only the submissions made by this moment but looking at them even a TL of 10s wouldn't help :D

            → Reply
»
8 years ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

Hi! Thanks for this interesting blog! Lot to learn.

I tried to solve the first problem given from Timus (Tree2). I used following approach:

Found the nodes of the diameter of the tree. Made one end node of the diameter the root of the tree. Then when there is a query, I simply went up using sparse table of the parent nodes (like what we do in finding LCA) and reached a node on the diameter. I changed the required distance accordingly.

When I am on the diameter, I simply binary searched on the diameter from the node where I reached. Now this binary search is done both on left side and right side.

I checked several test cases and did not find my mistake. WA on test #5. :(

Is my idea okay? Or am I missing something? Can anyone give me a test case?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Made one end node of the diameter the root of the tree.

    Shouldn't you do that with both ends seperately, because if for vertex V you choose the closest end, then you may answer with 0 while there is an answer between V and the other end?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      But I did the binary search on both sides. I mean after reaching a particular node on the diameter, I binary searched with the remaining distance on left, and then on right. Should not it work?

      Here is my submission: Tree 2

      Check out the function Lovegood where I did the binary search on both sides.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 2   Vote: I like it +8 Vote: I do not like it

        The biggest flaw with your code is that you have functions named Weasely and Dumbledoor.

        The second biggest flaw is that the first thing that Lovegood() does is take pos[u]. But what happens if u is not in the diameter?

        To avoid more flaws when trying to fix this, a word of caution that for binary search to work the function has to be monotonic. So pos[u] can't be any node on the diameter, it has to be a specific one.

        → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Do you know of any problems on timus similar to "Tree 2"?

→ Reply