Let's discuss the solutions of all the problems. I am only able to solve A-Small and A-Large. I would like to know other peoples approaches for the other 3 problems. Also how should I prepare for it to get the rank below 300 in the next round.
Here are the problem statements.











Hints for large:
Problem B: We only need to compute ia and ib for i ≤ k.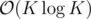
Problem C: Greedy. Remove the segment such that maximum number of points are uncovered. Implement using line sweep to check for moments when exactly one segment is "active".
Problem D: DP. If the size of thr right most chunk is x then it must consist of the largest x elements of the permutation if we want maximum no of chunks. Also such a chunk cannot havr a suffix of size y < x consisting of the largest y elements else the right most chunk can be split into two. Use dp compute number of such right most chunks of size x and use another recurrence to compute the answer for n using information from permutations of size n - x.
Little more detail for problem B ?
ia mod k = (i + k)a mod k
I got that . My solution was O(K^2Log(K)) . I iterated over i and j in [1,K] and if (i^a+j^b)mod K was zero , added ((N-i)/K+1)*((N-j)/K+1) to the answer . How to reduce this to O(KLogK) ?
If you know that ia mod k = r then jb mod k must be k - r. Instead of iterating over i, iterate over the possible remainders of ia and you will know what kind of remainder of jb you are looking for.
I am so stupid -.- .
and how do you check for i!=j ??
hint: check if ia + ib mod k = 0 for all i ≤ k
Didnt get the math behing it ! Explain bit more plz and also do share code
Hi. Would you please discuss about the solution of Problem A as well? Seems like a very easy one but can't seem to get it fully.
Max. no of balanced substrings will be obtained only when he arranges them separately as : ()()()() with extras at one end. No. of single pair balanced = Min( no. of '(' , no. of ')')
So. no. of substrings will be 1 + 2 + .... + (no of balanced pair)
Can u explain B in more detail please . ?? Logic behind only going till i<=k
http://mirror.codeforces.com/blog/entry/46812?#comment-312529
D has a nice soultion that uses only generating functions:
Let
Then the required answer is the coefficient of xn in:
G(x) = P(x)(P(x) - 1)(2P(x) - 1)
I used inclusion-exclusion and infinite GP sum to prove this, but I was thinking a simpler analysis exists considering the simplicity of the formula. Did anyone do it this way?
I don't know generating functions very well, but here's how I would solve this problem:
For each permutation, consider that you can insert a divider after position i if all numbers before i are smaller than i, and all numbers after position i are greater than i. All legal divisions into chunks are splitting numbers into groups according to a subset of these dividers: as we're only interested in the maximum division, we'll always pick them all.
Now note that within a permutation, as the number of dividers is f(n), it follows that the number of pairs (a, b) such that 1 ≤ a, b ≤ n and a, b are both possible dividers is exactly equal to f(n)2. Therefore, we can simply count, for each pair (a, b), in how many permutations it is a valid pair.
And this is easy to count: pair (a, b), a ≤ b, is valid in a! × (b - a)! × (n - b)! permutations. We should multiply this by 2 if a < b, because we the symmetric pair (b, a) is also valid.
It shouldn't be too hard to see why this calculation is actually equivalent to your generating function.
How did you deduced out this function? could you please list the deduce process?
Can you explain C small as well as large in more detail ?
A classic technique for segments covering problem: regard a segment [x, y] as 2 marks: {x, a segment begins} and {y, a segment ends}. Sort all these marks, deal them from left to right.
For the original problem, the total coverage area - the maximum area which is covered only by one specific segment, is the answer we are looking for.
we can deal with both two parts using the same technique: maintain a set, representing the segments which are covering till this mark. The area is covered if the set has at least one element. The area is covered by only one segment if the set has only one element, which is also the owner of the area which is just covered by only one segment.
For those Chinese readers: I've written my own solutions at http://blog.csdn.net/fcxxzux/article/details/52346364 , and I'll continue updating this blog for the following 3 rounds.
For those non-Chinese users, you may use Google Translate.
Translating Chinese into English manually is tiring, and that solution is for, well, dummys .I'll write some key points here.
B: since ia mod k = (i + k)a mod k, all the possible values of i (in 1~n) can be classified into at most k categories by mod k = 0... (k - 1)
C: A classic technique for segments covering problem: regard a segment [x, y] as 2 marks: {x, a segment begins} and {y, a segment ends}. Sort all these marks, deal them from left to right.
For the original problem, the total coverage area — the maximum area which is covered only by one specific segment, is the answer we are looking for.
We can deal with both two parts using the same technique: maintain a set, representing the segments which are covering till this mark. The area is covered if the set has at least one element. The area is covered by only one segment if the set has only one element, which is also the owner of the area which is just covered by only one segment.
D: First, you need to figure out the number of primitive chunk with length 1... n, which can't be divided into smaller chunk. Here's the formula: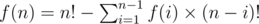
After this calculated, it's fairly easy to figure out the O(n3) dp: dp[i][j] indicates how many permutations with length = i and can be divided into at most j chunks. Adding a primitive chunk behind a state will work here. And the answer will be dp[n][1] × 12 + dp[n][2] × 22 + ... + dp[n][n] × n2
As for the O(n2) solution, It's a little bit tricky: instead of calculating the numbers of permutation and figuring out the answer we need later, we will try to directly calculating the answer, i.e.,for i = 1... n, calculate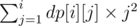 . With some calculation on paper, you'll find that calculating dp[i][j], dp[i][j] × 2j and dp[i][j] × j2 will solve this problem.
. With some calculation on paper, you'll find that calculating dp[i][j], dp[i][j] × 2j and dp[i][j] × j2 will solve this problem.
Hey. I couldn't understand the solution to C problem. Please can you elaborate more?
Let's start with a more simple problem.
You are given some logs for the using statistic of one resource. each row indicates a user used this resource from start time to end time. A row of log is like :Tuple<TIMESTAMP,TIMESTAMP> , the first one (.Item1) is start time, and the second one (.Item2) is the end time.
Now you should figure out the total time the resource is used by someone. If two or more persons are using this resource at the same time, regard that as one.
For Example, here's some record:
the answer is 4,since there are users using this resource at {1,2},{2,3},{3,4} and {5,6}(two users are using this resource at {2,3}, regard that as one.)
A typical solution is: using an array like bool[] usedBySomeone ,then:
Which is slow.
Let's use the technique we mentioned above:
make a new array for those record, then sort them by TIMESTAMP, you'll get:
and Let's deal them from the beginning to the end:
{1,start}: now there's one user using this resource, count = 1, also we need to record the start time : startStamp = 1
{2,start}: now there're two user using this resource, count = 2
{3,end}: now there's two user using this resource, count = 1
{4,end}: now there's no user using this resource, count = 0. Then we need to add the time we just checked with at least one user using to the answer. Answer += this.TIMESTAMP — startStamp = 4 — 1 = 3
{5,start}: now there's one user using this resource, count = 1, also we need to record the start time : startStamp = 5
{6,end}: now there's no user using this resource, count = 0. Then we need to add the time to the answer. Answer += this.TIMESTAMP — startStamp = 6 — 5 = 1
so we have the answer: 3 + 1 = 4
Hope this can help you understand my solution better. If you need further explanation, please tell me.
Hi! Would you please explain how you came up with the formula for f(n) in Problem D?
f(2)=1 and f(3)=3, what do these values actually represent?
f(n) is the number of primitive chunks with length 1... n, which can't be divided into smaller chunks.
Let's check what are the permutations counted by the f(n)
f(1) = 1
[1]
f(2) = 1
[2,1]
[1,2] is not the thing we expected ,since we can divide it into [1][2].
f(3) = 3
For those are not:
[1,2,3], we can divide it into [1][2][3]
[1,3,2], we can divide it into [1][3,2]
[2,1,3], we can divide it into [2,1][3]
checking all those non-primitive chunks, you'll find that, all of them starts with a shorter primitive chunk.
So,
=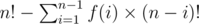
Thanks a lot, this was really helpful. After fumbling around a bit, I managed to implement the O(n^3) solution but still stuck on the O(n^2) solution. I understand the calculation of expanding (b+1)^2 to (b^2 + 2b + 1) but fail to see how this changes the way we solve the problem. To find dp[x][j+1], I'd still need to calculate summation of dp[i][j] * f(x-i) for all i<x, right? Would you please explain this part as well?
Another thing I'm curious about and would be grateful if you answer: how does someone understand that they should think about "primitive chunks" in such a problem? I mean, are most people (who could solve it) already familiar with a similar problem or something? Otherwise, it amazes me how people can come up with such good solutions in a short time, that too in a stressful environment like a contest... And I'm not even talking about the O(n^2) solution.
For the first question, The transform is tricky.
we need to directly maintain, for i = 1... n, calculate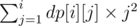 , which will be the result.
, which will be the result.
Let's do some calculation.
dp[a][b]*b^2 is the thing we want to maintain directly here.
dp[a][b], you know how to do it.
As for dp[a][b]*2b
Now you just need to maintain the sum of each part when they are representing the same length.
==========================================
for the second question, in fact, someone else taught me the solution of Problem D (for the O(n^3) part). I think it's just the intuition of experienced competitive programmers? Defining the primitive chunks is a really smart move.