Hello All,
I have some questions as doubts:
1) How can we solve problem E (The secret code) in http://mirror.codeforces.com/gym/100371 Any hints?
2) I am given an sorted array of 1000 elements, where each element can be in the range [0, 20000]. We need to consider all subsequences on the array. For every subsequence, it's power is defined as the sum of all the elements in it. We are given 1000 queries of the form "x" where i need to print the xth smallest value of the power of any subsequence of the array. Here "x" is in the range of [1, min(2^n, 10000)].
For example: Let the array be [1, 2, 100]. Then the power of subsequences sorted order are [0, 1, 2, 3, 100, 101, 102, 103]. If the query is x = 3, I need to print 2.
3) How can we solve this problem https://icpcarchive.ecs.baylor.edu/index.php?option=onlinejudge&page=show_problem&problem=2334
My approach to this problem- First of all if the graph contains a directed cycle, then the answer is 0, as a trivial case. Otherwise, consider all the cases where we can partition the groups into 2 equal halves. For this I use of mask (till 2^(2m)) and if it contains number of set bits as "m" I continue the loop. Then I consider the partition if it is valid or not i.e. if in partition 1 or 2, whether there exits a person "i" who has a dependency on person "j" but is not present in the same set. In such a case, I just add nothing. In rest of the cases, I try to find the number of topological sorts on graph in set 1 and 2 and multiply their results and finally add it to the final result. (For number of topological sorts, I used this method http://cs.stackexchange.com/questions/12713/find-the-number-of-topological-sorts-in-a-tree )
Here is a link to my code according to the above implementation https://textb.org/r/doubt-likecs/
4) How can we efficiently find the points of intersection of a line and polygon, where the polygon is not necessarily convex polygon (but the polygon is simple)?
Please help in the above problems. If possible please post the code as well.
Thanks in advance.











2) There's a good D&C solution for finding the smallest K sums: solve it for two halves of the array and you just need to find the K smallest sums of pairs. Then, you can binsearch the largest sum or use a priority queue to find them in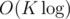 ; that makes the total complexity
; that makes the total complexity 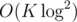 . (I'm assuming different subsequences with equal powers aren't counted as one value, since there can be less than 2^n possible values otherwise and it would take
. (I'm assuming different subsequences with equal powers aren't counted as one value, since there can be less than 2^n possible values otherwise and it would take 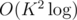 .)
.)
Thanks for the answer.
In above solution, I have assumed that 2 or more subsequences having the same sum are counted more than once.
Your solution is OK but it is a bit slow. For computing the DP, complexity is Max_n * Max_sum = 1000 * 400000 = 4 * 10^8, which is around 4 seconds. I thinks the solution proposed by Xellos is quite good for practical purposes as it doesn't impose any limits on value of A[i] as well.
I know. Just wanted to give an alternative approach. :P
A faster solution for (2).
Let K be the maximum value of the queries (in this case K ≤ 10000). Consider a DAG. For each 0 ≤ i < N, we have two multi-edges i -> i+1 of costs 0 and (i+1)^th element of the array. The paths from 0 to N correspond to subsequences and vice versa. Now, we need to calculate all K-best shortest paths of this graph.
This problem can be solved by Eppstein's algorithm (paper). Because the graph is DAG, Eppstein's algorithm can run in O(N + K) time. For practical purpose, we can omit Frederickson's algorithm and get simpler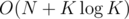 algorithm.
algorithm.
Does a similar solution exists for the problem "1" where i want the k largest products but each number is selected from different array?
BTW, thanks for the links.
Yes. We can solve the problem in a similar fashion.
The DAG now have M multi-edges for each 0 ≤ i < N. It corresponds to the M ways of selecting positions.
Products can be converted to sums by taking logarithm. I think Eppstein's algorithm can be implemented robustly in a sense that floating-point number will work well. Total runtime is O(NM + K) (theoretically).