2016-2017 CT S03E03: Codeforces Trainings Season 3 Episode 3

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Добро пожаловать на 2016-2017 CT S03E03: Codeforces Trainings Season 3 Episode 3 - 2007-2008 ACM-ICPC, Central European Regional Contest 2007 (CERC 07). Продолжительность тренировки — 4 часа 30 минут. Тренировка открыта как для команд, так и для индивидуальных участников. После ее окончания вы можете дорешивать задачи тренировки или поучаствовать в ней виртуально, если не смогли принять участие одновременно со всеми. Пожалуйста, участвуйте в тренировке честно.

Ориентировочный старт: 21 сентября 2016 г., 16:10 (Московское время).

Так как это тренировка, то возможно набор задач будет расширен, если для значительного количества участников он окажется простым.

Условия задач будут на английском языке, ведь мы же готовимся к ACM-ICPC!

Удачи!

#include <fstream> #include <iostream> #include <string> #include <complex> #include <math.h> #include <set> #include <vector> #include <map> #include <queue> #include <stdio.h> #include <stack> #include <algorithm> #include <ctime> #include <memory.h> #include <bitset> #include <climits> #include <iomanip> #define F first #define S second #define endl "\n" #define pb push_back #define mp make_pair #define bs 1000000007 #define pi 3.141592653589793 #define y1 kjdfshnvoavaofobiopj using namespace std; int n, m, ans, final_ans, newary[17][17]; vector<int>myvec; char ary[17][17]; bool error; int dx[] = {-1, 1, 0, 0}; int dy[] = {0, 0, 1, -1}; bool pass(int a, int b) { if(a >= 0 && a < n && b >= 0 && b < m) return true; return false; } int main(){ //freopen("input.txt", "r", stdin); //ios_base::sync_with_stdio(0); //cin.tie(0); while(1) { scanf("%d %d", &n, &m); if(n == 0) break; for(int i = 0; i < n; i++) scanf("%s", ary[i]); final_ans = INT_MAX; for(int mask = 0; mask < (1<<m); mask++) { ans = 0; myvec.clear(); for(int j = 0; j < m; j++) if(mask&(1<<j)) myvec.pb(1); else myvec.pb(0); for(int i = 0; i < n; i++) for(int j = 0; j < m; j++) if(ary[i][j] == 'X') newary[i][j] = 1; else newary[i][j] = 0; for(int j = 0; j < myvec.size(); j++) if(myvec[j]) { ++ans; newary[0][j] ^= 1; int x = 0, y = j; for(int k = 1; k < 4; k++) if(pass(x+dx[k], y+dy[k])) newary[x+dx[k]][y+dy[k]] ^= 1; } for(int i = 1; i < n; i++) { for(int j = 0; j < m; j++) if(newary[i-1][j]) { ++ans; newary[i][j] ^= 1; for(int k = 0; k < 4; k++) if(pass(i+dx[k], j+dy[k])) newary[i+dx[k]][j+dy[k]] ^= 1; } } error = false; for(int i = 0; i < n && !error; i++) for(int j = 0; j < m; j++) if(newary[i][j]) { error = true; break; } if(!error) final_ans = min(ans, final_ans); } if(final_ans == INT_MAX) printf("Damaged billboard.\n"); else printf("You have to tap %d tiles.\n", final_ans); } return 0;}

Комментарии (28)

Показать архивные | Написать комментарий?

bash

8 лет назад, # |

Желаю всем удачи!!!

→ Ответить

-JustSomeDude-

Надеюсь будет весело. Всем удачи.

chintu

← Rev. 3 →

Typo in title: S03E02 (should be S03E03)

8 лет назад, # ^ |

← Rev. 2 →

same typo is in gym page contest name too...

Hamada14

available*

archit522

how to register for it?

Black

+11

Follow this

trunghai95

+44

What's wrong with the problems?

Khina

Please, help me to find a max sum of test cases in problem — A?

Axelius

How to solve Problem Weird Numbers ?

tenshi_kanade

I'll explain my solution, which I'm pretty sure is not optimal.

It's clear that with a negative base, odd positions will be negative and even positions will be positive. So all numbers in base - b can be expressed as e + o where e is some number in base b with all zeroes in odd positions and o is some number in base b with all zeroes in even positions.
So what I did was generate all said numbers up to 10⁹ and store them in E[b] and O[b], where b is the base. Then for every query [b, x] (that is express number x in base - b), I iterate over all e in E[b] and check if e - x is in O[b]. If it is, I just have to print e + o in base b.
The other type of queries is trivial, is just processing a number in base - b.

Thanks for the explanation!!! :)

Morphy

+12

I'll explain my solution, which I think is optimal.

Its almost the same as converting in positive bases. Lets convert N from base 10 to base b (b < 0):

N = a₀·b⁰ + a₁·b¹ + ... + a_n·bⁿ

note that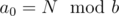 $\text{[math]}$ , so (N - a₀) / b = a₁·b⁰ + ... + a_n·b^n - 1 and we can repeat recursively.

slovak

Anybody knows where can I find the editorial ( :

Thanks

halin.george

Why did answer "4 2 3 4" fail on the second sample? (Problem S. Robotic Sort)

mahmud2690

It is said in statement: their mutual order must be preserved: the one that was given first in the initial order must be placed before the others in the final order too. So you should also consider the INITIAL indexes of elements.

What is solution for problem C(Phone Cell)? We thought that problen can be solved by geometric invertion, but we don't know, how we can use it.

+14

You can find all solutions here: Link

Tehnar

How to solve B? :(

sgtlaugh

Consider all the tiles of row 1. There are m tiles and 2^m ways to select a subset of them to be flipped. Notice that this uniquely determines all the other tiles which needs to be flipped to clear the billboard afterwards.

Consider cell(2,1). If cell(1,1) is on, then cell(2,1) must be flipped. And if (1,1) is off, (2,1) should not be flipped. Because after flipping (2,1), (1,1) is on and now there is no way to turn off (1,1) since the columns to be flipped in row 1 is fixed.

Complexity: O(2^m * n * m)

__STR

I used bitmask but it keeps giving me TLE on test 2, I submitted the same code on SPOJ(where time limit is 3.6sec) it got AC, How to get AC when time limit is 1sec using bitmask?

my code

Shavkat_Aminov

You can optimize your solution with the bitwise operation! Complexity: O(2^m * n) Here is my solution

Spoiler


using namespace std;
const int N = 1123;
int t[N];
int d[N], cnt[(1 << 18)], w[(1 << 18)];

int bit(int x)
{
    int cnt = 0;
    while(x > 0)
    {
        cnt ++;
        x &= x — 1;
    }
    return cnt;
}
int n, m;
void funk(int n, int m)
{

    int i, j, k;
    char x;
    for(i = 1; i <= n; i ++)
    {
        d[i] = 0;
        for(j = 0; j < m; j ++)
        {
            scanf(" %c", &x);
            d[i] += (x == 'X') * (1 << j);
        }

    }
    int ans = 1e9;
    int s = 0;
    for(i = 0; i < (1 << m); i ++)
    {
        s = 0;
        for(j = 1; j <= n; j ++)
        {
            t[j] = d[j];
        }
        t[1] ^= w[i] & ((1 << m) - 1);
        t[2] ^= i;
        s += cnt[i];
        for(j = 2; j <= n; j ++)
        {
            t[j] ^= (w[t[j - 1]] & ((1 << m) - 1));
            t[j + 1] ^= t[j - 1];
            s += cnt[(t[j - 1])];
        }
        if(t[n] == 0)
            ans = min(ans, s);
    }
    if(ans != 1e9)
    {
        printf("You have to tap %d tiles.\n", ans);
    }
    else
    {
        puts("Damaged billboard.");
    }
}
main() {
    for(int i = 0; i < (1 << 16); i ++)
    {
        for(int j = 0; j < 16; j ++)
        {
            int c = ((i & (1 << j)) != 0);
            c += (j != 0 && ((i & (1 << (j - 1))) != 0));
            c += (j != 15 && ((i & (1 << (j + 1))) != 0));
            c %= 2;
            if(c)
                w[i] ^= (1 << j);
        }
        cnt[i] = bit(i);
    }
    while(cin >> n >> m)
    {
        if(n == 0 && m == 0)
            break;
        funk(n, m);
    }

Try all possibilities for the first row, after that it's easy to see which ones you should switch in the second row (the ones that are still black in the first row), then the same applies for the third row, etc..

Upsolver

We actually solved it using systems of linear equations.

Suppose a_ij is the number of times a tile at row i and column j gets swapped. First of all, a_ij ≤ 1. Then, for each position (i, j) we can get it's final color as (initial_color_ij + a_ij + a_{i - 1, j} + a_{i + 1, j} + a_{i, j - 1} + a_{i, j + 1}) mod 2.

That gives as a system of equations with n·m equations and unknowns. Sure it's not as easy to code, but it gives better time asymptotic.

The system of equations can have many solutions, how do you choose the one that minimizes the number of taps?

Great question!

It turns out, that number of free variables (meaning we can choose any value for them) is not that big (7 for 16x16 matrix). We can search over all possible values for this (at max 7) free values and find other unknowns, then choose one that minimises number of taps.

LeMieux

Can anyone explain the solution for Problem C?

Блог пользователя MikeMirzayanov