Special thanks to Seyaua for help with translation.
Div. 2 A — Vitya in the Countryside
Idea: _XuMuk_.
Preparation: _XuMuk_.
There are four cases that should be carefully considered:
an = 15 — the answer is always DOWN.
an = 0 — the answer is always UP.
If n = 1 — the answer is -1.
If n > 1, then if an–1 > an — answer is DOWN, else UP.
Time Complexity: 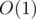 .
.
Div. 2 B — Anatoly and Cockroaches
Idea: _XuMuk_.
Preparation: _XuMuk_.
We can notice that there are only two possible final coloring of cockroaches that satisfy the problem statement: rbrbrb... or brbrbr...
Let’s go through both of these variants.
In the each case let's count the number of red and black cockroaches which are not standing in their places. Let's denote these numbers as x and y. Then it is obvious that the min(x, y) pairs of cockroaches need to be swapped and the rest should be repaint.
In other words, the result for a fixed final coloring is exactly min(x, y) + max(x, y) - min(x, y) = max(x, y). The final answer for the problem is the minimum between the answers for the first and the second colorings.
Time Complexity: 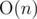 .
.
Div. 1 A — Efim and Strange Grade
Idea: BigBag.
Preparation: BigBag.
One can notice that the closer to the decimal point we round our grade the bigger grade we get. Based on this observation we can easily solve the problem with dynamic programming.
Let dpi be the minimum time required to get a carry to the (i - 1)-th position.
Let's denote our grade as a, and let ai be the (i)-th digit of the a. There are three cases:
If ai ≥ 5, then dpi = 1.
If ai < 4, then dpi = inf (it means, that we cann't get a carry to the (i - 1)-th position).
If ai = 4, then dpi = 1 + dpi + 1.
After computing dp, we need to find the minimum pos such that dppos ≤ t. So, after that we know the position where we should round our grade.
Now we only need to carefully add 1 to the number formed by the prefix that contains pos elements of the original grade.
Time Complexity: 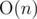 .
.
Div. 1 B — Alyona and Copiers
Idea: _XuMuk_.
Preparation: BigBag.
Deleted
div. 1 C — Sasha and Array
Idea: BigBag.
Preparation: BigBag.
Let's denote 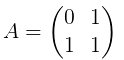
Let's recall how we can quickly find n-th Fibonacci number. To do this we need to find a matrix product  .
.
In order to solve our problem let's create the following segments tree: in each leaf which corresponds to the element i we will store a vector 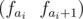 and in all other nodes we will store the sums of all the vectors that correspond to a given segment.
and in all other nodes we will store the sums of all the vectors that correspond to a given segment.
Now, to perform the first request we should multiply all the vectors in a segment [l..r] by 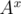 and to get an answer to the second request we have to find a sum in a segment [l..r].
and to get an answer to the second request we have to find a sum in a segment [l..r].
Time Complexity: 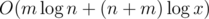 .
.
Div. 1 D — Andrew and Chemistry
Idea: _XuMuk_.
Preparation: BigBag.
Let’s first figure out how we can solve the problem in  time.
time.
Let’s pick a vertex we’re going to add an edge to and make this vertex the root of the tree. For each vertex vi we’re going to assign a label a[vi] (some number). The way we assign labels is the following: if the two given vertices have the same subtrees they’re going to get the same labels, but if the subtrees are different then the labels for these vertices are going to be different as well.
We can do such labeling in a following way: let’s create a map<vector<int>, int> m (the maximum degree for a vertex is 4, but let’s assume that the length of the vector is always equal to 4). Let m[{x, y, z, w}] be a label for a vertex which has children with the labels x, y, z, w. Let’s note that the vector {x, y, z, w} should be sorted to avoid duplications, also if the number of children is less than 4 then we’ll store - 1’s for the missing children (to make the length of a vector always equal to 4). Let’s understand how we can compute the value for the label for the vertex v. Let’s recursively compute the labels for its children: v1, v2, v3, v4.
Now, if m.count({a[v1], a[v2], a[v3], a[v4]}) then we use the corresponding value. Otherwise, we use the first unused number: m[{a[v1], a[v2], a[v3], a[v4]}]=cnt++.
Now, let’s pick another vertex which we’re going to add an edge to. Again, let’s make it the root of the tree and set the labels without zeroing out our counter cnt. Now, let’s do the same operation for all the other possible roots (vertices, n times). Now, one can see that if the two roots have the same labels, then the trees which can be obtained by adding an edge to these roots, are exactly the same. Thus, we only need to count the amount of roots with different labels. Also, we should keep in mind that if a degree for a vertex is already 4 it’s impossible to add an edge to it.
The solution described above has the time complexity  , because we consider n rooted trees and in the each tree we iterate through all the vertices (n), but each label update takes
, because we consider n rooted trees and in the each tree we iterate through all the vertices (n), but each label update takes  .
.
Let’s speed up this solution to  .
.
Let b be an array where b[vi] is a label in a vertex vi if we make this vertex the root of the tree. Then the answer to the problem is the number of different numbers in the array b. Let’s root the tree in a vertex root and compute the values a[vi]. Then b[root] = a[root] and all the other values for b[vi] we can get by pushing the information from the top of the tree to the bottom.
Time complexity: 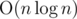 .
.
Div. 1 E — Matvey's Birthday
Idea: BigBag.
Preparation: BigBag, GlebsHP.
Let’s prove that the distance between any two vertices is no more than MaxDist = 2·sigma - 1, where sigma is the size of the alphabet. Let’s consider one of the shortest paths from the position i to the position j. One can see that in this path each letter ch occurs no more than two times (otherwise you could have skipped the third occurrence by jumping from the first occurrence to the last which gives us a shorter path). Thus, the total amount of letters in the path is no more than 2·sigma which means that the length of the path is no more than 2·sigma - 1.
Let disti, c be the distance from the position i to some position j where sj = c. These numbers can be obtained from simulating bfs for each letter c. We can simulate bfs in O(n·sigma2) (let’s leave this as an exercise to the reader).
Let dist(i, j) be the distance between positions i and j. Let’s figure out how we can find dist(i, j) using precomputed values disti, c.
There are two different cases:
The optimal path goes through the edges of the first type only. In this case the distance is equal to
 .
.The optimal path has at least one edge of the second type. We can assume that it was a jump between two letters c. Then, in this case the distance is disti, c + 1 + distc, j.
Adding these two cases up we get: 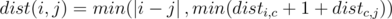 .
.
Let’s iterate over the possible values for the first position i = 1..n. Let’s compute the distance for all such j, where 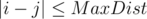 by the above formula.
by the above formula.
Now, for a given i we have to find max(dist(i, j)) for 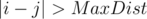 . In this case dist(i, j) = min(disti, c + 1 + distc, j).
. In this case dist(i, j) = min(disti, c + 1 + distc, j).
Let’s compute one additional number distc1, c2 — the minimal distance between positions i and j where si = c1 and sj = c2. This can be easily done using disti, c.
One can notice that distsj, c ≤ distj, c ≤ distsj, c + 1. It means that for every position j we can compute a mask maskj with sigma bits where i-th bit is equal to distj, c - distsj, c. Thus, we can compute the distance using only sj and maskj.
I.e. now distj, c = distsj, c + maskj, c.
Let cnt be an array where cntc, mask is the number of such j where 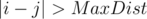 , sj = c and maskj = mask. Now, instead of iterating over j for a given i we can iterate over (c, mask) and if cntc, mask ≠ 0 we’ll be updating the answer.
, sj = c and maskj = mask. Now, instead of iterating over j for a given i we can iterate over (c, mask) and if cntc, mask ≠ 0 we’ll be updating the answer.
Time complexity: 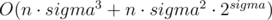 .
.










Editorial Div 1 C: "Now, to perform the first request we should multiply all the vectors in a segment [l..r] by and to get an answer to the second request we have to find a sum in a segment [l..r]."
Care to elaborate this please ? How to multiply all the vectors in segment [l..r] keeping time complexity low?
You need to use segment trees with lazy propagation, you can read about them here.
http://mirror.codeforces.com/blog/entry/15890
DIV 1C:
I don't know much about Fibonacci number's properties. For this reason I can't understand the following statement.
to perform the first request we should multiply all the vectors in a segment [l..r] by A^x
Can anyone please explain how the idea works? or any resource to learn this kinds of stuffs. Thanks in Advance.
Here
Div.2 B: Please, explain, how we can get answer 3 for this test step by step: rbbbrbrrbrrbb?
swap 3rd 'b' with 8th 'r' resulting in answer=1 swap 9th and 10th resulting in answer=2 and color last one with 'r' resulting in 3
Thanks, I got it. Unfortunately, I didn't understand statement right, considering that we can swap only adjacent chars.
I also misunderstood the same.
For some reason my solution for Div1D failed on test case 26 and I have no idea why it failed. Can someone help take a look at it please?
http://mirror.codeforces.com/contest/718/submission/20885319
UPD: Tried out some other implementation and this somehow worked... http://mirror.codeforces.com/contest/718/submission/20890359
Now I am even more confused. Why does using the mapped value of the vector as a key DOES NOT work while using the vector as a key work? I suppose they are the same, unless this somehow cheesed some test cases.
I don't know if this is related, but isn't
m1[hh[now]]=m1.size();undefined behavior? You're using the value of size() which might be modified by the indexing operation.I am not sure about this either, yet from my prior experience this returns the size value after the insert action is done.
I just tried to replaced those affects by a time value, yet it seems that something went wrong... I shall update after I get back to my own computer and run it with a debugger.
UPD: Okay, I just found magic. On line 47 there was an extra semicolon behind the if condition causing problems, so the hashed values are not necessarily correct, and the second version seem to cheesed through this flaw and made an shameful AC...
Now the mystery remains on what black magic made the first code survived that many test case and the second one got an AC.
Was anyone able to solve div 1 C in Java , I tried the same approach given in the editorial but it's exceeding time limit in test case 11 . What might be the possible reasons Submission
how to speed up my div2E solution? http://mirror.codeforces.com/contest/719/submission/20888238 basically: i precompute all powers of 2 of the transformation matrix so, for example i want to get A^18, i just do A^16 * A^2 then for each node in the segment tree, i store the sum of the transformation matrix, so if i want to get the fibonacci sum of a node, i just multiply (1,1) with the matrix stored in the node, however im getting TLE, while i see the editorial has a similar approach (it stores the fibonacci matrix instead of the transformation matrix)
It appears that 2*2 vectors are too slow for the task... I don't know the reason though — I just somehow cheesed out a solution after hours of trial and error, and I am still quite lost.
Just FYI, here are my codes:
http://mirror.codeforces.com/contest/719/submission/20889881
Uses 2*2 vectors for computation, TLE on test case 10.
http://mirror.codeforces.com/contest/718/submission/20890001
Uses two variables instead, clutches the TL 4926/5000
As a side note, when I didn't fixed the overflow problem, the vector implementation failed at test case 8 ~150ms, while the two variable implementation only used 15ms.
My solution uses transformation matrix gets TLE on test 11 . Can you say how can i optimise it. http://mirror.codeforces.com/contest/718/submission/20890160
Can you explain your method of two variables.
Again, I still don't fully understand how my optimization worked, so I am as lost as you right now, and I can't guarantee the correctness of my suggestions. If somebody has a clear picture please kindly lend some help. =]
Try not to use long long everywhere. Although that helps out a lot with handling overflow, but they are very slow, so use them only when you have to.
You are parsing the full matrix. Although it does not affect the theoretical time complexity, but considering that long long has a slower R/W speed and you are trying to cheese through the time limit, parsing the full matrix seems to be pretty slow.
Thanks for reply.BTW can you explain a bit your method of two variables.
Instead of keeping the whole matrix, I just keep Fn and Fn-1, that means I am only keeping half of the matrix.
You can precompute even more. You can split the exponent E into 4 parts, let's say E = a + 216b + 232c + 248d, where each a, b, c, d < 216. Then you precompute 4 tables of the forms:
Then to get ME you make 4 table lookups and three matrix multiplications.
Moreover, using e.g. Sage we can check the order of the matrix:
So actually we can reduce the exponent modulo 2000000016 < 231. Therefore it is enough to compute 2 tables instead of 4 and we can compute ME for any E with only 1 matrix multiplication.
20869723 see Exper class.
I implemented your idea using a modulus of 216 also I have changed most of my long variables to ints (except in multiplication) but still I am getting TLE at test 17 . Is it due to the creation of matrices . Submission
whats sage?
It is a python-based mathematical system. http://www.sagemath.org/
so your solution is basically decompose A^x to base 2^16, right?
Decompose the exponent (x in Ax) to base 216, yes.
Can you please have a look at my solution in the comment below?
i tried your method all night, still cant find my bug http://mirror.codeforces.com/contest/719/submission/20909753. i just added the extra precomputing method and changed the "dnc" fucntion to return a^x. i beleive the rest are correct, would you take a look please?
First, you store M2i in pp array. So pp[0] = M1, not M0. Then pp[1] = M2, etc. In the loop you then use x = 0.
Fixing this I still get TL in 18th test.
Then I changed vectors matrix to structure and it passed in 1.5 seconds: 20923387
Editorial for problem D skipped the difficult part as this comment.
Sorry, I've already answered for this question in Russian, but not in English.
Let's pick two vertices v1 and v2 we're going to add edges. It's obvious, that if b[v1] = b[v2], then these trees are isomorphic. Now I'm going to prove that if b[v1] ≠ b[v2], then these trees aren't isomorphic.
Assume the contrary, i.e. that trees are still isomorphic. It means that the we can pick some vertex v3 with degree 1 (let's the only edge leads to the vertex to) in such way, that these rooted trees (at the vertices v1 and to respectively) will be equal. Now let's delete from the first tree edge (v1 - new) and from the second — (v3 - new) (after this operation the trees are still equal).
Note, that the first tree is our intial tree, and the second — intial tree with edge (v3 - to) changed to the edge (v2 - new). Let's define our intial graph as G. Now we have that G = G - (v3 - to) + (v2 - new). It means that after deleting an edge (v3 - to) the following will be true: b[to] = b[v2]. If now we add the edge (v2 - new), then by the assuming the following will be also true: b[v1] = b[to]. So we get that b[v1] = b[v2]. Contradiction.
I'm having difficulty understanding this part:
Why b[to] = b[v2]? Isn't this statement equivalent to what you were trying to prove in the first place?
I think you are right.
The statement is equivalent to (G - (v3 - to)) + (v3 - to) = (G - (v3 - to)) + (v2 - new), which is the same as the original statement.
However, we can obverse that |G - (v3 - to)| = |G| - 1. So induction completes the proof.
Could you explain your idea in div.1B? Although it is incorrect, I am still curious about your approach, as it may be special and I can learn something from it. Furthermore, it can help to fix your nistakes. So I think sharing this approach should be appreciated :)
I think the solution should be posted, and the problem put back on the website with the updated statement so people can still work on it.
In div2 C,I am not getting the first statement."One can notice that the closer to the decimal point we round our grade the bigger grade we get." Can anyone please explain it?
In every move we can round it off to any decimal point (wherever possible) . Hence, it makes sense not to waste moves at the far off ends (right end ) and instead make it closer to the decimal point as closer the number the decimal point the bigger is the number. e.g 1.225116 should be rounded to 1.23 and not 1.22512 in one move. That's why after calculating the dp array we take the leftmost dp[i] that is less than or equal to t.
my solution for div 2 problem B failed on test #7 , the reason of which i dont know. my solution procedure is same as of editorial. here's my code , please tell me what mistake i made
http://mirror.codeforces.com/contest/719/submission/20898465
You are changing the value of s[0] in every loop.
Someone please help me in optimising this code ,getting TLE on test 11 , initailly i was passing the complete transformation matrix and getting TLE on test 11 , then tried optimising it as mentioned in editorial by passing fibonacci numbers and then furthur by using ints ,still to fail on the same case.
http://mirror.codeforces.com/contest/718/submission/20898639
Someone please help!!
You are doing exponentiation on each lazy push which yields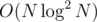 complexity (because exponentiation is
complexity (because exponentiation is  ). You have two options:
). You have two options:
optimize exponentiation as I mentioned before here so it becomes constant time (one or three multiplications);
or perform exponentiation immediately on query and store matrices in the "lazy" array.
can you explain a bit more the second method please?
We use matrix as a lazy tag(which is [0 1;1 1]^x).When we download the lazy tag, we just need to multiply it lazy tag with its father's lazy tag and change its father's lazy tag to [1 0;0 1](which is equal to E). Also we should record [f[a[n]-1] f[a[n]]] this matrix at each node. So when we do the query operation, we just need to calculate the sum of f[a[n]]. And when we do the change operation, we just need to calculate the [0 1;1 1]^x first, and then use it as a lazy tag.
THanks for your help but i am now caught in test case 28 here is my submission http://mirror.codeforces.com/contest/718/submission/20912507
i used fast input can you suggest more optimisation please?
In Div 2 C, I simply found the first digit after the dot which is >= 5 and then updated the marks. No dp, simple implementation. http://mirror.codeforces.com/contest/719/submission/20880366
Then b[root] = a[root] and all the other values for b[vi] we can get by pushing the information from the top of the tree to the bottom
What information specifically ? and how can we obtain values of b[i] for i != root in nlogn
So what we are doing are essentially similar to tree dp.
First you fix a root, run a dfs to get a[]. Since the the root is currently being considered, b[root] = a[root]. For other points, we have to move the root from a point to point. This involves three actions, assume that we are moving from node u(the current node) to node v(the new node):
This transfer process gets run by O(n) times, so that's O(NlogN) in total.
My code: http://mirror.codeforces.com/contest/718/submission/20890359
Refer to the "move" function for updating the root (i.e. pushing the information).
Div 2C/Div 1A (Efim and Grades) : Alternate Approach
Find the position of Decimal '.' and say it is dec . Now iterate from dec to end of the grade( stored as string) until we find a position where the digit is greater than or equal to '5' .
If no such position exits then print the string as it is. Else, reverse iterate from that position towards dec until we exhaust our seconds or the digit at consideration is not '4' . Round the grade at the position we stopped.
If we reached dec then the output should should be an integer, 1 greater than the integer part of input. That step is a well known operation.
Here's my code for further reference :
http://mirror.codeforces.com/contest/719/submission/20860189
same greedy approach here! 20863325
I want to solve (div.1B / div.2D)! Where can I submit it? I'm waiting for 3 days!
AFAIK you can't submit it, you can share your approach though — many are eager to know the correct solution as the greedy solution has a flaw.
My approach for that problem had 2 parts. The first part was finding the time where each machine starts working, the second part was finding the time for each query via binary search.
This solution has complexity O(M * NlogK), where K is the maximum time (1018 for one machine with ti = 109 and 109 sheets of paper). Certainly this solution wouldn't fit into the given time limit, but I'd still want to know whether it's correct or not.
UPDATE: As noted below, and as discussed previously, this solution is wrong.
This is the greedy variant, which most people assumed is correct (and the task authors too). See discussion why it's incorrect.
In short, "There will be always at least one paper available to work with" is wrong. Test:
Answer is 7 (greedy answer is 8).
Ahhhhh, I see! Thanks.
how to implement the div1 A using DP? I mean how to code the logic
Check this out 20928655
Div 1 A, alternate solution. Input number as a string, let's call it str. Scan str from the character after decimal point to end of number. Find the first character that is greater than or equal to 5. The position before this is where rounding off should be done. Eg — If no=3.13 3 523419, rounding should be done at the '3' in bold.
Now, multiple round-offs will be possible only if there is a chain of '4's before the first character >= 5. Eg — If no is 12.3444 4 5, then after one second it can be made 12.3444 5 , after another second it will become 12.344 5 until either time runs out, we exhaust all '4's or reach the decimal point.
After this step, wherever we reach, let's mark that index as 'x'. Now we need to round off from position x. To round off, keep moving backwards towards the beginning of number, increasing each '9' to '0'. Increment and break as soon as a non-'9' character is encountered. If beginning of str is reached, print 1 followed by modified number, else print modified number.
In Div1 C, This submission allocates only O(2*N) space for segment tree and also passes the system testing. Don't we need to allot O(4*N) space for segment tree? Solution
Imagine a function maxNode(x) of the number of nodes needed for segment tree, the first thing is that maxNode(x) is increasing, which is a little bit intuitive. So the next thing is the if N (the number of nodes) is a power of two the tree is perfectly balanced and the number of nodes in the segment tree will be exactly 2N - 1 so if MAXN is a power of two and is greater than any N that will be used i will be safe to use 2 * MAXN of size in the segment tree, since for any N < = MAXN the following expression will hold maxNode(N) < = maxNode(MAXN) = 2 * MAXN - 1. So know you know how to save memory ;)
Edit: As noted in the comments, in this explanation maxNode(x) should be the maximum index used (hence the size of the array it needs) in the "traditional" naive recursive segment tree used in the submission posted above.
Got it, thanks!
Actually, if F[N] is the number of nodes needed to construct a segment tree for N elements, then the equality F[N] = 2N - 1 holds for every N, not only for powers of two.
To prove it we can note that F[1] = 1 and F[2] = 3. The rest can be done by induction.
So, no matter the value of N, you can always go safe by setting the size of the tree to be 2N.
UPDATE: As noted by ffao below, while the tree will have size 2N - 1, there will be out of bounds violation when trying to access some children. Moreover, you won't be able to access all children intuitively by going to nodes 2i and 2i + 1. In other words, if you wanna be safe, always use powers of 2 as sizes. I always used powers of 2, so I never had these problems, but I'd never stopped to consider why we should use powers of 2 for the size.
Yeah it is true. I was referring to maxNode needed for maximum index used by the specific implementation he asked. Since what you demonstrate there doesn't prove why the posted implementation uses 2*N space.
To stress the point, "it is always safe to set tree size to 2N" is false, because even if your tree only uses 2N-1 nodes, indexing them in the intuitive way causes some of them to receive indices outside the 2N limit.
It's not false. I don't know what you mean by indexing them the intuitive way, but intuitive to me is indexing them from 1 to 2N - 1, such that the root is 1 and children of node i are 2i and 2i + 1, and that's clearly valid with an array of size 2N.
And here we have confirmation bias at its finest. When confronted with the opposite opinion, humans tend to hole up and defend their opinion to the death instead of, you know, trying to evaluate if the other person has any merit in what they're saying.
Luckily, unlike political stances this is an exact science, and I can prove you wrong.
Did you try doing the same thing as you did with 8 by listing the tree nodes, but with a number that isn't a power of 2, such as 18? I didn't think so, or you'd have seen the last index goes beyond 2*N.
Did you try submitting a solution that has an array of size 2*N? I also didn't think so, and I even did your work for you, here it is: 20952741. Look at that, runtime error, what a surprise!
Well, I think I gotta apologize... now I feel like an idiot.
Indeed, the tree will have 2N - 1 nodes, but not all the children will be at 2i and 2i + 1. For example, children of node 24 (range [10, 11]) will be at indices 34 and 35.
Sorry for being a jerk.
I might have overreacted a bit as well, I get a bit rattled when someone doesn't consider what new information might mean. So sorry about that, too.
This blog has a tutorial about how to implement a O(2*N) memory space segment tree in a very clean, abstracted way.
http://mirror.codeforces.com/blog/entry/18051
Why would we need O(4 * N) space for a segment tree? Consider this very simple example of what range each node of the tree represents, for a tree with 8 nodes.
T1 = [1, 8] T2 = [1, 4] T3 = [5, 8] T4 = [1, 2] T5 = [3, 4] T6 = [5, 6] T7 = [7, 8] T8 = [1, 1] T9 = [2, 2] T10 = [3, 3] T11 = [4, 4] T12 = [5, 5] T13 = [6, 6] T14 = [7, 7] T15 = [8, 8]
The same applies for other values as well. I like to work with powers of 2 for size, so I always allocate double the nearest power of 2 for segment trees.
Could someone help me why this[submission:20981794] TLE on test16?I thought this code time complexity was O(mlogn+(n+m)logx).so sad...
In Problem DIV2-B (Div. 2 B — Anatoly and Cockroaches)
I am getting a run-time error on test case 5. I have debugged the code, and don't see any reason for the error. Could it be because I am creating new strings?
Could anyone please help me out with this? Cannot understand why this is happening.
My code — code
You're creating empty strings and then trying to access indices from them. You should resize them or copy the content from the original string.
Here's the corrected code -> 20990040
Thanks a lot Tenshi!. Just a small doubt. My code then, shouldn't have worked on any test case, right? Why is it working for test cases 1-4?
I don't have much knowledge about compilers, but I'll try to explain what I think might be making your program work for small test cases.
s1ands2, you also declare 7 integers (28 bytes).s1and 13 bytes froms2, which your program already allocated memory for. You're overwriting other variables, I think.s1ands2to create stringsnew1andnew2, but in this step, you usepush_back, so your program allocates new memory and it works.new1andnew2, your program gives correct answer.I got it! Thankyou so much :)
Div. 1 C can be solved by sqrt decomposition. My solution passed by a tiny bit, and I had to cut down on the recalculation of fib(x) when answering queries of the second first type.
TLE Submission: 21113527 AC Submission: 21115015
Div1, C. Getting WA on TC 11 . I've checked the code like 50 times but not able to find mistake. Please help :O Code
Div 1C, I implemented a segment tree of nodes made of matrices and calculating fibonacci numbers by matrix exponentiation in log n (Also Lazy Propogation). The complexity must be o(n*log(max(ai)) + m*log(m)). But I've been getting a timeout on TC10. Can someone help why it is timing out? My Code