vepifanov's blog

Intel Code Challenge Elimination Round (div.1 + div.2 combined) editorial
By vepifanov, 8 years ago, In Russian
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
  • Vote: I like it
  • +60
  • Vote: I do not like it

Comments Comments (31)
| Write comment?
»
8 years ago, # |
← Rev. 4   Vote: I like it +51 Vote: I do not like it

(Probably) easier method for last part of F, as k ≤ 40 :(

While moving right pointers, we can put the system of questions apart and instead we want to check if there is a conflict between the newly added element and any old element we added before (i.e. those two cannot appear together in same time). Let ki and pi be the length of cycle of position of the element in cycle of element i. Two element i and j conflicts iff there exists integer d so that d divides both ki and kj and pi mod d  ≠  pj mod d. As ki is so small, we can just enum all possible d and record the only possible value pd (if there are two values for same d at the same time, some pair of elements conflict and bad things happen). This algorithm is O(N log f(k)), where f(k) is the maximum number of factor of integers from 1 to k.

I wonder if you reduced the difficulty of this problem as if k ≤ 200000 this solution will TLE, and also your solution seems more beautiful than mine :(

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    I think this part could be done in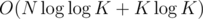 since it is enough to check contradiction with k = pa1·...·pam for each pai.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If k<=200000 wouldn't handling the lcm in the sparse table become a fierce task for the author's solution?

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    How do you show that if there is not pairwise conflict, then there is a solution?

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    If k ≤ 200000 wouldn't the LCM get insanely big (requiring big int) for editorial solution? Is there a trick I'm missing for this?

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Edit: I was wrong. In D you can have O(n*(logn+log10^9)) if you keep a priority queue and a hash set of the same values: In each iteration get the max Y_i from the priority queue in O(log(n)) and check for the min value one by one from the hash set in O(log10^9)

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain the C problem's solution, I don't understand the editorial's solution.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it +4 Vote: I do not like it

    The main idea behind the solution is actually we can process the queries offline . That is instead of traversing from i=1 to n and deleting every element we can actually revert the task and start from i=n to 1 and insert the element into its corresponding set. Everything is 1-indexed :)

    Like the example n=4 , a={1,3,2,5} and p={3,4,1,2}; We have a boolean array ok to check if certain element is in set or not. Also keep a sum(long) array to keep track of sums of a set Initally all elements have parent[i]=i;

    we start from i=4 and intially we have all sets as null so current ans=0 ( beacuse at last all elements are going to be deleted ). Now print 0 and let x=p[4] so update sum[x]=a[x] , as in our case a[2]=3 . we check both left and right of 'x' and we can see that neither 1 nor 3 is visited so simply find parent of 'x' which is 2 itself, so ans is updated to be max(0,s[parent[x]]); =>ans=3 and mark visited[2]=true; Next we have i=3 and p[3]=1. So we again check for left and right . In our case we only check for right side(1-indexing) so 2 is visited so we merge both set having element 2 and set having single elememt in 1 in such a manner so that the parent of the resulting set has suppose index as "parent_index" then sum[parent_index]=sum_of_all_elements_in_set; next we update our ans and as its either max sum from merging our current set or from previously merged sets and then we mark the element we processed as visited.

    Continue for rest elements and Bamm its Accepted.

    FatalEagle 's code in c++ : http://mirror.codeforces.com/contest/722/submission/210747661

    my submission in Java : http://mirror.codeforces.com/contest/722/submission/21097209

    → Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it +40 Vote: I do not like it

There is a simple O(S * K)(where S is total length of all sequences) solution for F. The idea is as follows:

Let's assume that we have a fixed subsegment [L, R] of the given sequences and a fixed number x.
Let pos(x, i) be the position of the number x in the i-th sequence and len(i) be the length of the i-th sequence. Then the [L, R] segment will be filled with x at some point if and only if:
- Each sequence contains x
- for all L <= i < j <= R, (pos(x, i) - pos(x, j)) mod gcd(len(i), len(j)) == 0
The first condition is trivial. The second one follows from the Chinese remainder theorem.
It implies that if len(i) == len(j) then pos(x, i) == pos(x, j). Thus we have at most one unique position of the element for all sequences of a specific length in a valid segment.

This criterion leads us to a solution that uses two pointers. Let's fix the value of the element. We need to keep track of the position of this element for each distinct length of a sequence. When we try to expand the segment by one to the right, we check that there is no conflict (by iterating over all distinct lengths (from 1 to K) and testing it with the position and length we're about to add) and add a new position and length if we can. When we move the left border, we just delete the corresponding position and length.

A few details: gcd's can be precomputed. We need to take into account only positions of those sequences that actually contain any fixed element.

Here is my code.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    "For all L <= i < j <= R, (pos(x, i) - pos(x, j)) mod gcd(len(i), len(j)) == 0"

    Please explain this in more detail. I mean, if we know that

    And for all 1 ≤ i < j ≤ 3,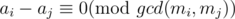 , how can we prove that there exists an x which satisfies all these three equation? Thank you.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it +5 Vote: I do not like it

      This criterion clearly works for two equations (it follows from the fact that any linear combination of two integers with arbitrary integer coefficients is divisible by their gcd. Moreover, the gcd can be represented as a linear combination of these numbers). For three equation we can go like this:

      1. Let's solve the first two. The solution is x = x0 (mod lcm(m1, m2)). Now let's show that for the system of two equations x = x0 (mod lcm(m1, m2)) and x = a3 (mod m3) the initial criterion holds true.

      2. Let's consider an arbitrary prime p. Let p^a, p^b and p^c be the maximum powers of p that divide m1, m2 and m3 respectively. The initial criterion means that
        x0 - a3 = 0 (mod p^min(a, c)) and x0 - a3 = 0 (mod p^min(b, c)). The power of p in lcm(m1, m2) is max(a, b). Thus, its power is min(max(a, b), c) in gcd(lcm(m1, m2), m3). The two equations above imply that
        x0 - a3 = 0 (mod p^min(max(a, b), c)).

      3. Now let's use the fact that if a | x, b | x, a and b are coprime then ab | x. It allows us to prove 2. for all powers of primes and conclude that it's true for
        gcd(lcm(m1, m2), m3).

      We've just shown that we can reduce the number of equations by one and the criterion stays true. If we have more than 3 equations, we can use induction.

      → Reply
»
8 years ago, # |
  Vote: I like it +29 Vote: I do not like it

Problem D: It should be choose maximum element that does not exist in Y from yi/2, ...., 1. Choosing minimum element gives WA on 1, 2, 9, 17.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +9 Vote: I do not like it

    Yes, that's what I was thinking too. I tried solving it by choosing the minimum number and it doesn't pass pretest 3.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Choosing minimum element also works longer :)

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thank you for pointing that, it should be fixed now.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Hey, i found another solution for problem C, i'm using segment tree, where the idea is just like the problem GSS or GSS3 in S.P.O.J, where each time an element is destroyed, i change its value to -1E14-10000000 because maximum total sum of an array couldn't be exceed 1E9*1E5=1E14.

The program might be complicated and hard to code, but hey, it's good to share an idea right :)

my code

GSS3 — spoj

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it -10 Vote: I do not like it

O(n) solution for problem C : http://mirror.codeforces.com/contest/722/submission/21107463

EDIT : Sorry, the link I posted was wrong. Now, it is correct.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +5 Vote: I do not like it

    As far as I can tell, this uses a segment tree with one update and one get operation for each input number. This is O(n log n).

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone explain solution to problem D ?

→ Reply
»
8 years ago, # |
  Vote: I like it +10 Vote: I do not like it

In problem F:

The editorial says "For each such subsegment we can find the solution of the corresponding system using O(1) time by solving a system consisting of two equations obtained from each of the halves of this subsegment. We can solve a system consisting of two equations using the Chinese remainder theorem.", So how can we solve Chinese remainder theorem in O(1) instead of O(logn)

I think this should add another log in sparse table complexity which makes complexity n*log^2(n)

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Yes, you are right. But it will actually be log 10^16, since we need to find the inverse number (using f.e. extended gcd algorithm).

    → Reply
»
8 years ago, # |
  Vote: I like it +8 Vote: I do not like it

O(N) solution for problem C

C++ code : http://mirror.codeforces.com/contest/722/submission/21163148

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Thanks a lot,

    Could you briefly explain the below step of your code:

    if(other_end[pos-1]!=0) { l = other_end[pos-1]; sum += seg[l]; } if(other_end[pos+1]!=0) { sum += seg[pos+1]; r = other_end[pos+1]; }

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 3   Vote: I like it +3 Vote: I do not like it
      • seg[i] : Segment sum of the segment starting at index 'i'
      • other_end[i] : Starting/Ending index of the segment Ending/Starting at index 'i'
      • res : Maximum segment sum found until now
      • l : Starting index of segment of current element to be inserted
      • r : Ending index of segment of current element to be inserted
      • sum : Segment sum of the segment in which current element is inserted

      While inserting the current element into the array at 'pos', we need to merge it with the neighboring segments if any.

      Initially assume there are no segments adjacent to 'pos'.
  l = r = pos
  sum = A[pos]

if(any segment 'S' ending at 'pos-1' exists) 
   update 'l' with starting index of 'S'
   sum += segment sum of 'S'

if(any segment 'S' starting at 'pos+1' exists)
   sum += segment sum of 'S'
   update 'r' with ending index of 'S'
   
Update the segment sum of the new segment [l, r] in the 'seg' array
Update the Starting/Ending index of this segment in 'other_end' array
Check if 'sum' is greater than 'res' and update 'res' accordingly
      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can you give a proof that greedy algorithm for problem D is optimal?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    because any number can be DIRECTLY derived from only one number. This obviously means that set of numbers, that can be derived from number X consists of X itself and sum of sets that can be derived from 2*X and from 2*X+1

    So:

    If X can be derived from Y then SET_CAN_BE_DERIVED_FROM(Y) includes SET_CAN_BE_DERIVED_FROM(X)

    else if Y can be derived from X then SET_CAN_BE_DERIVED_FROM(X) includes SET_CAN_BE_DERIVED_FROM(Y)

    else SET_CAN_BE_DERIVED_FROM(X) and SET_CAN_BE_DERIVED_FROM(Y) DO NOT INTERSECT

    → Reply
»
8 years ago, # |
  Vote: I like it +1 Vote: I do not like it

In problem E's solution, maybe the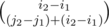 has been written upside down. Sorry for my bad English.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Also in problem E's solution,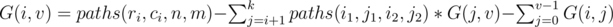 is wrong, the paths(i1, j1, i2, j2) should be paths(ri, ci, rj, cj).

    And "when the j is equal to the number of v-th anomaly from the end on this path" should be "v+1-th".

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What does the second statement in E mean? How is P1*Q1^-1 = P*Q? Shouldn't it be P1*Q1^-1=P*Q^-1(mod 1e9+7)?

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I wrote code for prob E in c++ and java. Exact same codes.

AC in c++. Code

TLE in java. Code. !

Can anyone suggest something to improve java code. I've already used Fast io.

→ Reply