
Добро пожаловать на 2016-2017 CT S03E05: Codeforces Trainings Season 3 Episode 5 (2016 Stanford Local Programming Contest, Extended). Продолжительность тренировки — 4 часа 30 минут. Тренировка открыта как для команд, так и для индивидуальных участников. После ее окончания вы можете дорешивать задачи тренировки или поучаствовать в ней виртуально, если не смогли принять участие одновременно со всеми. Пожалуйста, участвуйте в тренировке честно.
Перейдите в раздел Тренировки для регистрации и участия.
Ориентировочный старт: 5 октября 2016 г., 16:10 (Московское время).
Так как это тренировка, то возможно набор задач будет расширен, если для значительного количества участников он окажется простым.
Условия задач будут на английском языке, ведь мы же готовимся к ACM-ICPC!
Удачи!











Aha, a nice try! This is very creative.
He forgot to append '\n' character. That is why the teacher is angry.
Wuu..It should be printf("I will not forget to append '\\n'.\n").
I'm soory, but '\n' doesn't work!
Nice try :3
How to view solution of other users in Gym contest which I haven't solved ?
How to solve A, H and J?
In problem A, we're asked only the smallest 100 combinations in the worst case, so we can keep track of the smallest k combinations we've seen so far in an array, and whenever the array exceeds k (after sorting) we remove elements from the back.
PS: The technique used in this problem is known as Beam Search, and is widely used in optimization problems.
H: Let's compute the area of the polygon using pseudoscalar product (not sure if this is the right term in English, in 2D it is equal to x1y2 - x2y1). To do that, we just sum up all the oriented areas of triangles (ai, ai + 1, (0, 0)). Note that if we reverse the order, the area will be exactly the opposite. That is why, we can conclude the answer from the sign of the area computed this way.
The term is 'cross product'.
H: For any point X in the polygon, the sum of the signed angles PiXPi + 1 is either 2π, or - 2π, depending on the polygon's orientation. From outside the polygon, the sum is 0.
So all we need to do is find a point in the polygon. I took the midpoint of a non-vertical edge, perturbed it by a small amount upwards and downwards, and computed the sum for these two points.
J: First sort all points by x-coordinate. Now brute force over all combinations of the minimum and maximum y for the rectangle. For each min-max pair, we can find all rectangles containing n/2+1 points using a two-pointer approach, where the pointers mark the left and right boundaries of the rectangle. When we march the left pointer forwards, we lose some points, so we must march the right pointer forwards as well. Total time is O(n3).
I've been asked several times for the code. Here it is: http://ideone.com/XElevb
Is there any tutorial available?? Thank you in advance
Is there any tutorial available? Thank you in advance
how to solve L?
Can anyone help me with J. Thanks in advance
for each 2 X's --> for each Y --> do binary search
the idea is : you need 2 points( upper-left , lower-right )( 2 X's , 2 Y's )
the 2 X's may be the same and the 2 Y's may be the same
the bruteforce solution is O(n^4) ( bad )
to reduce the complexity a little bit you can try :
every 2 X's and 1 Y : binary search the other Y
this solution is O(n^3 logn) ( good enough to pass )
There is no need to do binary search. If you have sorted array of points between X1 and X2 (which you probably need for binary search as well), you can just try pairs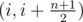 .
.
yes you are right :)
hhhh
in problem G-Ground Defence :
i'm trying to solve it with segment tree ,but how to handle lazy propagation ??
You don't need lazy propagation at all. You're dealing with range updates and point queries.
I get it now , thank you
Just a key observation for not being stuck for ever in problem F: the length of the least path between two points with the same latitude IS NOT the length of the arc of the maximal circle of the sphere that contains both points.
How to solve L and M?
How to solve problem K?
How to solve C?
I compute probabilities for each triple (t, n, nd) (where t — time, n — number of unique cards, nd — number of dublicates, nd < d). But I get expected time 10.414 for the second sample instead of 10.185.
You don't need to trade duplicates immediately.
how to solve B??
Here
Edit :I thought its Ep-03 'B'
I read that too .... Won't it exceed the time limit with given constraints ...?
Your_dad Idea is very Simple.
Think optimally!
This Test Case will help you.
[IN]
1
3 4
0101
1000
0001
[OUT]
9
i solved it too... i just need to confirm the complexity :--> mine is O(n*m) yrs??
How to solve F?)
Oh, I was solving J for one hour because I coded a solution with complexity O(T*N^3) for stress testing in the beginning and then tried to come up with a fast solution. In the end, I just sent the O(T*N^3) and it got accepted in about 100 ms :D
Is this the expected complexity, I thought it would be too slow?
больше не будет тренировок таких?