Hi everyone! Today I want to share some DP tricks and techniques that I have seen from some problems. I think this will be helpful for those who just started doing DP. Sometimes the tutorials are very brief and assumes the reader already understand the technique so it will be hard for people who are new to the technique to understand it.
Note : You should know how to do basic DP before reading the post
DP + Bitmasks
This is actually a very well-known technique and most people should already know this. This trick is usually used when one of the variables have very small constraints that can allow exponential solutions. The classic example is applying it to solve the Travelling Salesman Problem in O(n2·2n) time. We let dp[i][j] be the minimum time needed to visit the vertices in the set denoted by i and ending at vertex j. Note that i will iterate through all possible subsets of the vertices and thus the number of states is O(2n·n). We can go from every state to the next states in O(n) by considering all possible next vertex to go to. Thus, the time complexity is O(2n·n2).
Usually, when doing DP + Bitmasks problems, we store the subsets as an integer from 0 to 2n - 1. How do we know which elements belong to a subset denoted by i? We write i in its binary representation and for each bit j that is 1, the j-th element is included in the set. For example, the set 35 = 1000112 denotes the set {0, 4, 5} (the bits are 0-indexed from left to right). Thus, to test if the j-th element is in the subset denoted by j, we can test if i & (1<<j) is positive. (Why? Recall that (1<<j) is 2j and how the & operator works.)
Now, we look at an example problem : 453B - Little Pony and Harmony Chest
So, the first step is to establish a maximum bound for the bi. We prove that bi < 2ai. Assume otherwise, then we can replace bi with 1 and get a smaller answer (and clearly it preserves the coprime property). Thus, bi < 60. Note that there are 17 primes less than 60, which prompts us to apply dp + bitmask here. Note that for any pair bi, bj with i ≠ j, their set of prime factors must be disjoint since they're coprime.
Now, we let dp[i][j] be the minimum answer one can get by changing the first i elements such that the set of primes used (i.e. the set of prime factors of the numbers b1, b2, ..., bi) is equal to the subset denoted by j. Let f[x] denote the set of prime factors of x. Since bi ≤ 60, we iterate through all possible values of bi, and for a fixed bi, let F = f[bi]. Then, let x be the complement of the set F, i.e. the set of primes not used by bi. We iterate through all subsets of x. (see here for how to iterate through all subsets of a subset x) For each s which is a subset of x, we want dp[i][s|F] = min(dp[i][s|F], dp[i - 1][s] + abs(a[i] - b[i])). This completes the dp. We can reconstruct the solution by storing the position where the dp achieves its minimum value for each state as usual. This solution is enough to pass the time limits.
Here are some other problems that uses bitmask dp :
678E - Another Sith Tournament
Do we really need to visit all the states?
Sometimes, the naive dp solution to a problem might take too long and too much memory. However, sometimes it is worth noting that most of the states can be ignored because they will never be reached and this can reduce your time complexity and memory complexity.
Example Problem : 505C - Mr. Kitayuta, the Treasure Hunter
So, the most direct way of doing dp would be let dp[i][j] be the number of gems Mr. Kitayuta can collect after he jumps to island i, while the length of his last jump is equal to j. Then, the dp transitions are quite obvious, because we only need to test all possible jumps and take the one that yields maximum results. If you have trouble with the naive dp, you can read the original editorial.
However, the naive method is too slow, because it would take O(m2) time and memory. The key observation here is that most of the states will never be visited, more precisiely j can only be in a certain range. These bounds can be obtained by greedily trying to maximize j and minimize j and we can see that their values will always be in the order of  from the initial length of jump. This type of intuition might come in handy to optimize your dp and turn the naive dp into an AC solution.
from the initial length of jump. This type of intuition might come in handy to optimize your dp and turn the naive dp into an AC solution.
Change the object to dp
Example Problem : 559C - Gerald and Giant Chess
This is a classic example. If the board was smaller, say 3000 × 3000, then the normal 2D dp would work. However, the dimensions of the grid is too large here.
Note that the number of blocked cells is not too large though, so we can try to dp on them. Let S be the set of blocked cells. We add the ending cell to S for convenience. We sort S in increasing order of x-coordinate, and break ties by increasing order of y-coordinate. As a result, the ending cell will always be the last element of S.
Now, let dp[i] be the number of ways to reach the i-th blocked cell (assuming it is not blocked). Our goal is to find dp[s], where s = |S|.
Note that since we have sort S by increasing order, the j-th blocked cell will not affect the number of ways to reach the i-th blocked cell if i < j. (There is no path that visits the j-th blocked cell first before visiting the i-th blocked cell)
The number of ways from square (x1, y1) to (x2, y2) without any blocked cells is  . (if x2 > x1, y2 > y1. The case when some two are equal can be handled trivially). Let f(P, Q) denote the number of ways to reach Q from P. We can calculate f(P, Q) in O(1) by precomputing factorials and its inverse like above.
. (if x2 > x1, y2 > y1. The case when some two are equal can be handled trivially). Let f(P, Q) denote the number of ways to reach Q from P. We can calculate f(P, Q) in O(1) by precomputing factorials and its inverse like above.
The base case, dp[1] can be calculated as the number of ways to reach S1 from the starting square. Similarly, we initialize all dp[i] as the number of ways to reach Si from the starting square.
Now, we have to subtract the number of paths that reach some of the blocked cells. Assume we already fixed the values of dp[1], dp[2], ..., dp[i - 1]. For a fix blocked cell Si, we'll do so by dividing the paths into groups according to the first blocked cell it encounters. The number of ways for each possible first blocked cell j is equal to dp[j]·f(Sj, Si), so we can subtract this from dp[i]. Thus, this dp works in O(n2).
Another problem using this idea : 722E - Research Rover
Open and Close Interval Trick
Example Problem : 626F - Group Projects
First, note that the order doesn't matter so we can sort the ai in non-decreasing order. Now, note that every interval's imbalance can be calculated with its largest and smallest value. We start adding the elements to sets from smallest to largest in order. Suppose we're adding the i-th element. Some of the current sets are open, i.e. has a minimum value but is not complete yet (does not have a maximum). Suppose there are j open sets. When we add ai, the sum ai - ai - 1 will contribute to each of the j open sets, so we increase the current imbalance by j(ai - ai - 1).
Let dp[i][j][k] be the number of ways such that when we inserted the first i elements, there are j open sets and the total imbalance till now is k. Now, we see how to do the state transitions. Let v = dp[i - 1][j][k]. We analyze which states involves v.
Firstly, the imbalance of the new state must be val = k + j(ai - ai - 1), as noted above. Now, there are a few cases :
We place the current number ai in its own group : Then, dp[i][j][val] + = v.
We place the current number ai in one of the open groups, but not close it : Then, dp[i][j][val] + = j·v (we choose one of the open groups to add ai.
Open a new group with minimum = ai : Then, dp[i][j + 1][val] + = v.
Close an open group by inserting ai in one of them and close it : Then, dp[i][j - 1][val] + = j·v.
The answer can be found as dp[n][0][0] + dp[n][0][1] + ... + dp[n][0][k].
Related Problems :
"Connected Component" DP
Example Problem : JOI 2016 Open Contest — Skyscrapers
Previously, I've made a blog post here asking for a more detailed solution. With some hints from Reyna, I finally figured it out and I've seen this trick appeared some number of times.
Abridged Statement : Given a1, a2, ..., an, find the number of permutations of these numbers such that |a1 - a2| + |a2 - a3| + ... + |an - 1 - an| ≤ L where L is a given integer.
Constraints : n ≤ 100, L ≤ 1000, ai ≤ 1000
Now, we sort the values ai and add them into the permutation one by one. At each point, we will have some connected components of values (for example it will be something like 2, ?, 1, 5, ?, ?, 3, ?, 4)
Now, suppose we already added ai - 1. We treat the ? as ai and calculate the cost. When we add a new number we increase the values of the ? and update the cost accordingly.
Let dp[i][j][k][l] be the number of ways to insert the first i elements such that :
There are j connected components
The total cost is k (assuming the ? are ai + 1)
l of the ends of the permutations has been filled. (So, 0 ≤ l ≤ 2)
I will not describe the entire state transitions here as it will be very long. If you want the complete transitions you can view the code below, where I commented what each transition means.
Some key points to note :
Each time you add a new element, you have to update the total cost by ai + 1 - ai times the number of filled spaces adjacent to an empty space.
When you add a new element, it can either combine 2 connected components, create a new connected components, or be appended to the front or end of one of the connected components.
A problem that uses this idea can be seen here : 704B - Ant Man
× 2, + 1 trick
This might not be a very common trick, and indeed I've only seen it once and applied it myself once. This is a special case of the "Do we really need to visit all the states" example.
Example 1 : Perfect Permutations, Subtask 4
My solution only works up to Subtask 4. The official solution uses a different method but the point here is to demonstrate this trick.
Abridged Statement : Find the number of permutations of length N with exactly K inversions. (K ≤ N, N ≤ 109, K ≤ 1000 (for subtask 4))
You might be wondering : How can we apply dp when N is as huge as 109? We'll show how to apply it below. The trick is to skip the unused states.
First, we look at how to solve this when N, K are small.
Let dp[i][j] be the number of permutations of length i with j inversions. Then, dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1] + ... + dp[i - 1][j - (i - 1)]. Why? Again we consider the permutation by adding the numbers from 1 to i in this order. When we add the element i, adding it before k of the current elements will increase the number of inversions by k. So, we sum over all possibilities for all 0 ≤ k ≤ i - 1. We can calculate this in O(N2) by sliding window/computing prefix sums.
How do we get read of the N factor and replace it with K instead? We will use the following trick :
Suppose we calculated dp[i][j] for all 0 ≤ j ≤ K. We have already figured out how to calculate dp[i + 1][j] for all 0 ≤ j ≤ K in O(K). The trick here is we can calculate dp[2i][j] from dp[i][j] for all j in O(K2).
How? We will find the number of permutations using 1, 2, ..., n and n + 1, n + 2, ..., 2n and combine them together. Suppose the first permutation has x inversions and the second permutation has y inversions. How will the total number of inversions when we merge them? Clearly, there'll be at least x + y inversions.
Now, we call the numbers from 1 to n small and n + 1 to 2n large. Suppose we already fixed the permutation of the small and large numbers. Thus, we can replace the small numbers with the letter 'S' and large numbers with the letter 'L'. For each L, it increases the number of inversions by the number of Ss at the right of it. Thus, if we want to find the number of ways that this can increase the number of inversions by k, we just have to find the number of unordered tuples of nonnegative integers (a1, a2, ..., an) such that they sum up to k (we can view ai as the number of Ss at the back of the i-th L)
How do we count this value? We'll count the number of such tuples where each element is positive and at most k and the elements sum up to k instead, regardless of its length. This value will be precisely what we want for large enough n because there can be at most k positive elements and thus the length will not exceed n when n > k. We can handle the values for small n with the naive O(n2) dp manually so there's no need to worry about it.
Thus, it remains to count the number of such tuples where each element is positive and at most k and sums up to S = k. Denote this value by f(S, k). We want to find S(k, k). We can derive the recurrence f(S, k) = f(S, k - 1) + f(S - k, k), denoting whether we use k or not in the sum. Thus, we can precompute these values in O(K2).
Now, let g0, g1, g2, ..., gK be the number of permutations of length n with number of inversions equal to 0, 1, 2, ..., K.
To complete this step, we can multiply the polynomial g0 + g1x + ... + gKxK by itself (in O(K2) or 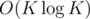 with FFT, but that doesn't really change the complexity since the precomputation already takes O(K2)), to obtain the number of pairs of permutations of {1, 2, ..., n} and {n + 1, n + 2, ..., 2n} with total number of inversions i for all 0 ≤ i ≤ K.
with FFT, but that doesn't really change the complexity since the precomputation already takes O(K2)), to obtain the number of pairs of permutations of {1, 2, ..., n} and {n + 1, n + 2, ..., 2n} with total number of inversions i for all 0 ≤ i ≤ K.
Next, we just have to multiply this with f(0, 0) + f(1, 1)x + ... + f(K, K)xK and we get the desired answer for permutations of length 2n, as noted above.
Thus, we have found a way to obtain dp[2i][·] from dp[i][·] in O(K2).
To complete the solution, we first write N in its binary representation and compute the dp values for the number formed from the first 10 bits (until the number is greater than K). Then, we can update the dp values when N is multiplied by 2 or increased by 1 in O(K2) time, so we can find the value dp[N][K] in 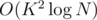 , which fits in the time limit for this subtask.
, which fits in the time limit for this subtask.
Example 2 : Problem Statement in Mandarin
This solution originated from the comment from YuukaKazami here
Problem Statement : A sequence a1, a2, ..., an is valid if all its elements are pairwise distinct and  for all i. We define value(S) of a valid sequence S as the product of its elements. Find the sum of value(S) for all possible valid sequences S, modulo p where p is a prime.
for all i. We define value(S) of a valid sequence S as the product of its elements. Find the sum of value(S) for all possible valid sequences S, modulo p where p is a prime.
Constraints : A, p ≤ 109, n ≤ 500, p > A > n + 1
Firstly, we can ignore the order of the sequence and multiply the answer by n! in the end because the numbers are distinct.
First, we look at the naive solution :
Now, let dp[i][j] be the sum of values of all valid sequences of length j where values from 1 to i inclusive are used.
The recurrence is dp[i][j] = dp[i - 1][j] + i·dp[i - 1][j - 1], depending on whether i is used.
This will give us a complexity of O(An), which is clearly insufficient.
Now, we'll use the idea from the last example. We already know how to calculate dp[i + 1][·] from dp[i][·] in O(n) time. Now, we just have to calculate dp[2i][·] from dp[i][·] fast.
Suppose we want to calculate dp[2A][n]. Then, we consider for all possible a the sum of the values of all sequences where a of the elements are selected from 1, 2, ..., A and the remaining n - a are from i + 1, i + 2, ..., 2A.
Firstly, note that 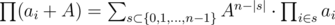 .
.
Now, let ai denote the sum of all values of sequences of length i where elements are chosen from {1, 2, ..., A}, i.e. dp[A][i].
Let bi denote the same value, but the elements are chosen from {A + 1, A + 2, ..., 2A}.
Now, we claim that 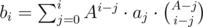 . Indeed, this is just a result of the formula above, where we iterate through all possible subset sizes. Note that the term
. Indeed, this is just a result of the formula above, where we iterate through all possible subset sizes. Note that the term 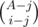 is the number of sets of size i which contains a given subset of size j and all elements are chosen from 1, 2, ..., A. (take a moment to convince yourself about this formula)
is the number of sets of size i which contains a given subset of size j and all elements are chosen from 1, 2, ..., A. (take a moment to convince yourself about this formula)
Now, computing the value of 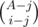 isn't hard (you can write out the binomial coefficient and multiply its term one by one with some precomputation, see the formula in the original pdf if you're stuck), and once you have that, you can calculate the values of bi in O(n2).
isn't hard (you can write out the binomial coefficient and multiply its term one by one with some precomputation, see the formula in the original pdf if you're stuck), and once you have that, you can calculate the values of bi in O(n2).
Finally, with the values of bi, we can calculate dp[2A][·] the same way as the last example, as dp[2A][n] is just 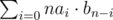 and we can calculate this by multiplying the two polynomials formed by [ai] and [bi]. Thus, the entire step can be done in O(n2).
and we can calculate this by multiplying the two polynomials formed by [ai] and [bi]. Thus, the entire step can be done in O(n2).
Thus, we can calculate dp[2i][·] and dp[i + 1][·] in O(n2) and O(n) respectively from dp[i][·]. Thus, we can write A in binary as in the last example and compute the answers step by step, using at most 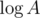 steps. Thus, the total time complexity is
steps. Thus, the total time complexity is  , which can pass.
, which can pass.
This is the end of this post. I hope you benefited from it and please share your own dp tricks in the comments with us.











Thanks for your efforts....A great post indeed!!!
Thanks for great tutorial and here is another problem with Open and Close Interval Trick here is E. Sereja and Intervals.
Thanks. I added it into the post.
open and close trick it would be += v on right hand side in each expression.
You're right. I'll fix it.
Auto comment: topic has been updated by zscoder (previous revision, new revision, compare).
Auto comment: topic has been updated by zscoder (previous revision, new revision, compare).
Thanks...!
This is one of the most useful resources for DP i have come across. Thanks a lot.
Thanks! Can you write about Convex Hull Trick in dp? For example IOI 2016 last task (25 points -> 60 points).
Another example is YATP from NAIPC 2016.
Auto comment: topic has been updated by zscoder (previous revision, new revision, compare).
Hello zscoder, Can you explain this line?
When we add ai, the sum a[i]-a[i-1] will contribute to each of the j open sets, so we increase the current imbalance by j(a[i]-a[i- 1]).
For each currently open set, it's imbalance has been increased by (a[i] - a[i - 1]), since imbalance is defined as maximum of set — minimum of set. (the maximum is increased by a[i] — a[i — 1] now), so the total imbalanced increases by j(a[i] - a[i - 1]).
How can a[i] act as current maximum of many open sets ? Does it not mean that sets will be overlapping ? Actually I am having trouble understanding how imbalance of the new state must be val = k + j(a[i]-a[i-1]) . I understood the a[i]-a[i-1] part but why always multiply with j.
No, the maximum of the open sets might be larger than a[i], but we're assuming they're a[i] for now, and when we go to the next element, if it's still open, we assume it's a[i+1] (and repeat this until it is closed)
Thanks for the article. I just wanted to point out that your solution to Skyscraper looks a lot more complicated than it needs to be. Here is my implementation.
Also some useful post on the topic: http://mirror.codeforces.com/blog/entry/8219 by indy256
for this problem http://mirror.codeforces.com/contest/505/problem/C i didn't get you can you please elaborate it or anyone else
The official tutorial here explains it better. The key is that most of the dp states will never be touched so you can ignore them.
Thanks zscoder This post was really helpful for me. But in the open and close interval trick, i'm confused with the first condition. What do you mean by placing the current item in its own group? Is it a closed group?
You open a new group and close it immediately.
Okay now got it. Thank you :)
Actually The problem form YuukaKazami can be solved by Bernoulli number and cross classification. Thanks for your solution,it helped me a lot.
In "Group project" solution — how big k can be?
It's the maximum allowed total imbalance (
0 ≤ k ≤ 1000) as the input specification states.could someone please explain the idea behind 367E Sereja and Intervals .... the corresponding editorial isn't very helpful
Hi. For the trick "Change the object to dp", shouldn't the number of ways to go from cell (x1, x2) to cell (y1, y2) be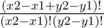 for x2 > x1, y2 > y1 since we have x2 - x1 number of "right arrows" to move along the x-axis and y2 - y1 "up arrows" to go from y1 to y2?
for x2 > x1, y2 > y1 since we have x2 - x1 number of "right arrows" to move along the x-axis and y2 - y1 "up arrows" to go from y1 to y2?
Yes I have the similar doubt. because for a 2*2 grid there are 2 ways to go from cell [1][1] to cell [2][2]. But if we follow the equation provided by zscoder in the post then the answer will be 0 because the upper portion will be (2-1+2-1-2)!-> 0! -> 1 and the lower portion will be (2-1+1)!*(2-1+1)! -> 2!*2!=4. and the answer will be 1/4=0 but this is not correct.
There's another problem that uses Connect Component DP: CEOI16 — Kangaroo
Does anyone have any other problems for CC DP? I'm still pretty weak at it, so I need some more practice.
Can anyone help me how to learn DP?
Maybe the answers to this question on quora may help you by providing some resources.
Could anyone explain me the transitions of DP components technique using in problem CEOI16 — Kangaroo?
I found the code of this and it seems to be so clean and elegant DP but I couldn't understand it ?
Thanks in advanced.
For the solution above, the idea is that $$$dp[i][j]$$$ stores how many ways are there to arrange the first $$$i$$$ numbers into $$$j$$$ components such that within each component, the numbers are alternating. Additionally, we want to impose the additional restriction that in a component, the first number must be less than than the second number, and the last number must be less than the second-to-last number. (This means that $$$(1 3 2)$$$ is allowed as a component, but $$$(1 2)$$$ would not be even though it follows the alternating pattern). We can ignore this restriction for the left side of the component containing the starting number and the right side of the component containing the ending number. The main reason for this restriction is that we will be iterating from $$$i = 1$$$ to $$$i = n$$$ and adding these numbers into components from the previous dp state, so we want to be able to add higher numbers to both ends of a component (except for before the starting number and after the ending number).
The first case ($$$i = 1, j = 1$$$) is just the base case, since there's only one way to put a singular number into a component.
For the second case, this is the case where the number we are trying to add is one of the endpoints. There is only one possible place where a number can go. If it is the starting number, it has to go at the beginning (and it either joins the leftmost component or it creates a new one). The same thing is true for the ending number.
For the last case, the two transitions given are that we merge two components or we create a new one. If we merge two components, then because there are $$$j+1$$$ components, there are $$$j$$$ places where we can add the new element. This new element will then be merged with the components to the left and to the right. For example, if we have $$$(1 3 2)$$$ as one component and $$$(5 6 4)$$$ as another, then we could add $$$7$$$ in the middle to make $$$(1 3 2) 7 (5 6 4)$$$. Then we can also merge both of these together, so we get $$$(1 3 2 7 5 6 4)$$$ as a result. We know that this merging move is always valid because of the additional restriction we added to each component. We could also choose to just create a new component instead of doing any merging. If there are $$$j-1$$$ components currently, then there are $$$j$$$ locations where we could potentially create a new component (though we have to subtract the start and the end if the starting point and ending point have been placed down). There is no transition from $$$dp[i - 1][j]$$$ to $$$dp[i][j]$$$ since adding the new value to only one component breaks that restriction we imposed earlier (for example, $$$(2 3 1)$$$ is a valid component, but both $$$(4 2 3 1)$$$ and $$$(2 3 1 4)$$$ are not.
Thanks so much ! It makes so much sense to me now <3
Thanks for the tutorial! Btw the link with the topcoder tutorial about bits does not work for me. Nevertheless I found the tutorial in this link https://www.topcoder.com/thrive/articles/A%20bit%20of%20fun:%20fun%20with%20bits
another connected component DP problem: 1515E — Phoenix and Computers
editorial doesn't mention anything about this but comments does
In 'Open and Close Interval Trick', I can't understand how this should work
Suppose there are j open sets. When we add a_i, the sum a_i - a_(i-1) will contribute to each of the j open sets, so we increase the current imbalance by j(a_i - a_(i-1)).Let's imagine we have an array [3,5,6,7,8,9,...] and we are applying our DP and now we are on the 6th element (with the value 9) where there are three open intervals which are [3], [5,6,7], [8].
if we add 9 to the first group the imbalance will increase by 9-3 = 6.
if we add 9 to the second group the imbalance will increase by 9-5 = 4.
if we add 9 to the third group the imbalance will increase by 9-8 = 1.
if we add 9 to its own group the imbalance will increase by 9-9 = 0.
As we can see the new value of the imbalance depends on where our current element will be added.
how we can just add
j(a_i - a_(i-1))to the current imbalance which is in the case of our example is 3*(9-8)=3. That doesn't make sense. Any help, pleaaase ??I have the same doubt? Did you understand why?
Hello,I have a question regarding the example for closed and open intervals: In the first and third transitions,why is the new imbalance val instead of k ? Given that we create a new group which at that moment has only the element i in it,that group has the imbalance 0,so the total imbalance increases by 0,and the new imbalance shoud be k.I'd appreciate any insight! Thanks in advance !
Thanks for this post
.