n is a number and n=(p1^c) * (p2^d).Here p1 and p2 are prime. Let a=p1^c and b=p2^d.
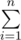 gcd(i,n)=
gcd(i,n)= 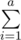 gcd(i,a) *
gcd(i,a) * 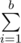 gcd(i,b)
gcd(i,b)
How to prove this? Any explanation? Thanks in advance.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
n is a number and n=(p1^c) * (p2^d).Here p1 and p2 are prime. Let a=p1^c and b=p2^d.
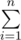 gcd(i,n)=
gcd(i,n)= 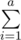 gcd(i,a) *
gcd(i,a) * 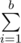 gcd(i,b)
gcd(i,b)
How to prove this? Any explanation? Thanks in advance.
| Name |
|---|



Each divisor of n looks like p1i × p2j. The sum on the right is
(φ(p1a) + p1 + p12 + p13 + ... + p1a) × (φ(p2b) + p2 + p22 + p23 + ... + p2b)
Using CRT you can make a bijection between terms on the right and and i on the left. For example, there are φ(n) values for which gcd(i, n) = 1, and there is φ(p1a)φ(p2b) = φ(n) on the right. Also, you can take φ(p1a) values which are coprime to p and then you can take only one of p2, p22, ... to make i for which gcd(i, n) = p2, or p22, etc.
Please explain briefy. I am too weak in math.