I get an impression that a lot of coders struggle with geometric problems and prefer to avoid them. That's not much of a surprise, considering that I couldn't find a good writing explaining the basics and giving useful advice how to proceed. Moreover, some resources obfuscate this beautiful area to the point it's despised by the readers. I'll try to change that, but first I'll mention some of the better resources:

geomalgorithms.com This is where you can start if you don't have a basic notion of a vector. Also there are more detailed explanations for some examples I'll list, but I dislike the implementations.

This post in Russian has a link to the code that's most similar to mine, with some comments (unfortunately, also is Russian) .

Point structure and operations

Without further ado, I'll start with my code for the Point structure. Explanations are below, so don't rush to dive into the code yourself. I don't like when basic operations take too much space, so formatting is peculiar here. Also I used defines to avoid code repetition. I hope this won't obscure the ideas too much, and I promise the code will get better once we get to non-trivial functions :)

template <class F>
struct Point {
  F x, y;
  Point() : x(0), y(0) {}
  Point(const F& x, const F& y) : x(x), y(y) {}

  void swap(Point& other) { using std::swap; swap(x, other.x); swap(y, other.y); }
  template <class F1> explicit operator Point<F1> () const {
    return Point<F1>(static_cast<F1>(x), static_cast<F1>(y)); }
  template <class F1> Point& operator = (const Point<F1>& other) {
    x = other.x; y = other.y; return *this; }
  template <class F1> Point& operator += (const Point<F1>& other) {
    x += other.x; y += other.y; return *this; }
  template <class F1> Point& operator -= (const Point<F1>& other) {
    x -= other.x; y -= other.y; return *this; }
  template <class F1> Point& operator *= (const F1& factor) {
    x *= factor; y *= factor; return *this; }
  template <class F1> Point& operator /= (const F1& factor) {
    x /= factor; y /= factor; return *this; }
};

template <class F> int read(Point<F>& point) { return read(point.x, point.y) / 2; }
template <class F> int write(const Point<F>& point) { return write(point.x, point.y); }

template <class F> istream& operator >> (istream& is, Point<F>& point) {
  return is >> point.x >> point.y; }
template <class F> ostream& operator << (ostream& os, const Point<F>& point) {
  return os << point.x << ' ' << point.y; }

template <class F> inline Point<F> makePoint(const F& x, const F& y) { return Point<F>(x, y); }
template <class F> void swap(Point<F>& lhs, Point<F>& rhs) { lhs.swap(rhs); }

#define FUNC1(name, arg, expr) \
template <class F> inline auto name(const arg) -> decltype(expr) { return expr; }
#define FUNC2(name, arg1, arg2, expr) \
template <class F1, class F2> \
inline auto name(const arg1, const arg2) -> decltype(expr) { return expr; }
#define FUNC3(name, arg1, arg2, arg3, expr) \
template <class F1, class F2, class F3> \
inline auto name(const arg1, const arg2, const arg3) -> decltype(expr) { return expr; }

FUNC1(operator -, Point<F>& point, makePoint(-point.x, -point.y))
FUNC2(operator +, Point<F1>& lhs, Point<F2>& rhs, makePoint(lhs.x + rhs.x, lhs.y + rhs.y))
FUNC2(operator -, Point<F1>& lhs, Point<F2>& rhs, makePoint(lhs.x - rhs.x, lhs.y - rhs.y))
FUNC2(operator *, F1& factor, Point<F2>& rhs, makePoint(factor * rhs.x, factor * rhs.y))
FUNC2(operator *, Point<F1>& lhs, F2& factor, makePoint(lhs.x * factor, lhs.y * factor))
FUNC2(operator /, Point<F1>& lhs, F2& factor, makePoint(lhs.x / factor, lhs.y / factor))

FUNC2(operator *, Point<F1>& lhs, Point<F2>& rhs, lhs.x * rhs.x + lhs.y * rhs.y)
FUNC2(operator ^, Point<F1>& lhs, Point<F2>& rhs, lhs.x * rhs.y - lhs.y * rhs.x)

// < 0 if rhs <- lhs counter-clockwise, 0 if collinear, > 0 if clockwise.
FUNC2(ccw, Point<F1>& lhs, Point<F2>& rhs, rhs ^ lhs)
FUNC3(ccw, Point<F1>& lhs, Point<F2>& rhs, Point<F3>& origin, ccw(lhs - origin, rhs - origin))

FUNC2(operator ==, Point<F1>& lhs, Point<F2>& rhs, lhs.x == rhs.x && lhs.y == rhs.y)
FUNC2(operator !=, Point<F1>& lhs, Point<F2>& rhs, !(lhs == rhs))

FUNC2(operator <, Point<F1>& lhs, Point<F2>& rhs,
    lhs.y < rhs.y || (lhs.y == rhs.y && lhs.x < rhs.x))
FUNC2(operator >, Point<F1>& lhs, Point<F2>& rhs, rhs < lhs)
FUNC2(operator <=, Point<F1>& lhs, Point<F2>& rhs, !(lhs > rhs))
FUNC2(operator >=, Point<F1>& lhs, Point<F2>& rhs, !(lhs < rhs))

// Angles and rotations (counter-clockwise).
FUNC1(angle, Point<F>& point, atan2(point.y, point.x))
FUNC2(angle, Point<F1>& lhs, Point<F2>& rhs, atan2(lhs ^ rhs, lhs * rhs))
FUNC3(angle, Point<F1>& lhs, Point<F2>& rhs, Point<F3>& origin,
      angle(lhs - origin, rhs - origin))
FUNC3(rotate, Point<F1>& point, F2& angleSin, F3& angleCos,
      makePoint(angleCos * point.x - angleSin * point.y,
                angleSin * point.x + angleCos * point.y))
FUNC2(rotate, Point<F1>& point, F2& angle, rotate(point, sin(angle), cos(angle)))
FUNC3(rotate, Point<F1>& point, F2& angle, Point<F3>& origin,
      origin + rotate(point - origin, angle))
FUNC1(perp, Point<F>& point, makePoint(-point.y, point.x))

// Distances.
FUNC1(abs, Point<F>& point, point * point)
FUNC1(norm, Point<F>& point, sqrt(abs(point)))
FUNC2(dist, Point<F1>& lhs, Point<F2>& rhs, norm(lhs - rhs))
FUNC2(dist2, Point<F1>& lhs, Point<F2>& rhs, abs(lhs - rhs))
FUNC2(bisector, Point<F1>& lhs, Point<F2>& rhs, lhs * norm(rhs) + rhs * norm(lhs))

#undef FUNC1
#undef FUNC2
#undef FUNC3

Point structure will represent points as well as vectors. Point (x, y) can be viewed as a vector from the origin (0, 0) to (x, y), so there's no point to distinguish this notions. And the name vector is already (inappropriately) taken in C++.

Point was made a template for two reasons:

1. I like templates. And I'm sure I'm not the first one who thought about writing such template, so probably I can save some effort for somebody.
2. If the input coordinates are integer, most computations can be done in integers, but the result may be real (for example, in line intersection, as we'll see later). So, it's useful to have different point types in one program. And here's the first advice: do computations in integers as long as possible, for two obvious reasons:

• they are faster;
• they avoid precision issues.

For example, if you need to find the maximum distance between a pair of points and the coordinates are integer, compute and compare squared distances (that are also integer), and take square root only when you output the result. If you need to sort points by angle, it doesn't mean you have to compute the angles, you'll see other ways soon. You'll be surprised how much can be done without resorting to doubles.

To be fair, recently I found out that double performs better than long long under MSVS compiler on Timus, but only if simple operations like +, -, * are used. So, let me rephrase the advice: avoid using floating point division, square root, and especially trigonometric functions as much as possible.

Wait, doubles should be compared with epsilon, you might recall. How do I reckon with this in my template code? Fret not, my crestfallen readers, for I have a wrapper around floating point types to do that :) If it's easier for you, feel free to strip all the templates and insert epsilons like it's done in the code I linked above.

OK, enough talking about the concept, let's get to implementation. Point contains two fields x and y with obvious meaning, some utility methods including type conversion and basic vector operations. Next, there are I/O functions, where read/write are used in my custom I/O, and more vector operations like addition and multiplication by a scalar. Trailing return type syntax is used to be able to combine points of different types just like primitive built-in types. Now we get to the most important part, operators * and ^ (these symbols were selected solely for historical reasons). They both can be expressed using vector coordinates (the formulas written in the code) and using vector lengths and the angle between them.

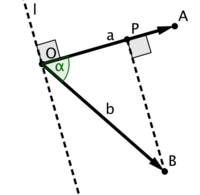
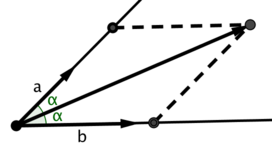
Dot product: a * b = x_ax_b + y_ay_b = |a||b|cos α.
To explain its meaning, lets draw dashed line l perpendicular to the vector a.
Cosine properties apply that:
- if a * b > 0, then b points to the same side of l as a (as in the picture);
- if a * b = 0, then b is collinear with l, so it's perpendicular to a;
- if a * b < 0, then b points to the opposite side of l from a.
To sum it up, dot product sign indicates whether two vectors point in about the same direction.
Now let's look at the absolute value. |b||cos α| = |OP| — the projection of b onto a.
So, the dot product's absolute value is the projection length of b onto a times the length of a.
Nothing special, just remember that we can find projection length and angle cosine from it.

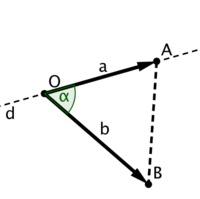
2D cross product: a ^ b = x_ay_b - y_ax_b = |a||b|sin α.
This name is not canon, but I didn't find a better one.
Again, for clarity we draw a line, but this time dashed line d through the vector a.
Sine properties apply that:
- if a ^ b > 0, then b points to the left side of d if we're looking in the direction of a;
- if a ^ b = 0, then b lies on d, so it's collinear with a;
- if a ^ b < 0, then b points to the right side of d (as in the picture).
To sum it up, 2D cross product indicates whether the shortest turn from a to b is in the counter-clockwise direction.
The following function ccw emphasizes this meaning. It acts like a comparator returning negative value if OA goes before OB in the counter-clockwise ordering (the commonly used ordering) and positive value if after. Origin O is (0, 0) by default. If you're having trouble remembering which sign to use, draw vectors a = (1, 0) and b = (0, 1), then it's easy to compute that a ^ b = 1.
The absolute value is very important here, because it's equal to the doubled area of triangle OAB. Together with the sign, we get oriented area, because it changes sign to opposite if we take two vectors in the different order.

Another important property of these operations is that they are linear with respect to both arguments, dot product is symmetric, while cross product is anti-symmetric, thus:

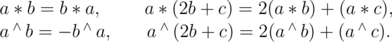
I tried to do my best to explain these operations. Make sure you understand dot and 2D cross product. They are the main building blocks for all the computational geometry algorithms, one cannot understate their importance. I hope the examples below will help you with that.

Next, I have comparison operators, similar to standard pair. It's not substantial which coordinate to compare first, I'll explain later why I chose y.

The following functions deal with rotations and, following my advice, shouldn't be used unless you really have to. angle taking one argument finds the polar angle of the vector, other versions find the angle between two vectors (α in the pictures above). They are based on the following equations, but avoid special cases when denominator is equal to 0:

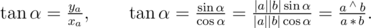
Rotation is performed in the counter-clockwise direction using the well-known formula

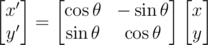
There's one special case of rotation presented in function perp, which returns vector, perpendicular to the given, by rotating by π / 2.

The last section contains functions to find vector length norm (norm is a more mathematical word for vector length), squared length abs, and distance between two points. With vector length defined, it's easy to find the bisector of the angle between two vectors. Recall that two vectors' sum is the diagonal of parallelogram built on these vectors. If we multiply each vector by the length of the other vector, their length will be equal, and the parallelogram will become a rhombus, where diagonal is also the angle bisector.

We've finished with the basic point and vector operations, and here's the next advice. Never access point coordinates directly. Absolutely everything you need can be done using operations we already defined. If you stop thinking in terms of coordinates, and learn to apply operations appropriately, it will become much easier to solve harder problems. You may resort to coordinate access only when you're experienced at geometry, for optimization purposes.

Examples

In order to apply our knowledge, let's first define the Line structure. Here, the question arises: which line representation to use? The standard widely used equation is written as Ax + By + C = 0, but I strongly prefer the parametric equation 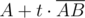, where A is a point on the line, 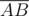is the line direction vector, and parameter t takes any real value. The reasons why it's better:

• it stays the same in higher dimensions;
• it's easily modified to represent a segment by restricting t to [0, 1], or a ray by taking t ≥ 0;
• it promotes the geometric view of the problem, while the standard one is more algebraic and usually leads to more formulas writing instead of coming up with a clean idea.

Most problems have points as an input, so you're free to choose the line equation type. Unfortunately, there are some wicked problems that force you to use the standard equation, so it's better to familiarize yourself with it as well. But we'll proceed with parametric one, implemented in the Line structure:

template <class F>
struct Line {
  Point<F> a, ab;
  Line() : a(), ab() {}
  Line(const Point<F>& a, const Point<F>& b, bool twoPoints = true)
    : a(a), ab(twoPoints ? b - a : b) {}
  Line(const F& xa, const F& ya, const F& xb, const F& yb)
    : a(xa, ya), ab(xb - xa, yb - ya) {}

  void swap(Line& other) { using std::swap; swap(a, other.a); swap(ab, other.ab); }
  template <class F1> explicit operator Line<F1> () const {
    return Line<F1>(Point<F1>(a), Point<F1>(ab), false); }
  template <class F1> Line& operator = (const Line<F1>& other) {
    a = other.a; ab = other.ab; return *this; }

  Point<F> b() const { return a + ab; }
  operator bool () const { return ab != Point<F>(); }
};

template <class F> int read(Line<F>& line) {
  int res = read(line.a, line.ab) / 2;
  return line.ab -= line.a, res;
}

template <class F>
inline Line<F> makeLine(const Point<F>& a, const Point<F>& b, bool twoPoints = true) {
  return Line<F>(a, b, twoPoints);
}

template <class F> void swap(Line<F>& lhs, Line<F>& rhs) { lhs.swap(rhs); }

The first problem that comes into mind is to check whether the given point lies on the line. 2D cross product can check for vectors collinearity, we already have line direction vector, and we can connect the given point to any point on the line (we use line.a because it's already computed) to get the second vector. Note that I handle degenerate case when line shrinks to a point in most functions.

template <class F1, class F2>
bool onLine(const Point<F1>& point, const Line<F2>& line) {
  if (!line) return point == line.a;
  return ((point - line.a) ^ line.ab) == 0;
}

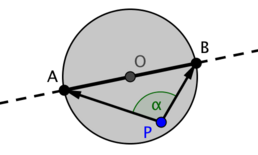
More interesting question is whether the point lies on the segment. We represent a segment by the same Line structure assuming it stores the endpoints. The first part is to check whether the point lies on the line. It doesn't matter which vectors to use as long as they connect the given point and two points on the line. The second condition with scalar product looks very simple, but what it actually checks is whether the point lies inside the disk built on the segment as a diameter. That's because cos α ≤ 0 when , and from the properties of inscribed angles this sets a disk. Line and disk intersection is exactly the segment we were interested in.

template <class F1, class F2>
bool onSegment(const Point<F1>& point, const Line<F2>& seg) {
  if (!seg) return point == seg.a;
  auto vecta = seg.a - point, vectb = seg.b() - point;
  return (vecta ^ vectb) == 0 && (vecta * vectb) <= 0;
}

Moving by increasing difficulty, next we compute some distances. Distance to the line is the length of perpendicular, or the height of triangle (for example triangle ABP₁ in the picture below). We know how to find triangle area using vector coordinates, on the other hand this area is equal to . Thus, the height is the doubled area divided by the base length.

template <class F1, class F2> using distF = decltype(sqrt(F1() + F2()));

template <class F1, class F2>
distF<F1, F2> distLine(const Point<F1>& point, const Line<F2>& line) {
  if (!line) return dist(point, line.a);
  return abs((point - line.a) ^ line.ab) / norm(line.ab);
}

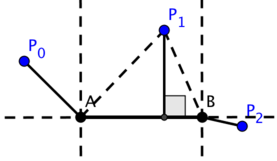
If we have a segment, the base of the perpendicular lies inside this segment only if the given point lies between two perpendicular lines through the segment endpoints. Otherwise, the closest point is one of the endpoints. The picture demonstrates 3 cases we have, and it should be clear that scalar product is exactly the tool we need to distinguish these cases.

template <class F1, class F2>
distF<F1, F2> distSegment(const Point<F1>& point, const Line<F2>& seg) {
  if (((point - seg.a) * seg.ab) <= 0) return dist(point, seg.a);
  if (((point - seg.b()) * seg.ab) >= 0) return dist(point, seg.b());
  return distLine(point, seg);
}

In order to find not just the distance, but the projection point itself, let's recall that we can find projection length with the correct sign using the scalar product: (a * b) / |a|. All we have to do next is to scale the line direction vector to match this length, we get (notation from the last picture is used):

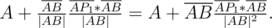
Reflection then can be found using the fact that the projection is the midpoint of the segment connecting the point and its reflection.

Note that the following functions use division to compute the result. Even if all the input coordinates are integer, the output may be real. To enforce the correct type conversion, the output variable is passed by reference and should have the desired floating point type.

template <class F1, class F2, class F3>
void projection(const Point<F1>& point, const Line<F2>& line, Point<F3>& res) {
  res = line.a;
  if (line) res += line.ab * static_cast<F3>((point - line.a) * line.ab) / abs(line.ab);
}

template <class F1, class F2, class F3>
void reflection(const Point<F1>& point, const Line<F2>& line, Point<F3>& res) {
  projection(point, line, res);
  res = 2 * res - point;
}

Closest point on the segment to the given point is found going through the same 3 cases as with the distance:

template <class F1, class F2, class F3>
void closest(const Point<F1>& point, const Line<F2>& seg, Point<F3>& res) {
  if (((point - seg.a) * seg.ab) <= 0) res = seg.a;
  else if (((point - seg.b()) * seg.ab) >= 0) res = seg.b();
  else projection(point, seg, res);
}

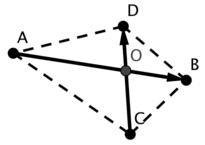
Now we get to the problem I rarely see coded in the best way: line intersection.
First, we assume that lines don't coincide, so the parallel lines never intersect, or we just don't care about such case (and it's often true in practice).
Every point on line AB is represented as 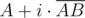, and it lies on line CD when 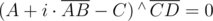. Using linearity, we can solve this equation and get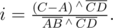
Similarly, for a point 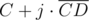that also lies on line AB, we get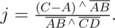
Note that both denominators are equal, and they become zero when lines are parallel, but we assumed in this case lines don't intersect. If the denominator is not zero, we just substitute i in 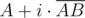with a value we found and get the intersection point, that is unique.

We're done with line intersection, but what if we need to intersect segments? Intersection point may lie on a line, but not on a segment, in which case we should indicate no intersection. Fortunately, we already have expressions for i and j, and we need to check that 0 ≤ i ≤ 1 and 0 ≤ j ≤ 1. Instead of doing floating point comparisons, we can check 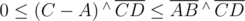(if the denominator is positive), and similar inequality for j. Because we may need to intersect any combination of open/closed segments, rays and lines, I made a template checker. For example, to intersect a ray with an open segment, call intersectLines<1, 0, 2, 2>(...).

Exercise: it's easy to see that numerators of i and j are the doubled areas of triangles ACD and ACB respectively. Prove, that denominator is the doubled area of quadrilateral ACBD.

template <int TYPE> struct EndpointChecker {};
template <> struct EndpointChecker<0> {  // no endpoint (ray)
  template <class F> bool operator ()(const F& a, const F& b) const { return true; }};
template <> struct EndpointChecker<1> {  // closed endpoint
  template <class F> bool operator ()(const F& a, const F& b) const { return a <= b; }};
template <> struct EndpointChecker<2> {  // open endpoint
  template <class F> bool operator ()(const F& a, const F& b) const { return a < b; }};

template <int LA, int LB, int RA, int RB, class F1, class F2, class F3>
bool intersectLines(const Line<F1>& lhs, const Line<F2>& rhs, Point<F3>& res) {
  assert(lhs && rhs);
  auto s = lhs.ab ^ rhs.ab;
  if (s == 0) return false;
  auto ls = (rhs.a - lhs.a) ^ rhs.ab;
  auto rs = (rhs.a - lhs.a) ^ lhs.ab;
  if (s < 0) s = -s, ls = -ls, rs = -rs;
  bool intersect =
    EndpointChecker<LA>()(decltype(ls)(0), ls) && EndpointChecker<LB>()(ls, s) &&
    EndpointChecker<RA>()(decltype(rs)(0), rs) && EndpointChecker<RB>()(rs, s);
  if (intersect) res = lhs.a + lhs.ab * static_cast<F3>(ls) / s;
  return intersect;
}

template <class F1, class F2, class F3>
bool intersectClosedSegments(const Line<F1>& lhs, const Line<F2>& rhs, Point<F3>& res) {
  return intersectLines<1, 1, 1, 1>(lhs, rhs, res);
}

Now, we'll consider closed segment intersection when lines can coincide. The code remains the same, except for s == 0 case.
First, we check that segments lie on the same line, not on different parallel lines: ls != 0.
Intersection of two segments on 1D line is the segment between their maximum left endpoint and minimum right endpoint. operator < we defined introduces strict ordering on any 2D line, so we can apply the solution from 1D case to find the intersection.

template <class F1, class F2, class F3>
bool intersectSegments(const Line<F1>& lhs, const Line<F2>& rhs, Line<F3>& res) {
  auto s = lhs.ab ^ rhs.ab;
  auto ls = (rhs.a - lhs.a) ^ rhs.ab;
  if (s == 0) {
    if (ls != 0) return false;
    auto lhsa = lhs.a, lhsb = lhs.b();
    auto rhsa = rhs.a, rhsb = rhs.b();
    if (lhsa > lhsb) swap(lhsa, lhsb);
    if (rhsa > rhsb) swap(rhsa, rhsb);
    res = Line<F3>(max(lhsa, rhsa), min(lhsb, rhsb));
    return res.ab >= Point<F3>();
  }
  auto rs = (rhs.a - lhs.a) ^ lhs.ab;
  if (s < 0) s = -s, ls = -ls, rs = -rs;
  bool intersect = 0 <= ls && ls <= s && 0 <= rs && rs <= s;
  if (intersect)
    res = Line<F3>(lhs.a + lhs.ab * static_cast<F3>(ls) / s, Point<F3>());
  return intersect;
}

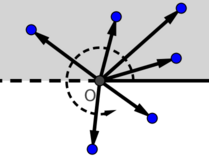
Remember I promised you to show point sorting by polar angle? The time hast cometh! We will sort the points around the given origin using the predicate ccw. One doesn't simply apply it when the points are all around the origin. For example, two points on one line with the origin, but to the different sides of it will be considered equal. Therefore, first we partition the plane in two halves using operator >: one above the origin including horizontal ray to the right (greyed out part), one below including horizontal ray to the left. The shortest rotation angle between two points in one half also lies in that half, so we can sort them separately with the ccw predicate.

This example is the reason why I compare two points by y first. Polar angle is counted starting with the positive direction of x-axis. So, I need to divide the plane into upper and lower halves, not left and right that comparison by x would produce.

Since we need to know the origin when comparing two points, the comparison cannot be done with a simple function, we need a comparator structure. The implementation actually has two partition calls. Think why the first one is necessary (it separates points that coincide with the origin).

template <class F>
struct AngleCompare {
  const Point<F> origin;
  const bool zero;

  AngleCompare(const Point<F>& origin = Point<F>())
    : origin(origin), zero(origin == Point<F>()) {}

  template <class F1, class F2>
  bool operator () (const Point<F1>& lhs, const Point<F2>& rhs) const {
    return zero ? ccw(lhs, rhs) < 0 : ccw(lhs, rhs, origin) < 0;
  }
};

template <class Iterator, class F>
void sortByAngle(Iterator first, Iterator last, const Point<F>& origin) {
  first = partition(first, last, [&origin](const decltype(*first)& point) {
    return point == origin; });
  auto pivot = partition(first, last, [&origin](const decltype(*first)& point) {
    return point > origin; });
  AngleCompare<F> acmp(origin);
  sort(first, pivot, acmp);
  sort(pivot, last, acmp);
}

Coordinates range

One important detail to discuss is what data type to use, whether in Point template, or your own more specific implementation. Usually, each coordinate's absolute value is limited by 10⁹. Operations that significantly increase this value are those performing multiplication: *, ^, dist2. In all the examples above, and in most other cases, we apply these operations to at most the difference of two input points. Basically, the largest number we can end up with is the squared distance between points ( - 10⁹,  - 10⁹) and (10⁹, 10⁹), which is 8·10¹⁸, and it fits into long long. So, you should be fine if you perform all the multiplications in long long type. If the input or the output is real, don't forget to convert to double or long double when necessary.

Practice

Theory knowledge is worth nothing without practice, so you should go out there and solve problems! To start with, I recommend this training contest. It incorporates most of the examples I provided. I didn't analyze any problems with rays, so you'll have to modify the code to work with them. It's easy, but I believe it helps to improve geometry understanding. There are also problems comprising standard line equation, and after solving them you'll know everything you need about this equation. The statements are in Russian, but they are very concise and get straight to the point, so any modern translator should handle them with ease.