Google APAC 2017 — Round E

8 years ago, # |

← Rev. 3 →

Problem A:

len is length of S.

let count(k) be the number of blue bulbs in range [1, k].

then the answer is count(J) — count(I — 1).

count(k) = count(k % len) + (k / len) * count(len)

for k <= len, we can store the answer in a table.

time complexity O(len)

→ Reply

8 years ago, # |

← Rev. 5 →

-7

EDIT1: Here is the AC code. I have completely avoided overflows as I find f(b) ≥ 0 or not cleverly.(Not using log but finding the GP sum in O(log(VAL)) and returning when sum reaches ≥ 10¹⁸

For Problem B, for given number N, you need to find the smallest number b such that there exists some x so that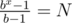 $\text{[math]}$ . Iterate x from 64 to 2 inclusive, and binary search for value of b.
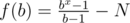Consider $\text{[math]}$ . This will be an non-decreasing function. So binary search for the value of b that makes it 0.
*Warning: Beware of overflows. See implementation above.

→ Reply

ammunation

8 years ago, # ^ |

Why is x from [2,18] ? Suppose , for N=1125899906842623 , the value of x should be 50 for b=2. Please correct me if I'm mistaken. I did the same thing as you explained where x iterated from [2,70]. Although I was getting overflow for the large inputs. Can you please elaborate on how to solve it using log.

→ Reply

8 years ago, # ^ |

← Rev. 2 →

-6

Why would be x from [2, 18]? You are right. It won't be. It would be from [2, 64].

Regarding usage of log:
You know you are in trouble when b^x is very lagre or (b - 1) * N is very large. How to check whether x * y ≥ 10¹⁸? Simple log(x) + log(y) ≥ 18. So whenever you are in trouble, you know that result is very large. So you can use log(x) = log(x + 1).
Finally checking whether f(b) is > or < 0 becomes easy when integer overflow is occurring. You need to check sign of (log(b^x - 1) - log(N) - log(b - 1)).

→ Reply

Inactivated

8 years ago, # ^ |

we can avoid using log, we can just iterate for all the bases within 10⁶ upto all powers such that highest power is less than 10¹⁸ , Now if the base is bigger than 10⁶ then then number n must have less than 3 bits in its representation .Now we just have to check if 1 +x +x² = n . This is equivalent to saying that n-1 is product of 2 consecutive numbers , which we can easily check . Also if we need to check x*y>10¹⁸, we can check without using log using this : x >= 10¹⁸ / y.

→ Reply

8 years ago, # ^ |

"upto all powers such that highest power is less than 10¹⁸?" I don't think so because limit on b^x is N * (b - 1) and N itself can be 10¹⁸.
For product of two no's, yes you are right.

→ Reply

Inactivated

8 years ago, # ^ |

← Rev. 2 →

we'll keep adding along the powers to form the possible numbers . hence although the limit on b^x is N * (b - 1) but on the whole number n the limit is 10¹⁸ ,we only need to check the highest power less than 10¹⁸

→ Reply

sam29

8 years ago, # ^ |

← Rev. 2 →

Yup I don't think you need to use log. I have provided a function below that will generate all the numbers that can be represented by a particular base.

void f2(ll base)
{
	ll val=0;
	ll num=1;
	while(val <= 1e18 and num<=(LLONG_MAX/base)){
		val+=num;
		a[base].insert(val);
		num*=base;
	}
	val+=num;
	a[base].insert(val);
}

→ Reply

8 years ago, # ^ |

Seems you are right. I have updated the post and attached the code.

→ Reply

8 years ago, # ^ |

Hey, Could you link me to your program?
I'm not sure how to implement the binary search as well as how to handle large numbers.(I did read your other comment,but I'm still not sure)

→ Reply

8 years ago, # ^ |

You can see it here.

→ Reply

8 years ago, # ^ |

I somehow managed to pass small but not large in B, and I had already taken care of overflow but it seems that overflow is the only possible issue.

I coded something like this: http://pastebin.com/8Y33HnTZ

and handle if cnt != bit_length (ie sz) and tt != x. No idea where did I fuck up.

→ Reply

thedark

8 years ago, # ^ |

Hey rachit, I used the same technique as yours in contest but is failing for large case Could you please see what is the problem in this code — https://paste.ubuntu.com/23440777/

→ Reply

8 years ago, # ^ |

Yes. I have updated your code. Problem was in expo function. :)

→ Reply

thedark

8 years ago, # ^ |

Thanks very much, made very silly mistake :(

→ Reply

y119777

8 years ago, # ^ |

← Rev. 3 →

for length x, we need to find b satisfy the condition, for N , the most significant bit is b^(x — 1), b is the only one could be result, so, we can get it by b = pow(N, 1.0 / (x — 1)), if b > 1,then we just need to check whether length x of base of b is the ans. i learn it from hdu_toraoh.sorry for my poor english.

→ Reply

8 years ago, # |

← Rev. 8 →

Problem B:

for B in range(1, N):

     binary search for nr_digit in range(2, 64), s.t. N has nr_digits "1" in base B

just iterator over B and nr_digit is also fine...

trick : use a multiprecision library to deal with large integer, like boost::multiprecision::mpz_int. It's allowed in codejam.

UPD: It's wrong. I didn't remember it clearly until I looked at my code... see comments below.

→ Reply

rahulkhairwar

8 years ago, # ^ |

This is what I was doing but it didn't give a solution to a single test case in 3-4 minutes.

→ Reply

8 years ago, # ^ |

I'm wrong. I iterator over nr_digit first, then binary search for B.

So I did the same thing as rachitiitr.

link to my code http://ideone.com/pSMiap

many tricks...

→ Reply

8 years ago, # |

← Rev. 6 →

Problem C: count the number of tuple (a, b, c, x) s.t.

(1) D divides x

(2) a >= 1, b >= 0, c >= 0

(3) a * x + b * (x + 1) + c * (x + 2) == N

for x = D; x <= N; x += D do

    for a = 1; a * x <= N; ++a do

         count number of (b, c) by solving indefinite equation.

time complexity O(N / D * N), but you have 4min to solve the problem. it's enough...

→ Reply

8 years ago, # ^ |

What would be the solution for the large input?

→ Reply

8 years ago, # ^ |

← Rev. 2 →

This is the solution to the large input.

It takes me about 10 seconds to process the large input.

A program that executes 10^11 instructions is acceptable in Google codejam.

→ Reply

8 years ago, # ^ |

I tried implementing what you said but its taking very long.
I think I am doing this part wrong:
count number of (b, c) by solving indefinite equation
Could you show me your code or tell me the correct way of counting?
Sorry if its a dumb question.

→ Reply

8 years ago, # ^ |

← Rev. 2 →

For this problem, we need to find (b, c) s.t.

b * (x + 1) + c * (x + 2) = R

because -(x + 3) * (x + 1) + (x + 2) * (x + 2) = 1.

a solution is (b, c) = (R * (-x-3), R * (x + 2))

all solutions are (b, c) = (R * (-x-3) + k * (x + 2), R * (x + 2) - k * (x + 1))

the number of solutions is the number of k that makes b >= 0 && c >= 0.

This link may be usefull : http://math.stackexchange.com/questions/20717/how-to-find-solutions-of-linear-diophantine-ax-by-c

→ Reply

8 years ago, # ^ |

Generally, we can get initial solution and incremental of it by extended Euclid algorithm.

→ Reply

8 years ago, # ^ |

← Rev. 2 →

Thanks a lot! Finally got AC and more importantly, learnt something very useful and important today!

→ Reply

8 years ago, # ^ |

Here's an O(NT) solution.

iterate through the possible amount of buckets from 1 to floor(N/D)
calculate the amount of balls on the leftmost bucket, this is fixed unless D=1, which could be handled by considering two values for the leftmost bucket.
Note that we only care about the amount of bucket that has the same amount of balls with the leftmost one. This is because the sequence is non-decreasing and maximum difference is two so there is only one partition method for each amount of buckets that shares the same value with the leftmost one.

Code: http://pastebin.com/G5Mmzfdw

→ Reply

8 years ago, # ^ |

It's a very insightful observation.

x is fixed can be proved in another way.

(a + b + c) x <= (a + b + c) x + b + 2 c < (a + b + c)(x + 2)

then

N / (a + b + c) -2 <= x < N / (a + b + c)

so the range of x under fixed (a + b + c) is at most 2. x is fixed if D > 1.

→ Reply

infomaniac

8 years ago, # ^ |

← Rev. 3 →

Thanks ! That helped a lot !

→ Reply

infomaniac

8 years ago, # ^ |

I did not look at your code because I want to understand it conceptually first. So basically in addendum to Georeth's formulation, you are fixing a first right ? Conceptually how is this fixing b and c or the number of valid b and c ?

→ Reply

8 years ago, # ^ |

This is because I have also fixed [a+b+c] (the total amount of buckets). Therefore if I also fix [a], [b+c] is fixed. That will form a system of two unknowns with two variables, and obviously that will result in only one valid answer set. Also, since the range of [b+c] is continuous, the range of [a] is also continuous and we can make use of this to calculate the range of [a] and the total amount of valid answers in O(1).

→ Reply

infomaniac

8 years ago, # ^ |

Woah! That was a very elegant way of doing this !

→ Reply

8 years ago, # ^ |

Ikr, I wouldn't have thought of this hadn't I misread the statement as solving the question for given N,D and fixed bucket amount. =]

→ Reply