i4018's blog

Fast and reliable bipartite matching code
By i4018, history, 8 years ago, In English

i'm looking for a well written, bug-free and fast code for the 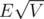bipartite matching algorithm. can anyone share your code please?

  • Vote: I like it
  • +6
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it +13 Vote: I do not like it

Not my code but I think this is pretty good: http://zobayer.blogspot.com/2010/05/maximum-matching.html

→ Reply
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

thanks.

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I want to share my version of bipartite matching, in the hope that, if it is wrong on certain test cases, someone would notice. It is not conventional, in the sense that the "Match" function has one loop instead of two. I have never noticed any notable difference, and the code is pretty short and encapsulated.

https://github.com/bicsi/code_snippets/blob/master/bipartite_match.cpp

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +8 Vote: I do not like it

    Your implementation is O(VE) (and it is called Kuhn matching if I am not mistaken)

    Do you have AC on these problems with this code?

    http://www.spoj.com/problems/MATCHING/

    http://mirror.codeforces.com/contest/722/problem/D

    The last one it is intended to be greedy, but I got TLE with Kuhn and AC with Hopcroft-Karp

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Both problems got accepted, without any substantial modifications to the algorithm. Link to the CF problem: http://mirror.codeforces.com/contest/722/submission/22865806

      However, it seems that having the two "parts" of the bipartite graph swapped, I was getting TLE. Probably because at the same number of iterations, I was doing O(n * log(n)) work going through the bigger part, rather than O(n).

      EDIT: It seems that a simple test comparing the two versions on the number of iteration of the outer loop on random test cases would easily prove / disprove the algorithm. I am, however, too lazy to do that right now :).

      → Reply